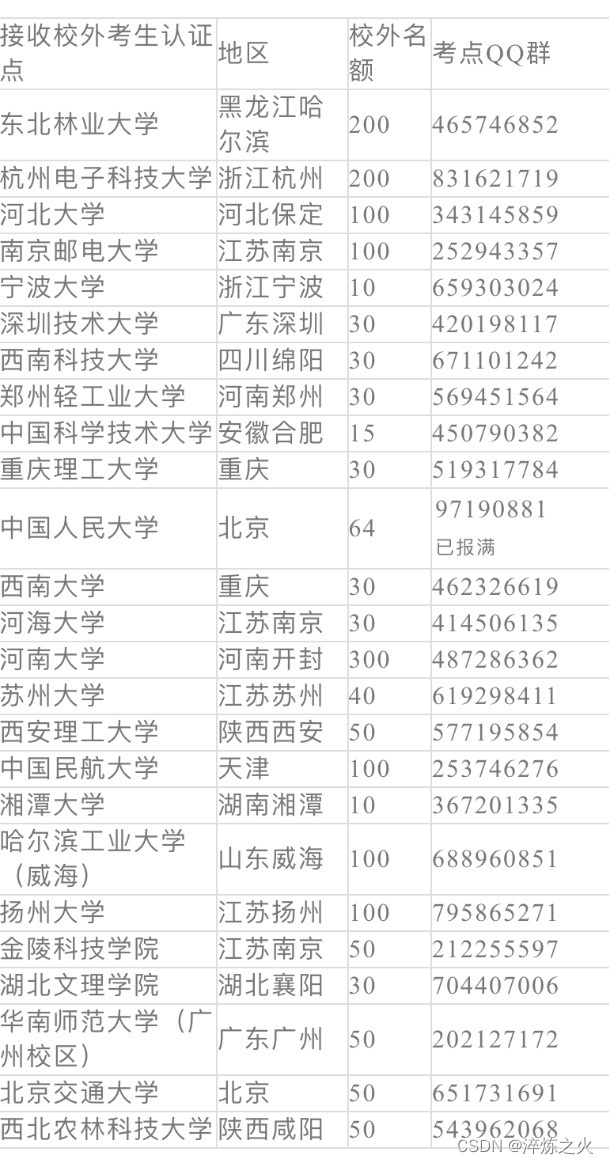
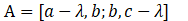题目

http://118.190.20.162/home.page

T1 现值计算

思路

根据题意第$k$年的$x$元的当前价值为$x\times (1+i{)}^{-k}$计算各个价值，最后求和。

代码

int main() {int n; double i;scanf("%d %lf", &n, &i);i += 1;double x = 0, y, z;for (int k = 0; k <= n; k++) {scanf("%lf", &y);z = 1;for (int j = 0; j < k; j++) {z *= i;}x += (1.0 / z) * y;}printf("%f", x);return 0;
}

T2 训练计划

思路

dp，设项目耗时为$c(i)$，
科目$i$的最早开始时间为：
$$a(i)=a(p_i)+c(p_i)$$
其中$a(i)$初始化为1，最早可以从第1天开始训练。
科目$i$的最晚开始时间为
$$b(i)=mi{n}_{p_u=i}(b(u)-c(u))$$
其中$b(i)$初始化为$n+1-c(i)$，这样保证最后一天完成所有训练。
若存在$b(i)<1$，则顿顿无法$n$天内完成所有训练。
题目约束科目最多只有一个依赖，这样的图是森林，实际上，可以推广到DAG图上。

代码

vector<int> q[105];
int a[105], b[105], c[105], g[105];
// 最早开始时间：所有先行项目完成的时间+1
// 最晚开始时间：所有后续项目所需的时间-1void solve() {int n, m, x;cin >> n >> m;for (int i = 1; i <= m; i++) {cin >> x;if (x) {g[i] = x, q[x].push_back(i);}   // 有x后续项目i(一个或多个)a[i] = 1;   // 所有项目最早可以在第1天开始}for (int i = 1; i <= m; i++) {cin >> c[i];b[i] = n - c[i] + 1;}for (int i = 1; i <= m; i++) {if (!q[i].empty()) {for (int k = 0; k < q[i].size(); k++) {a[q[i][k]] = a[i] + c[i];}}}bool ok = 1;for (int i = m; i >= 0; i--) {if (g[i]) {b[g[i]] = min(b[g[i]], b[i] - c[g[i]]);if (b[g[i]] < 1) { ok = 0; break; }}}for (int i = 1; i <= m; i++) cout << a[i] << " ";if (ok) {cout << '\n';for (int i = 1; i <= m; i++) cout << b[i] << " ";}
}

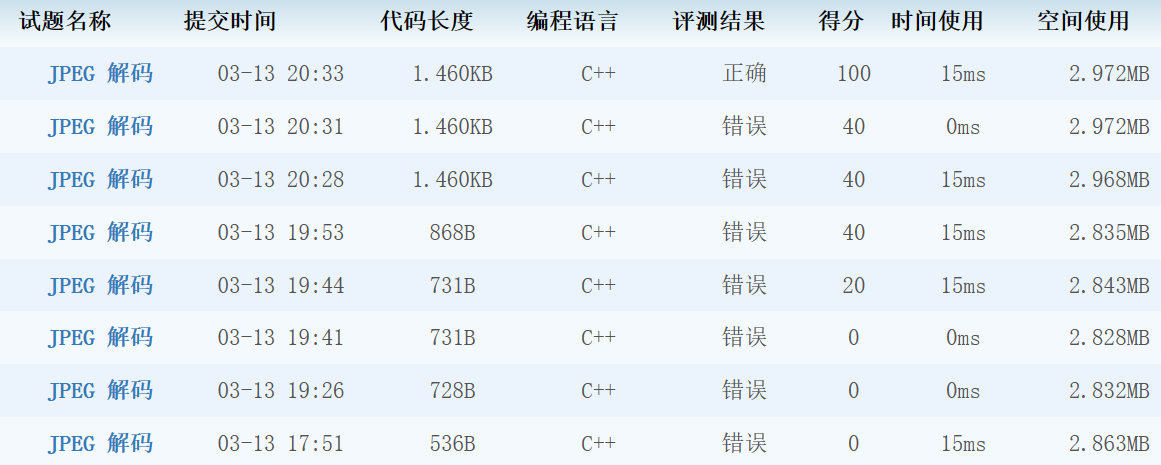
T3 JPEG 解码

思路

根据问题描述模拟：

3. Z字形扫描，只有$8\times 8$的大小，很多方法都可以，观察到在没有矩阵的内部（而不是在边缘），扫描遵循$(x,y)$均$+1,-1$的规律，维护一个方向变量dir，每次移动$x,y$同时加dir。在矩形的边缘，我是假想它根据方向变量进行扫描，发现出界了，再修正，同时将dir取反。

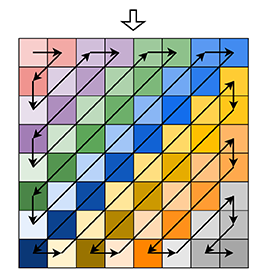
4. 离散余弦变换，根据公式计算，4层的嵌套循环实现。

其他步骤略。

代码

const double pi = acos(-1);int a[10][10], b[10][10];
double c[10][10];void out() {for (int i = 0; i < 8; i++) {for (int j = 0; j < 8; j++) {cout << b[i][j] << ' ';}   cout << '\n';}
}void solve() {for (int i = 0; i < 8; i++) {for (int j = 0; j < 8; j++) {cin >> a[i][j];}}int n, t;cin >> n >> t;int x, y, k; x = y = k = 0;int dir = 1;for (int i = 0; i < n; i++) {cin >> b[x][y];x -= dir; y += dir;if (x < 0 || x > 7 || y < 0 || y > 7) {if (x + y > 7 || (x == 8 && y == -1)) {if (dir > 0) { x += 2, y--; }else x--, y += 2;dir = -dir;}   // (7,0)之后一步进入到另外一半else {// 出界,修正位置，更换方向if (dir > 0) x += dir;else y -= dir;dir = -dir;}}// printf("%d, %d\n", x, y);}if (!t) { out(); return; }for (int i = 0; i < 8; i++) {for (int j = 0; j < 8; j++) {b[i][j] *= a[i][j];}}if (t == 1) { out(); return; }// 离散余弦逆变换for (int i = 0; i < 8; i++) {for (int j = 0; j < 8; j++) {for (int u = 0; u < 8; u++) {for (int v = 0; v < 8; v++) {double au, av;auto get = [&](int k) -> double {if (!k) return sqrt(0.5);else return 1;};au = get(u), av = get(v);c[i][j] += au * av * b[u][v] * cos(pi / 8 * (0.5 + i) * u) * cos(pi / 8 * (0.5 + j) * v);}}c[i][j] *= 0.25;}}// 四舍五入for (int i = 0; i < 8; i++) {for (int j = 0; j < 8; j++) {b[i][j] = (int)(c[i][j] + 128.5);b[i][j] = max(0, b[i][j]);b[i][j] = min(255, b[i][j]);// cout << c[i][j] << ' ';}   // cout << '\n';}out();
}