第28次csp认证T3 JPEG 解码解析

题目说明

问题比较长，就只放个链接吧：http://118.190.20.162/view.page?gpid=T158

经验分享

做这种大模拟的题目，对于经验不是很丰富的新手来说，更应该着眼于得分点，先做那些问题简单、数据规模小的子任务，不断调试，慢慢提高分数。考试基本是不限制提交次数的，如果一次性写完再调试，对于这种复杂的问题来说是一定会有很多出错误的，到时候语法、逻辑等等的失误都不容易被发现，所以最好是写一段小功能就测试一下，确保是正确的再向下进行，先拿到一部分分，不至于最后满盘皆输！针对这个题就需要一步一步对照题目给的数据的矩阵的变化是否正确，最终才更快调试准！

对于此类大模拟题目，问题背景基本可以不看，或者省略着看个大概。重点在于问题描述的输入输出，而且有一定概率完全按照问题描述的步骤去写代码即可得到正确答案，有时还需要选一个复杂度低一些的算法从70分优化到100等等。

题目详解

这个题在csp的第三题里面算是超级简单的一道题了，没有复杂的资源分配和时间逻辑，仅仅是一个jpeg的解码任务，任务明确且难度超级低，因为题目完全说明了步骤，只需要按步骤来做就可以。

真正的难点在于扫描数据的矩阵对应关系和对矩阵进行离散余弦变换。

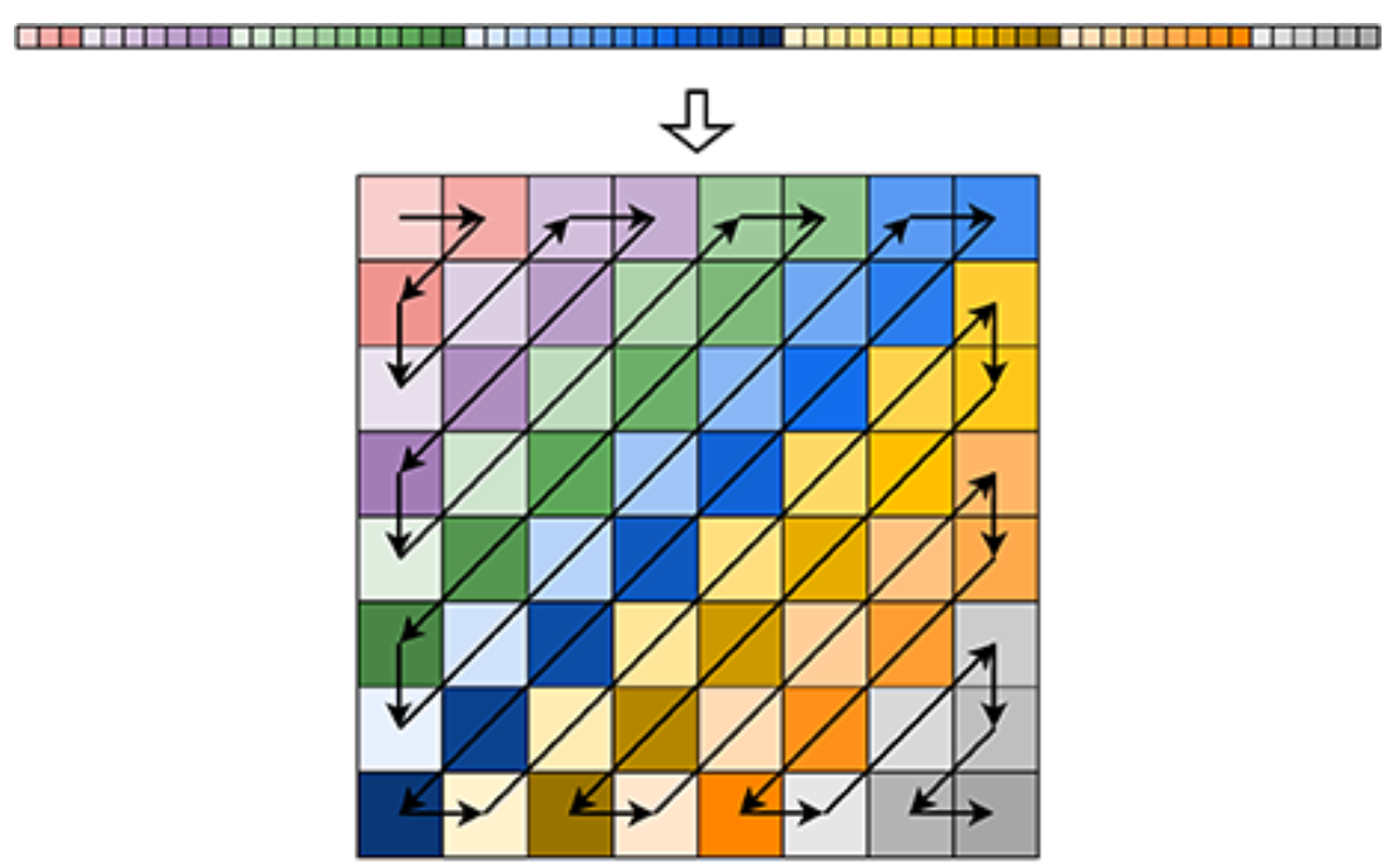
对于前者，只需要确定好矩阵和输入的线性数据的映射关系即可，在这里我用了对角矩阵的映射关系，一种是从左下向右上，一种是从右上向左下。需要讨论i+j为奇数还是偶数的情况去对应上述两种情况，同时还需要注意斜对角超过了中间的斜线后每一条线穿过的小正方形会逐渐减少！也就是需要确定两个公式，下面的公式是通过等差数列求和推导出来的，要小心ij数组下标是从0开始的，以及某些数数中的+1-1问题，需要调试很多次！

一、从左下到右上（i+j是偶数）

i+j<=7的情况：map[i,j]=Line[(i+j)*(i+j+1)/2+j]（就是计算ij这个位置前面的方块个数+j，因为此方向j是从0开始增加的）

i+j>7的情况：map[i,j]=Line[36+(23-i-j)*(-8+i+j)/2+7-i]（就是计算斜对角线前的36个方块+ij这个位置前面的斜对角线后面的方块个数+7-i，因为此方向7-i是从0开始增加的）

二、从右上到左下的情况（i+j是奇数）

i+j<=7的情况：map[i,j]= Line[(i+j)*(i+j+1)/2+i]（思想同上）

i+j>7的情况：map[i,j]=Line[36+ (23-i-j)*(-8+i+j)/2+7-j]（思想同上）

分成上边两种情况再通过i+j是偶数还是奇数就可以用四种情况完成蛇形输入，不需要耗费其他大量代码模拟过程。

对于后者，只需要搞清楚是怎么计算的过程，保存好中间变量去计算就可以了，需要小心的地方也有，比如题目里的1/2，如果代码里也写成1/2，就会按照整数除法而算成0，需要写0.5才能当成double计算，还有开方，acos、cos等计算。

其余的点无非就是模拟，很简单，不再赘述。

满分代码

以下是我的调试过程：

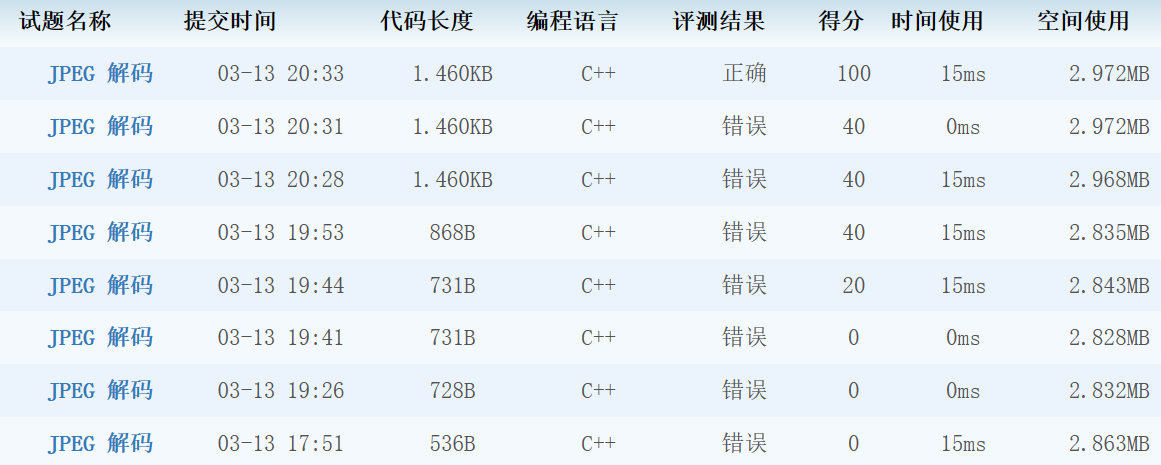
#include<bits/stdc++.h>
using namespace std;int Q[8][8];
double M[8][8];
double MM[8][8];
int n;
int T;
int N[70];
int index;void t0(){for(int i=0;i<8;i++){for(int j=0;j<8;j++){if((i+j)%2==0){//偶数 if(i+j<=7){index = (i+j)*(i+j+1)/2+j;M[i][j] = N[index];}else{index = 36+(23-i-j)*(-8+i+j)/2+7-i;M[i][j] = N[index];}}else{//奇数 if(i+j<=7){index = (i+j)*(i+j+1)/2+i;M[i][j] = N[index];    }else{index =36+ (23-i-j)*(-8+i+j)/2+7-j;M[i][j] = N[index];}}}}
}void t1(){t0();for(int i=0;i<8;i++)for(int j=0;j<8;j++)M[i][j]*=Q[i][j];
}void t2(){t1();for(int i=0;i<8;i++){for(int j=0;j<8;j++){double tempres = 0;for(int u=0;u<8;u++){for(int v=0;v<8;v++){double temptempres = M[u][v];if(u==0) temptempres*=sqrt(0.5);if(v==0) temptempres*=sqrt(0.5);temptempres*=cos(acos(-1)/8*(i+0.5)*u)*cos(acos(-1)/8*(j+0.5)*v);tempres += temptempres;}}MM[i][j] = tempres/4+128;if(MM[i][j]>=255) MM[i][j] = 255;else if(MM[i][j]<=0) MM[i][j] = 0;else MM[i][j] =  round(MM[i][j]);}}for(int i=0;i<8;i++)for(int j=0;j<8;j++)M[i][j] = MM[i][j];
}int main(){for(int i=0;i<8;i++)for(int j=0;j<8;j++)cin>>Q[i][j];cin>>n>>T;for(int i=0;i<n;i++) cin>>N[i];if(T==0) t0();else if(T==1) t1();else if(T==2) t2();for(int i=0;i<8;i++){for(int j=0;j<8;j++){cout<<M[i][j]<<" ";}cout<<endl;}
}