1. 算法原理介绍:
1. Householder变换:

2. Givens变换:

3. 矩阵的QR分解


4. 计算特征值的QR方法

5. 上Hessenberg矩阵方法:

2. 实施过程:
1. 约化过程:
1. Householder变换:

2. Givens变换:
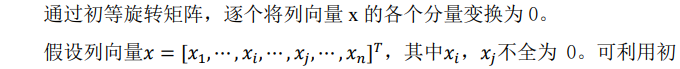
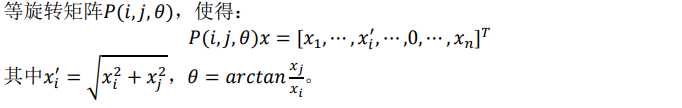
2. 矩阵的QR分解:
1. Householder变换:

2. Givens变换:

3. 计算矩阵特征值的QR方法:

4. 化为上Hessenberg矩阵:

3. 代码实现:
import numpy as np# Householder变换
def householder(x, i=0):x = x.reshape(len(x), 1)ei = np.zeros((len(x), 1))ei[i] = 1y = np.linalg.norm(x, ord=2) * eiif x[i] > 0:w = (x + y) / np.linalg.norm(x + y)else:w = (x - y) / np.linalg.norm(x - y)H = np.eye(len(x)) - 2 * np.dot(w, w.T)return H# Givens变换
def givens(x, i=0):y = np.zeros(x.shape)y[:i + 1] = x[:i + 1]xj = x.copy()dim = len(x)for j in range(i + 1, dim):theta = np.arctan2(xj[j], xj[i])Pi = np.eye(dim)Pi[i, i] = np.cos(theta)Pi[j, j] = Pi[i, i]Pi[i, j] = np.sin(theta)Pi[j, i] = -Pi[i, j]if j == i + 1:P = Pielse:P = np.dot(Pi, P)xj[i] = np.sqrt(xj[i] ** 2 + xj[j] ** 2)y[i] = xj[i]return y, P# QR分解
def QRFact(A, mode):dim = len(A)Ri = A.copy()if mode == 'householder':for i in range(dim - 1):x = Ri[i:, i]Hi = householder(x)Ri[i:, i:] = np.dot(Hi, Ri[i:, i:])Qi = np.eye(dim)Qi[i:, i:] = Hiif i == 0:Q = Qielse:Q = np.dot(Qi, Q)if mode == 'givens':for i in range(dim - 1):x = Ri[:, i]y, Pi = givens(x, i)Ri = np.dot(Pi, Ri)if i == 0:Q = Pielse:Q = np.dot(Pi, Q)D = np.asmatrix(np.diag(np.where(np.diag(Ri) < 0, -1, 1)))R = D * np.asmatrix(Ri)Q = np.asmatrix(Q.T) * D.Ireturn Q, R# 迭代求特征值
def eig_QR(A, mode):Ak = A.copy()flag = 1n = 0eps = 1e-7while flag:Ak0 = Ak.copy()Qk, Rk = QRFact(Ak, mode)Ak = Rk * Qkif (np.sum(np.diag(np.abs(Ak - Ak0))) < eps):flag = 0n = n + 1return np.diag(Ak), n# 化为上Hessenberg矩阵
def Hessenberg(A):dim = len(A)Ri = A.copy()for i in range(1, dim - 1):x = Ri[i:, i - 1]Hi = householder(x)Qi = np.eye(dim)Qi[i:, i:] = Hiif i == 1:Q = Qielse:Q = np.dot(Qi, Q)Ri = np.dot(np.dot(Qi, Ri), Qi)hMat = np.asmatrix(Ri)return hMatif __name__ == '__main__':n = int(input('请输入矩阵阶数:'))A = np.random.randint(0, 10, (n, n))A = A.dot(A.T)eig, n = eig_QR(A, 'givens')print('Givens变换迭代次数为:{}\n求得特征值为:{}'.format(n, eig))hMat = Hessenberg(A)eig, n = eig_QR(hMat, 'householder')print('上Hessenberg矩阵Householder变换迭代次数为:{}\n求得特征值为:{}'.format(n, eig))eigval, vec = np.linalg.eig(A)print('numpy内置函数求得特征值:{}'.format(eigval))4. 数值算例:
以随机生成的30阶的实对称矩阵为例:

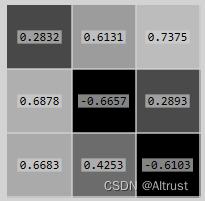



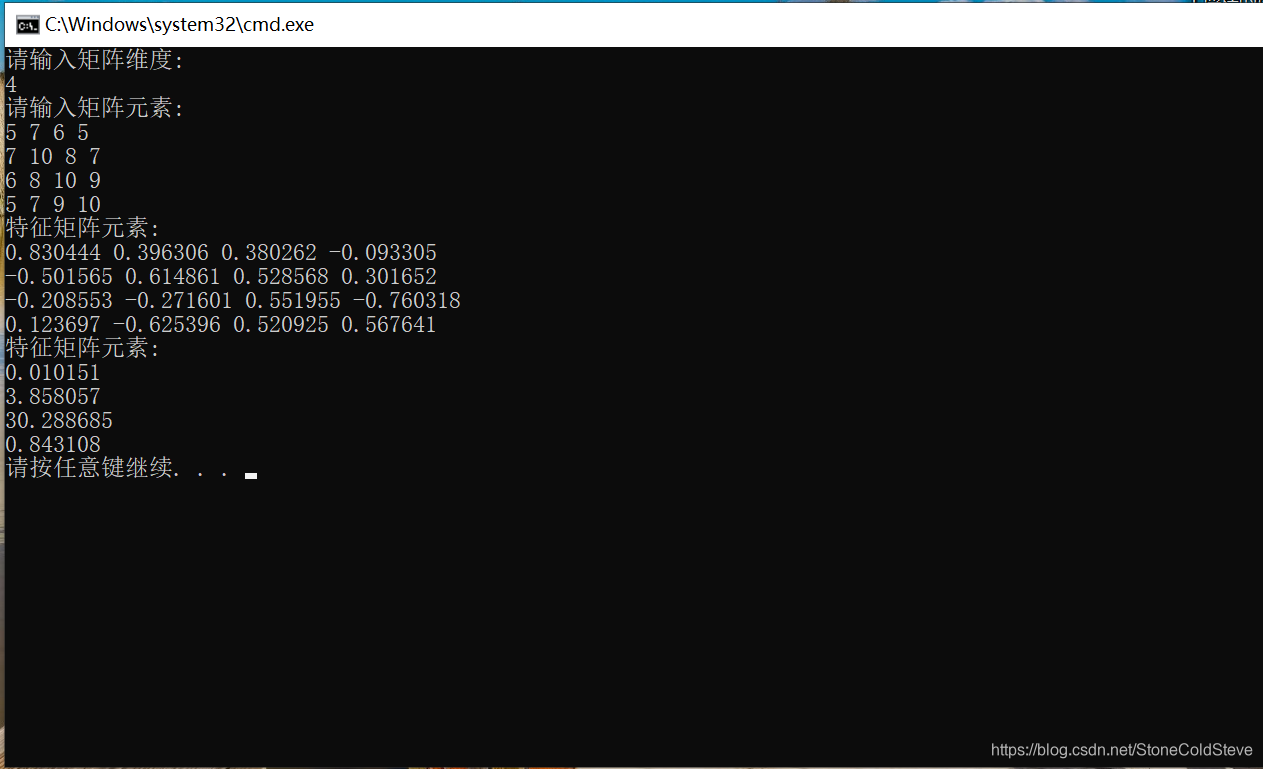




![[IDE]IntelliJ IDEA使用教程(很全)](https://img-blog.csdn.net/20170710160958729)


