1.简介

魔方阵，有时又称幻方或纵横图，由一组排放在正方形中的整数组成，其每行、每列以及两条对角线上的数之和均相等。通常幻方由从1到N*N的连续整数组成，其中N为正方形的行或列的数目。因此 N阶幻方有N行N列，并且所填充的数为从1到N的2次方。

2.分类

分成三类：

奇数阶魔方阵
4M阶魔方阵（其中M为自然数）
4M+2阶魔方阵（其中M为自然数）
(2)和(3)均属于偶数魔方阵

3.排列方法

(1)奇数阶魔方阵

在这里插入图片描述
以三阶为例：
三阶中4和7都是特例对应上述的第五点。

(2)4M阶魔方阵

在这里插入图片描述
当M=1 即n=4时结果如下：

当M=2 即n=8时结果如下：

将对角线连起来，
第一遍填数字从上至下从左到右一次填没有被对角线占的格子（上图为蓝色数字）
第二遍填对角线占的格子从右下角到左上角依次填写（上图为绿色数字)。

(3)4M+2阶魔方阵

在这里插入图片描述
当M=1 即n=6时结果如下：

4.代码表示

(1)奇数魔方阵

三阶为例：

//奇数魔方阵
void Magic1()
{
#define ROW 3              //定义有3行
#define COL ROW            //定义列 等价于：列数=行数assert(ROW % 2 != 0);  //断言列数对2取余不为0 即：列的总数为奇数int arr[ROW][COL] = { 0 };//定义一个二维数组 初值赋值为0int currow = 0;    //定义一个临时行int curcol = COL / 2;//定义一个临时列  为列的一半arr[currow][curcol] = 1;    //按照规则进行编写 第一行最中间的那个数字为1for (int i = 2; i <= ROW * COL; i++)   //通过for循环将2->总数依次存放{if (arr[(currow - 1 + ROW) % ROW][(curcol + 1) % COL] == 0) //按照规律进行判断 当这个数字的上一行下一列为空时 {currow = (currow - 1 + ROW) % ROW;       //这部分就是为了防止越界问题  规律中的上一行curcol = (curcol + 1) % COL;             //同上                        规律中的下一列}else{currow = (currow + 1) % ROW;//如果不为空那么就直接放在上一个数字的下一行即可}arr[currow][curcol] = i;     //把i值赋给二维数组 }for (int i = 0; i < ROW; i++)   //通过for循环来将结果进行打印{for (int j = 0; j < COL; j++){printf("%-3d", arr[i][j]);}printf("\n");}
#undef ROW        //中止宏定义 
#undef COL
}

(2)4M阶魔方阵

以4阶 8阶为例：

//偶数魔方阵 4K（能被4整除）  //4 8 12 16
void Magic2()
{
#define ROW 4
#define COL ROWassert(ROW % 2 == 0 && ROW % 4 == 0);  //来判断是不是4k+2阶的魔方阵 int arr[ROW][COL] = { 0 };//同样先初始化为0int tmp = 1;                               //先对二维数组从1->最后依次按顺序存储for (int i = 0; i < ROW; i++){for (int j = 0; j < COL; j++){arr[i][j] = tmp++;}}int row1 = 0;//主对角线行int col1 = 0;//主对角线列int row2 = 0;//副对角线行int col2 = 0;//副对角线列//总体划分K*K块（i*j）for (int i = 0; i < (ROW / 4); i++)//i指向行{for (int j = 0; j < COL / 4; j++)//j指向列{row1 = 4 * i;col1 = 4 * j;row2 = 4 * i;col2 = 4 * j + 3;for (int k = 0; k < 4; k++){arr[row1][col1] = (ROW * COL + 1) - arr[row1][col1];arr[row2][col2] = (ROW * COL + 1) - arr[row2][col2];//row1++;col1++;row2++;col2--;}}}for (int i = 0; i < ROW; i++){for (int j = 0; j < COL; j++){printf("%-3d", arr[i][j]);}printf("\n");}#undef ROW
#undef COL
}

(3)4M+2阶魔方阵

以六阶为例：

void Magic3()
{
#define ROW 6
#define COL ROWassert(ROW % 2 == 0 && ROW % 4 != 0);int tmp = 0;int arr[ROW][COL] = { 0 };int currow = 0;int curcol = COL / 4;arr[currow][curcol] = 1;//左上角 两个变量用来临时保存行列下标for (int i = 2; i <= ROW * COL / 4; i++){if (arr[(currow - 1 + ROW / 2) % (ROW / 2)][(curcol + 1) % (COL / 2)] == 0){currow = (currow - 1 + ROW / 2) % (ROW / 2);curcol = (curcol + 1) % (COL / 2);}else{currow = (currow + 1) % (ROW / 2);}arr[currow][curcol] = i;}//右下角  currow = ROW / 2;for (int i = 0; i < ROW / 2; i++, currow++) //i和j指向左上角{curcol = COL / 2;for (int j = 0; j < COL / 2; j++, curcol++){arr[currow][curcol] = arr[i][j] + (ROW * COL / 4);}}//右上角currow = 0;for (int i = ROW / 2; i < ROW; i++, currow++) //i和j指向右下角{curcol = COL / 2;for (int j = COL / 2; j < COL; j++, curcol++){arr[currow][curcol] = arr[i][j] + (ROW * COL / 4);}}//左下角currow = ROW / 2;for (int i = 0; i < ROW / 2; i++, currow++) //i和j指向右上角{curcol = 0;for (int j = COL / 2; j < COL; j++, curcol++){arr[currow][curcol] = arr[i][j] + (ROW * COL / 4);}}//2.先改右半边 大于k+2的列  进行上下交换for (int i = 0; i < ROW / 2; i++){for (int j = ROW / 2 + ROW / 4 + 2; j < COL; j++){tmp = arr[i][j];arr[i][j] = arr[i + ROW / 2][j];arr[i + ROW / 2][j] = tmp;}}//交换左半边，两个中心节点tmp = arr[ROW / 4][COL / 4];arr[ROW / 4][COL / 4] = arr[ROW / 4 + ROW / 2][COL / 4];arr[ROW / 4 + ROW / 2][COL / 4] = tmp;//左半边，除（K+1,1）这个点外，小于k+1的列  上下交换for (int i = 0; i < ROW / 2; i++){for (int j = 0; j < COL / 4; j++){if (i == ROW / 4 && j == 0){continue;}tmp = arr[i][j];arr[i][j] = arr[i + ROW / 2][j];arr[i + ROW / 2][j] = tmp;}}for (int i = 0; i < ROW; i++){for (int j = 0; j < COL; j++){printf("%-3d", arr[i][j]);}printf("\n");}
}

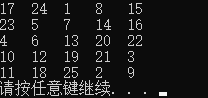
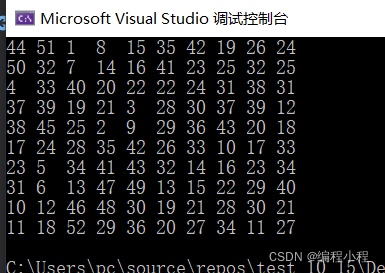
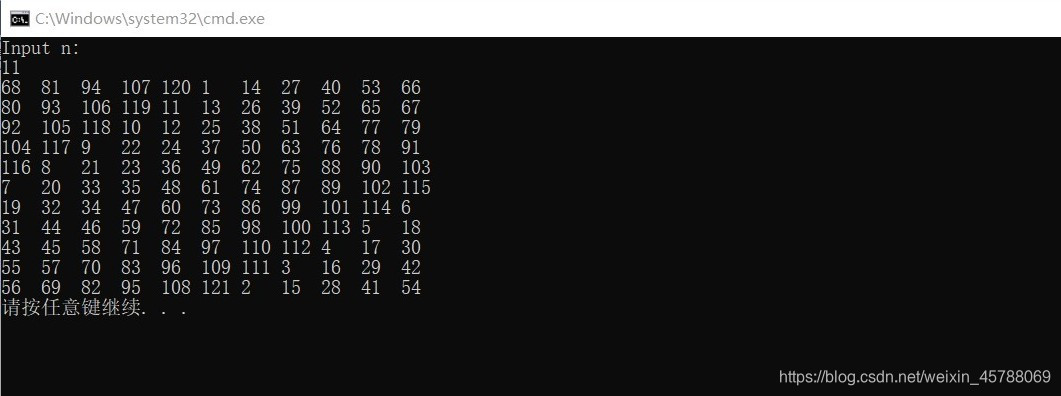
5.运行结果

在这里插入图片描述

6完整代码(供调试)

#include<stdio.h>
#include <assert.h>
#include <stdlib.h>//奇数魔方阵
void Magic1()
{
#define ROW 3              //定义有3行
#define COL ROW            //定义列 等价于：列数=行数assert(ROW % 2 != 0);  //断言列数对2取余不为0 即：列的总数为奇数int arr[ROW][COL] = { 0 };//定义一个二维数组 初值赋值为0int currow = 0;    //定义一个临时行int curcol = COL / 2;//定义一个临时列  为列的一半arr[currow][curcol] = 1;    //按照规则进行编写 第一行最中间的那个数字为1for (int i = 2; i <= ROW * COL; i++)   //通过for循环将2->总数依次存放{if (arr[(currow - 1 + ROW) % ROW][(curcol + 1) % COL] == 0) //按照规律进行判断 当这个数字的上一行下一列为空时 {currow = (currow - 1 + ROW) % ROW;       //这部分就是为了防止越界问题  规律中的上一行curcol = (curcol + 1) % COL;             //同上                        规律中的下一列}else{currow = (currow + 1) % ROW;//如果不为空那么就直接放在上一个数字的下一行即可}arr[currow][curcol] = i;     //把i值赋给二维数组 }for (int i = 0; i < ROW; i++)   //通过for循环来将结果进行打印{for (int j = 0; j < COL; j++){printf("%-3d", arr[i][j]);}printf("\n");}
#undef ROW        //中止宏定义 
#undef COL
}//偶数魔方阵 4K（能被4整除）  //4 8 12 16
void Magic2()
{
#define ROW 4
#define COL ROWassert(ROW % 2 == 0 && ROW % 4 == 0);  //来判断是不是4k+2阶的魔方阵 int arr[ROW][COL] = { 0 };//同样先初始化为0int tmp = 1;                               //先对二维数组从1->最后依次按顺序存储for (int i = 0; i < ROW; i++){for (int j = 0; j < COL; j++){arr[i][j] = tmp++;}}int row1 = 0;//主对角线行int col1 = 0;//主对角线列int row2 = 0;//副对角线行int col2 = 0;//副对角线列//总体划分K*K块（i*j）for (int i = 0; i < (ROW / 4); i++)//i指向行{for (int j = 0; j < COL / 4; j++)//j指向列{row1 = 4 * i;col1 = 4 * j;row2 = 4 * i;col2 = 4 * j + 3;for (int k = 0; k < 4; k++){arr[row1][col1] = (ROW * COL + 1) - arr[row1][col1];arr[row2][col2] = (ROW * COL + 1) - arr[row2][col2];//row1++;col1++;row2++;col2--;}}}for (int i = 0; i < ROW; i++){for (int j = 0; j < COL; j++){printf("%-3d", arr[i][j]);}printf("\n");}#undef ROW
#undef COL
}//偶数魔方阵 4K+2(不能被4整除) 
// 将其划为4个奇数魔方阵，左上角将1~ROW*COL%4，按照奇数魔方阵赋值进去
//上下标记数字进行交换
//标记的规则 1.右半边大于k+2的列（从1开始）
//2.左半边，上下两个块最中心的点进行交换
//3.左半边小于k+1的列（除了上下半边最中心的行的第一列的那个值不用交换（从1开始））
void Magic3()
{
#define ROW 6
#define COL ROWassert(ROW % 2 == 0 && ROW % 4 != 0);int tmp = 0;int arr[ROW][COL] = { 0 };int currow = 0;int curcol = COL / 4;arr[currow][curcol] = 1;//左上角 两个变量用来临时保存行列下标for (int i = 2; i <= ROW * COL / 4; i++){if (arr[(currow - 1 + ROW / 2) % (ROW / 2)][(curcol + 1) % (COL / 2)] == 0){currow = (currow - 1 + ROW / 2) % (ROW / 2);curcol = (curcol + 1) % (COL / 2);}else{currow = (currow + 1) % (ROW / 2);}arr[currow][curcol] = i;}//右下角  currow = ROW / 2;for (int i = 0; i < ROW / 2; i++, currow++) //i和j指向左上角{curcol = COL / 2;for (int j = 0; j < COL / 2; j++, curcol++){arr[currow][curcol] = arr[i][j] + (ROW * COL / 4);}}//右上角currow = 0;for (int i = ROW / 2; i < ROW; i++, currow++) //i和j指向右下角{curcol = COL / 2;for (int j = COL / 2; j < COL; j++, curcol++){arr[currow][curcol] = arr[i][j] + (ROW * COL / 4);}}//左下角currow = ROW / 2;for (int i = 0; i < ROW / 2; i++, currow++) //i和j指向右上角{curcol = 0;for (int j = COL / 2; j < COL; j++, curcol++){arr[currow][curcol] = arr[i][j] + (ROW * COL / 4);}}//2.先改右半边 大于k+2的列  进行上下交换for (int i = 0; i < ROW / 2; i++){for (int j = ROW / 2 + ROW / 4 + 2; j < COL; j++){tmp = arr[i][j];arr[i][j] = arr[i + ROW / 2][j];arr[i + ROW / 2][j] = tmp;}}//交换左半边，两个中心节点tmp = arr[ROW / 4][COL / 4];arr[ROW / 4][COL / 4] = arr[ROW / 4 + ROW / 2][COL / 4];arr[ROW / 4 + ROW / 2][COL / 4] = tmp;//左半边，除（K+1,1）这个点外，小于k+1的列  上下交换for (int i = 0; i < ROW / 2; i++){for (int j = 0; j < COL / 4; j++){if (i == ROW / 4 && j == 0){continue;}tmp = arr[i][j];arr[i][j] = arr[i + ROW / 2][j];arr[i + ROW / 2][j] = tmp;}}for (int i = 0; i < ROW; i++){for (int j = 0; j < COL; j++){printf("%-3d", arr[i][j]);}printf("\n");}
}int main()
{Magic1();printf("\n");Magic2();printf("\n");Magic3();printf("\n");return 0;
}