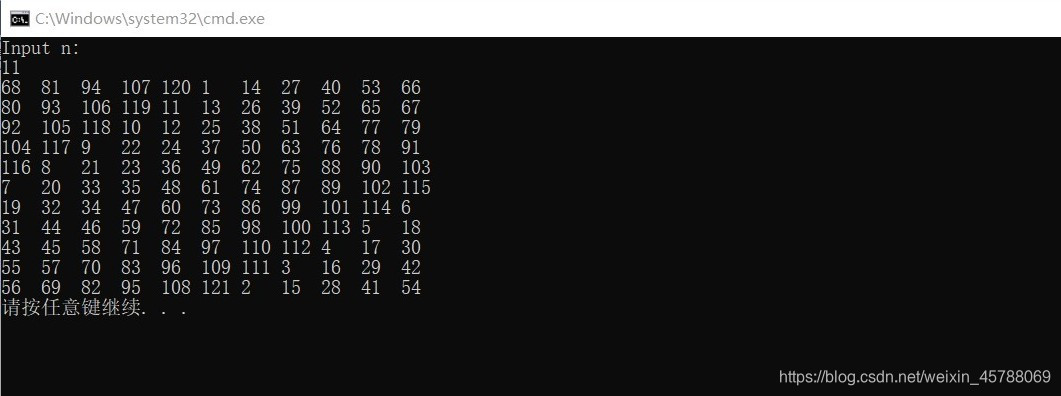
魔方阵的说明：

将1到n(为奇数)的数字排列在n*n的方阵上，且各行、各列与各对角线的和必须相同

此篇文章只讲如何编写奇数阶魔方阵

规律：

⑴ 将1放在第一行中间一列

⑵ 从2开始直到n×n止各数依次按下列规则存放：

    每一个数存放的行比前一个数的行数 -1，列数 +1

⑶ 如果上一个数的行数为1，下一个数的行数应为n，即最后一行 //理解为封闭环形

⑷ 如果上一个数的列数为n，下一个数的列数应为1，即第一列 //理解为封闭环形

⑸ 如果按上面规则确定的位置上已有数，则把下一个数放在上一个数的下面

 具体填数过程：

①  1放在第一行中间

②  2放在1的上一行（即最后一行），下一列

 ③ 3放在2的上一行，下一列（即第一列）

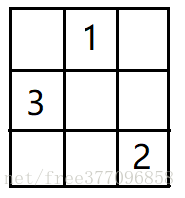
④ 4放在3的上一行，下一列，但该位置被1占据，所以放在3（上一个数）下面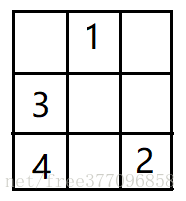

⑤ 5放在4的上一行，下一列，即最中间位置  

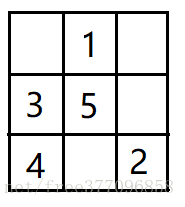
⑥ 6放在5的上一行，下一列

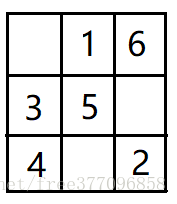
⑦ 7放在6的上一行，下一列，但该位置被4占据，所以放在6（上一个数）下面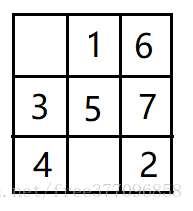

⑧ 8放在7的上一行，下一列

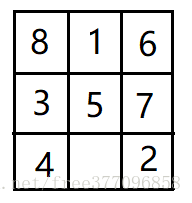
⑨  9放在8的上一行，下一列

 

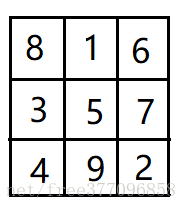
 算法思路：

我们定义一个二维数组arr,进行一个一个数字的填入（上一行后一列的算法）

但是过程中如果下一个填入的位置有数字，我们需要进行判断

为了简便我们一开始就将arr全部初始化为0然后进行填值，后续判断

如果通过上一行后一列的下一个位置不等于0（说明有数字）那么我们就进行下一行同列的算法

上一行后一列： 环形处理  

 当前数的“行”为上一个数 行-1，加上ROW是为了防止出现负数

行： row = (row -1+ ROW) % ROW

当前数的“列”为上一个数 列+1 ，加上ROW是为了防止出现负数

列： col = (col + 1 ) % ROW

如果位置已有数字进行下一行同列：环形处理

 行：row = (row + 2) % ROW
 列：col = (col - 1 + ROW) % ROW

 最好画图理解这几句核心算法

代码示例：

#define ROW 3
int main()
{int arr[ROW][ROW] = {0};//数组初始化全是0 方便后面if语句判断arr[0][ROW/2] = 1;//1放在第一行中间int row = 0;//当前行下标int col = ROW/2;//当前列下标for (int i =2; i <=ROW*ROW; i++) //一个一个数字去填 遍历下标 不是按行列了{//上一行后一列row = (row -1+ ROW) % ROW;   //环形处理col = (col + 1) % ROW;//当前位置有数字有数字if (arr[row][col] != 0){row = (row + 2) % ROW;col = (col - 1 + ROW) % ROW;}arr[row][col] = i;}for (int i = 0; i < ROW; i++){for (int j = 0; j < ROW; j++){printf("%d ", arr[i][j]);}printf("\n");}return 0;
}

程序实现：