镜像下载、域名解析、时间同步请点击 阿里云开源镜像站
将网络上的文件下载到使用 Linux 操作系统的计算机上,需要用到 wget 指令,使用该指令可能会面临两个问题。
首先,如何获取文件的下载 url?这需要你在浏览器上找到要下载文件的链接地址,然后右键 -> 复制链接地址,既可获取该文件的下载 url。以阿里提供的 Centos7 镜像为例,如下图:
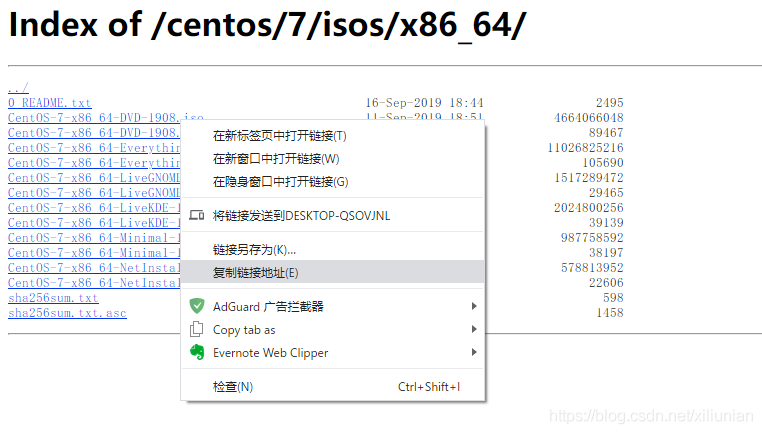
在 Linux 系统上使用 wget 指令即可下载该文件:
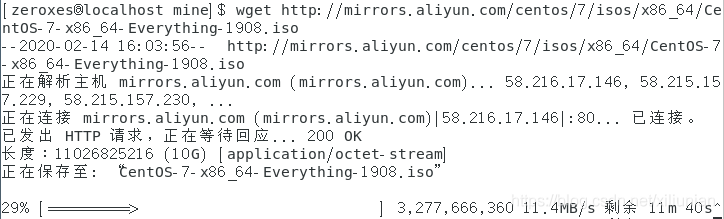
其次,在下载某些文件时,需要通过认证才可以下载,例如在Oracle 的官网上下载JDK8,需要登录之后才可以下载。
在这种情况下,直接右键 -> 复制链接地址,使用获取到的url 是无法下载文件的。此时我们需要先登录通过认证,再通过已经开始下载的文件获取文件的下载 url。如下图所示:
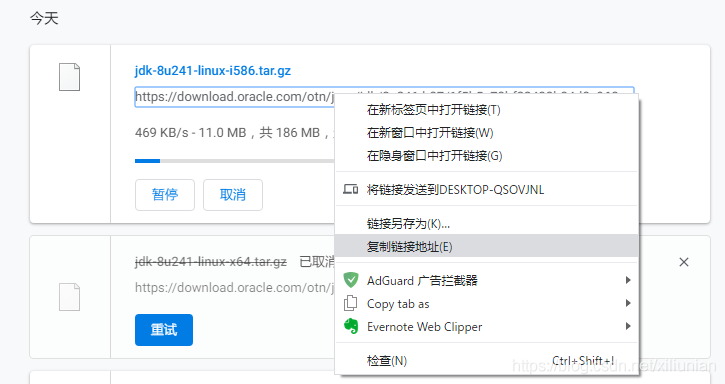
通过该下载 url 可以实现文件下载。如下图:
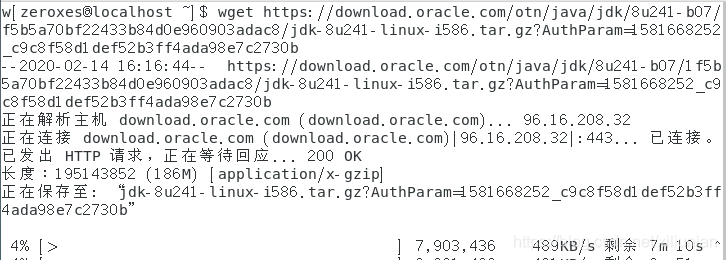
对比下载 Centos7 和 JDK8 的两个下载 url,可以看出二者相差在何处:
Centos7 下载 url:http://mirrors.aliyun.com/centos/7/isos/x86_64/CentOS-7-x86_64-DVD-1908.iso
JDK8 下载 url:https://download.oracle.com/otn/java/jdk/8u241-b07/1f5b5a70bf22433b84d0e960903adac8/jdk-8u241-linux-i586.tar.gzAuthParam=1581668252_c9c8f58d1def52b3ff4ada98e7c2730b
其实需要认证才能下载的文件的下载 url,就是在普通的下载url 的后面加上了一个通过验证之后的参数,JDK8 的下载认证参数为 AuthParam。
不过通常情况下该参数是随机生成的,也有对应的下载时限。对于 JDK8 而言,该下载 url 只有在生成后的5分钟内有效,期间内可以多次下载,超过5分钟再下载则会报错 “ERROR 403:Forbidden”:
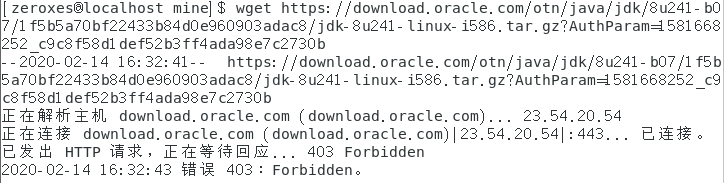
当然如果你觉得这样太麻烦了,也可以先将文件下载到 Windows 系统上,然后借助于 WinScp 将文件上传到 Linux 系统上。
本文转自:https://blog.csdn.net/segegefe/article/details/124289714