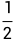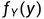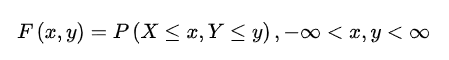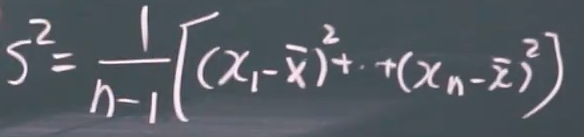概率密度函数
实随机向量的概率密度函数
一个含有m 个随机变量的实值向量
称为mx1实随机向量,或简称随机向量(当维数无关紧要时)。其中,表示样本点,可以是时间,频率,或者位置等。
一个随机向量由它的联合累积分布函数或联合概率密度函数完全描述。一组概率的集合函数
定义为向量x()的联合累积分布函数,简称分布函数。式中,
为实数。
随机向量x()的(联合)概率密度函数定义为
联合概率密度函数的m-1重积分函数
称为随机变量的边缘概率密度函数。
就是说,随机向量x()的联合分布函数等于其联合概率密度函数的积分。
随机变量称为(联合)独立,若对于m个事件
,有以下概率关系成立:
。
复随机向量的概率密度函数
一个复随机变量定义为,其中,
和
分别为实值随机变量。
复随机向量可以表示成
复随机向量的累计分布函数定义为
概率密度函数
累积分布函数是概率密度函数关于所有实部和虚部的2m重积分,即
特别: