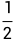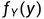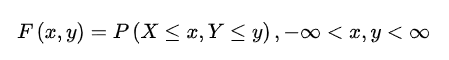如题:2019年10月

分析:概率论是最初要考的一个科目,看了好几遍了吧,总还是没印象。可见别人讲得再天花乱坠,自己不懂,一点用都没有,白白浪费时间。知识,要靠自己去掌握。 还是借此顺下知识点:
答案:详见第5个问题
第一个问题:
何为多维随机变量呢?可以认为是随机变量的叠加。与连续型随机变量一样,其分布函数也是一个平面,只不过个平面是由多条概率密度曲线所围成的。
第二个问题:如何理解二维随机变量分布函数?分布函数对应的就是一个求概率的问题

为什么x>(-∞),y<(+∞)呢???脑补出坐标系就知道了,这表示的就是坐标系的范围。
单独取X或Y的分布函数称为关于X或Y的边缘分布函数。脑补出坐标系就明白了,相当于在x轴或y轴某个点上画线,一条线指定是没有面积的,如何表达面积呢?那就用极限。并且是用趋于正无穷,为什么呢?因为分布函数定义是不大于某个点的概率,-∞表示的比任何数都小的数(这里不能当作一般数来理解,可以当作变量或函数代表趋势),极限是0。+∞表比任何数都大,极限就是无穷。所以负无穷(趋于0)时概率为0,所以只能是趋于正无穷。
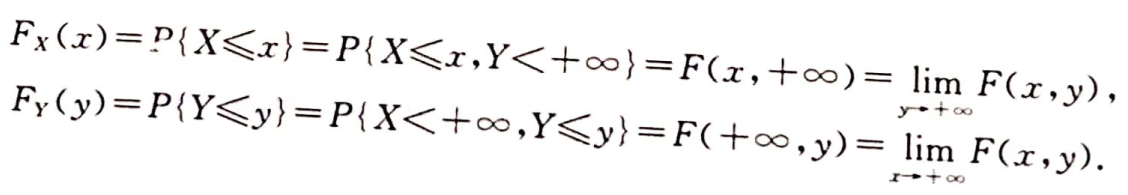
关于矩形区域概率计算理解:
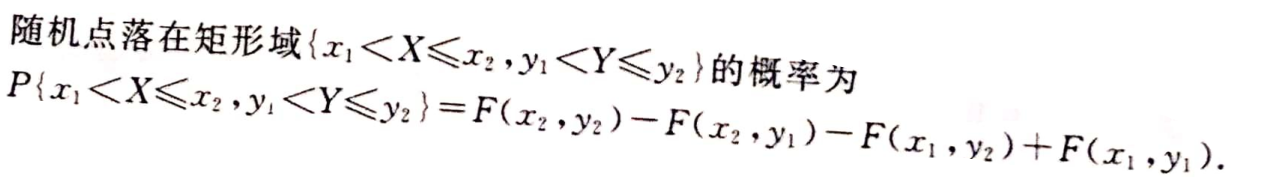
根据分布函数的定义,画个图就知道了,如下:多减了一次F(x1,y1),得加上。
第三个问题:离散型二维随机变量如何理解?
简单来说就是不同坐轴上的两个点,点都是大于0的,这两个点合起来,又对应另一个坐标系的概率值。用两个坐标系可以实现降维。如下图:
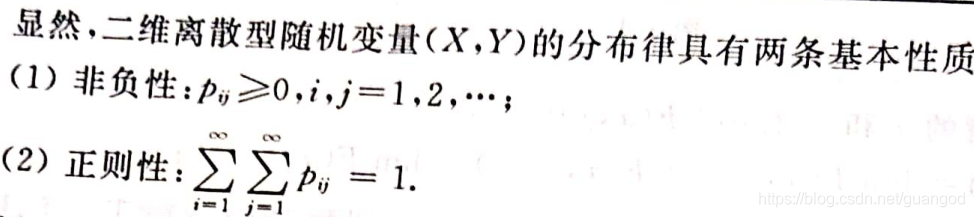
关于二维离散型随机变量的边缘分布律(其分量X、Y各自的分布律):记住下面的表就可以了,Pi.j里的点理解了就可以了,点就代表i或j的所有值域(结果相加)。P.j=1或Pi.=1
第四个问题:二维连续型随机变量之理解?真正的两条曲线围成的面积。这是结论,至于如何理解?还得从二重积分的定义来说起。详见《高等数学复习之二重积分》
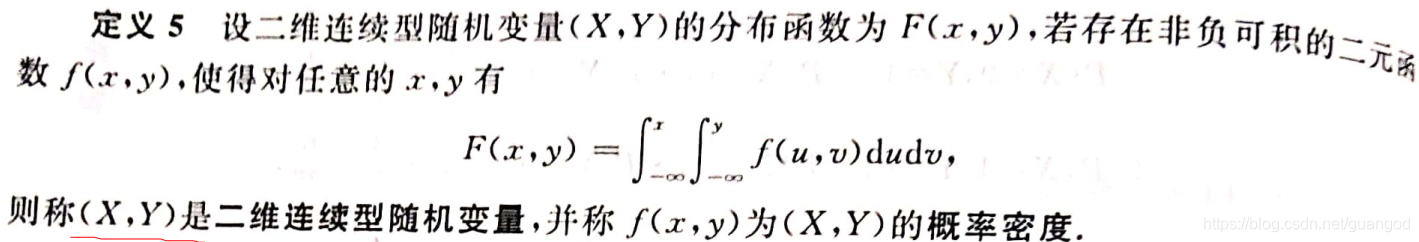
二元函数f(x,y),对应的就是二重积分里面的曲顶函数(或者说是曲顶的边界)。但这里不能当作几何里的概念,就当作一个连续的函数来看,曲定积分的定理可知,连续一定是可积的,也就是说曲顶在坐标系中的面积一定是可以表示的,所以是有别于二重积分的,边界x,y与f(u,v)用的是不同的字母。这里在解题时也要注意一下。
5、二维连续型随机变量的均匀分布本质?????这是曾在《概率论考点之指数分布,泊松分布及积分》关于一维连续型均匀分布时提出的问题。
类似的可以得出就是平行于参考面一个面D,所以概率密度f(x,y)是面积S倒数。书中给出的两种特殊情形:
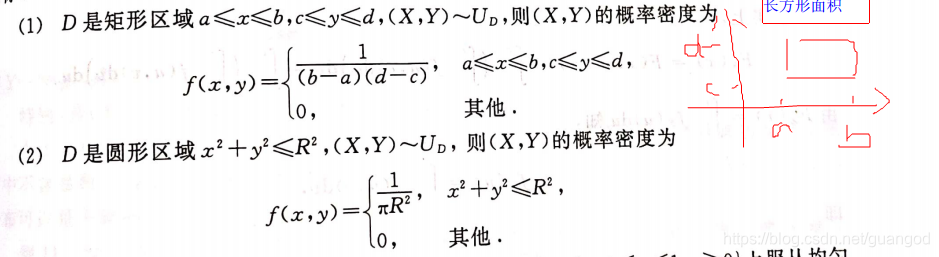
尤其是第一条:当区域是一个矩形时,可以有两个非常重要的结论:x ~ U[a,b],Y ~ U[c,d],分别得出x服从a,b上的均匀分布,Y服从c , d上的均匀分布,并且x,y 相互独立。这个的推导,可以从1、一维连续型概率密度分布本质来推 2、也可以从解定积分的角度来推,其实也很好理解
本题的答案就是考察均匀分布(1)特殊情形:
由题意可知,后面表示区间,x [0,1/2],y [0,1/2],表示的是一个正方形,题目没有明确说概率密度是均匀分布,但只有均匀分布符合题意,其他分布都不符合。根据均匀分布的定义,所以面积的倒数,面积是1/2 x 1/2 =1/4,所以答案是4。
6、二维连续型随机变量正态分布??了解一下,不是考试重点
了解下的符号及其含义:(X,Y)~ N(μ1,μ2,σ1²,σ2²,ρ)
x的数学期望是u1
y的数学期望是u2
x的方差是σ1²
y的方差是σ2²
ρ是相关系数,反映出xy的相关关系
了解下它的图形:
7、关于边缘概率密度???
仔细看了下前面的一维随机变量的内容,还真没有提到过“边缘”之说,最早的是二维离散型随机变量中提到边缘分布律??何为边缘呢?为什么一维中没有边缘之说呢?
根据边缘分布律定义很明显可以得到是分别关于x,y单独的分布律,而一维中只有一个变量,所以用概率密度就可以表示出概率变化趋势,所以没有边缘之说。边缘是针对的多维随机变量而说的,因为具有多个变量,单独研究每个自变量的趋势,就是研究的边缘概率分布规律。
与一维一样,分布律是针对离散的,概率密度才是连续型。所以边缘概率密度的定义如下:

f(x,y);关于x,y的联合密度,在计算时还要掌握边缘密度计算,对y进行积分,那么就把y看作是常数,写成y=f(x)的形式,同时也表示对x轴投影,这与求二重积分是完全一致的。为什么??
脑补一个由两条曲线和两条直线围成的一个面,关于X的边缘密度,可以理解为求x的趋势(也就是x上关于面的上下边界的形状),其实就是确定对x轴投影,穿过的两条上下边界,上下边界的值,其实就针对y的,所以是对y求积分。
同理,对Y求边缘密度,其实是对y上关于面的左右边界的趋势,所以得对y轴投影,左右的趋势值,应该是用x轴上的值来表示,所以是对x求积分。
重要结论: