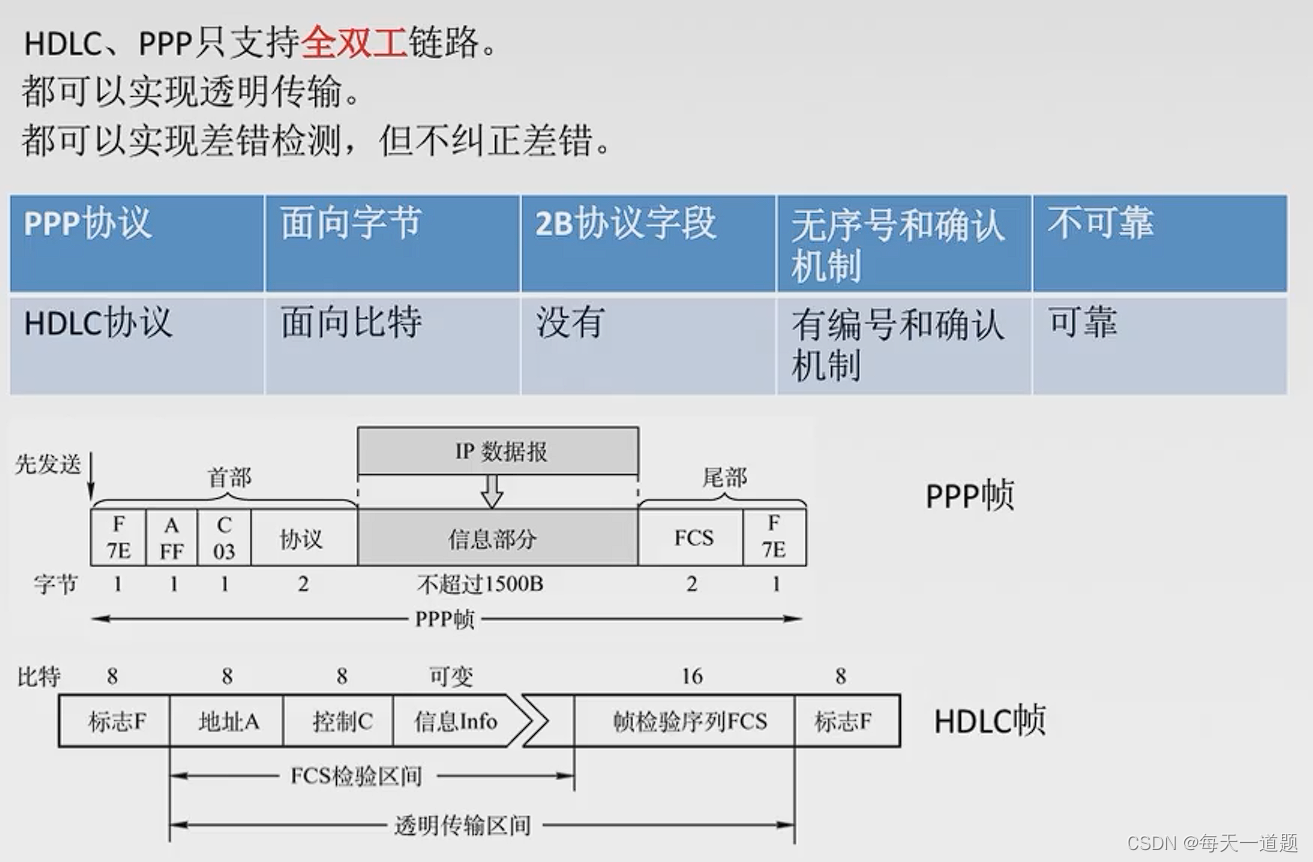
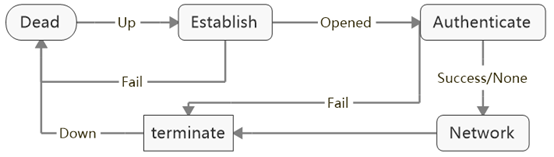
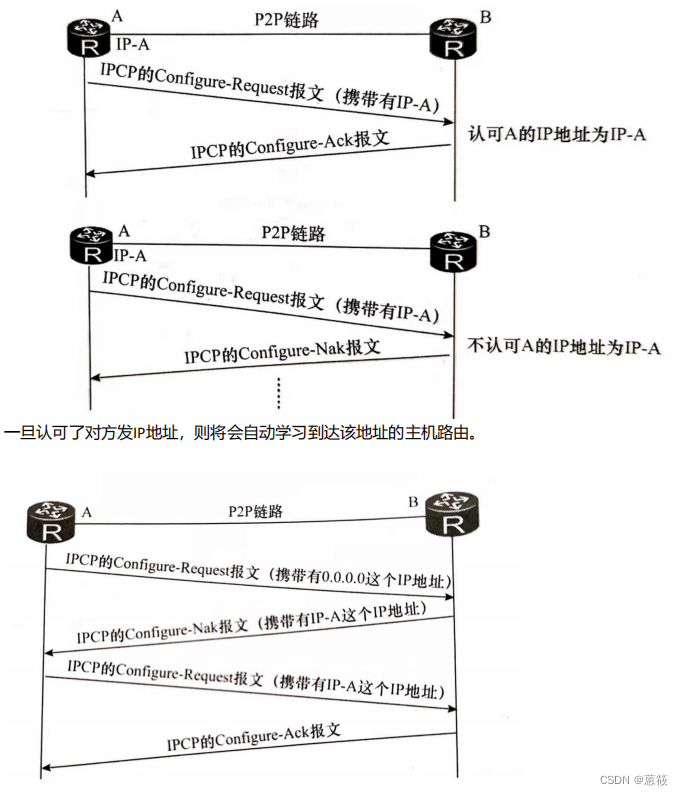
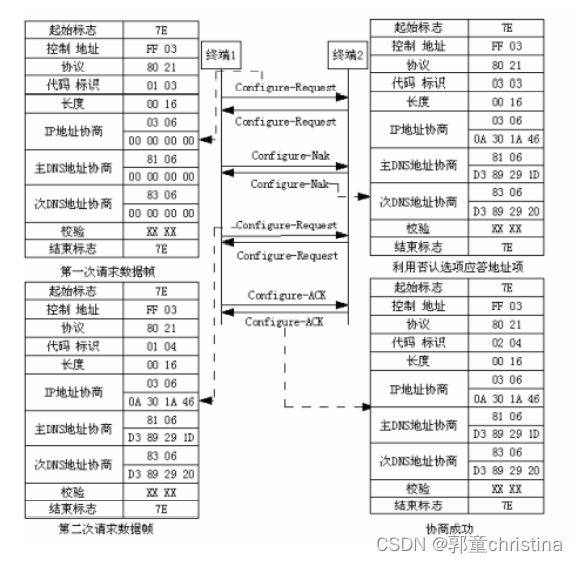
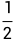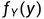这个是quora上的一个回答 What is the difference between probability and likelihood?
在评论中这位老师将概率密度函数和似然函数之间的关系,类比成 2b 和 a2 之间的关系。详细翻译如下:
2我们可以做一个类比,假设一个函数为 ab,这个函数包含两个变量。
如果你令b=2,这样你就得到了一个关于a的二次函数,即 a2 :
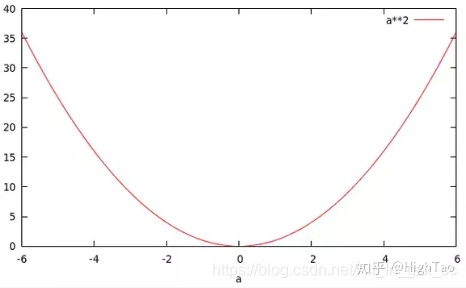
当你令a=2时,你将得到一个关于b的指数函数,即2b :
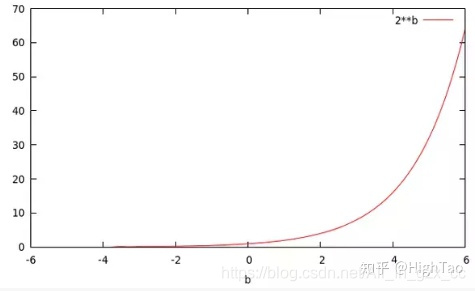
可以看到这两个函数有着不同的名字,却源于同一个函数。而p(x|θ)也是一个有着两个变量的函数。如果,你将θ设为常量,则你会得到一个概率函数(关于x的函数);如果,你将x设为常量你将得到似然函数(关于θ的函数)。
下面举一个例子:有一个硬币,它有θ的概率会正面向上,有1-θ的概率反面向上。θ是存在的,但是你不知道它是多少。为了获得θ的值,你做了一个实验:将硬币抛10次,得到了一个正反序列:x=HHTTHTHHHH。无论θ的值是多少,这个序列的概率值为 θ⋅θ⋅(1-θ)⋅(1-θ)⋅θ⋅(1-θ)⋅θ⋅θ⋅θ⋅θ = θ⁷ (1-θ)³比如,如果θ值为0,则得到这个序列的概率值为0。如果θ值为1/2,概率值为1/1024。但是,我们应该得到一个更大的概率值,所以我们尝试了所有θ可取的值,画出了下图:
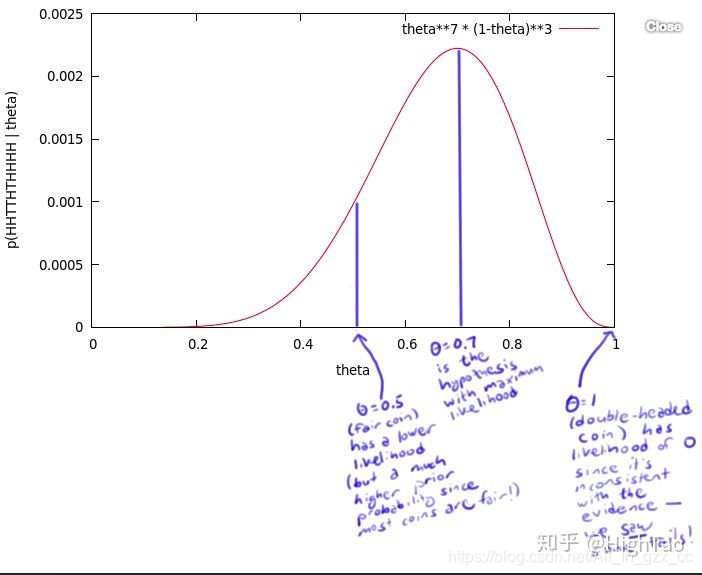
这个曲线就是θ的似然函数,通过了解在某一假设下,已知数据发生的可能性,来评价哪一个假设更接近θ的真实值。如图所示,最有可能的假设是在θ=0.7的时候取到。但是,你无须得出最终的结论θ=0.7。事实上,根据贝叶斯法则,0.7是一个不太可能的取值(如果你知道几乎所有的硬币都是均质的,那么这个实验并没有提供足够的证据来说服你,它是均质的)。但是,0.7却是最大似然估计的取值。因为这里仅仅试验了一次,得到的样本太少,所以最终求出的最大似然值偏差较大,如果经过多次试验,扩充样本空间,则最终求得的最大似然估计将接近真实值0.5。在这篇博客中有详细的过程,就不再赘述。