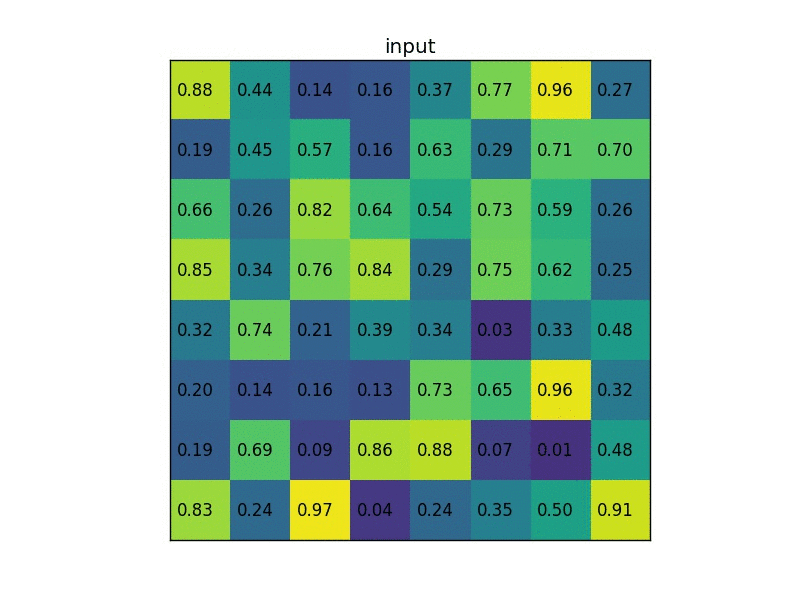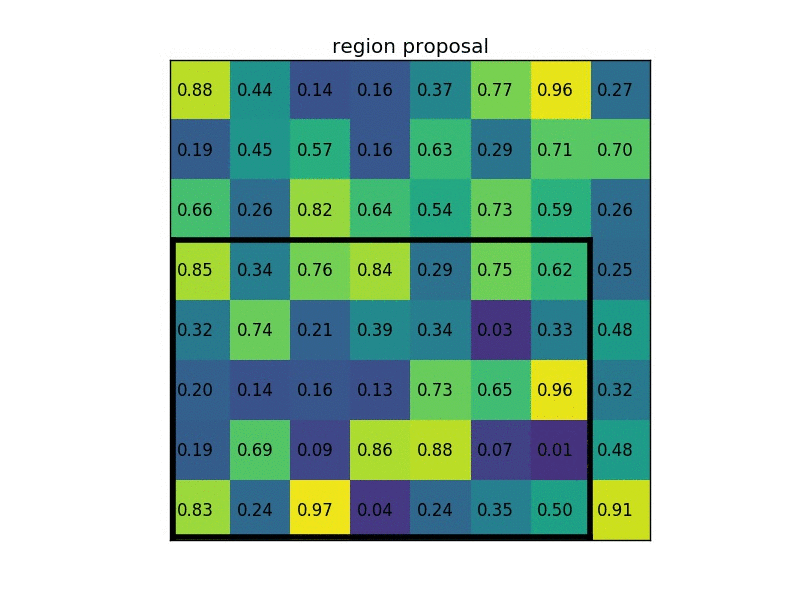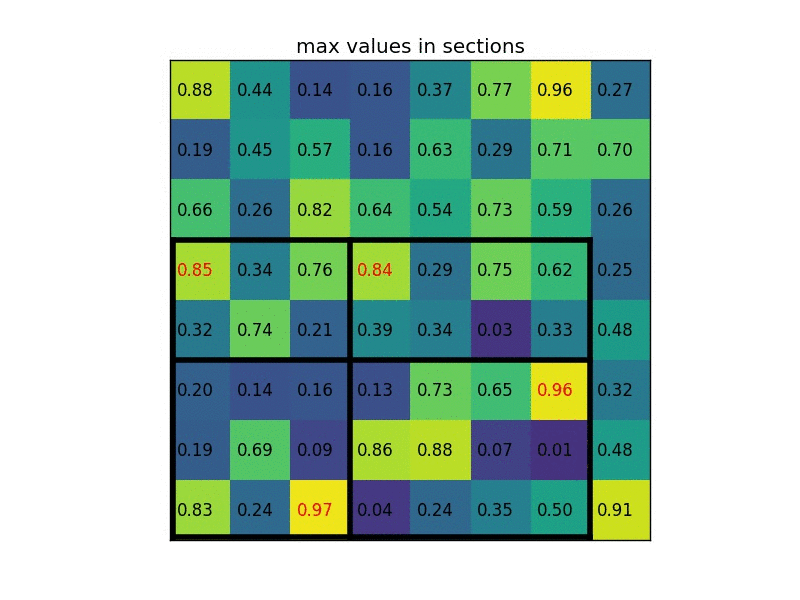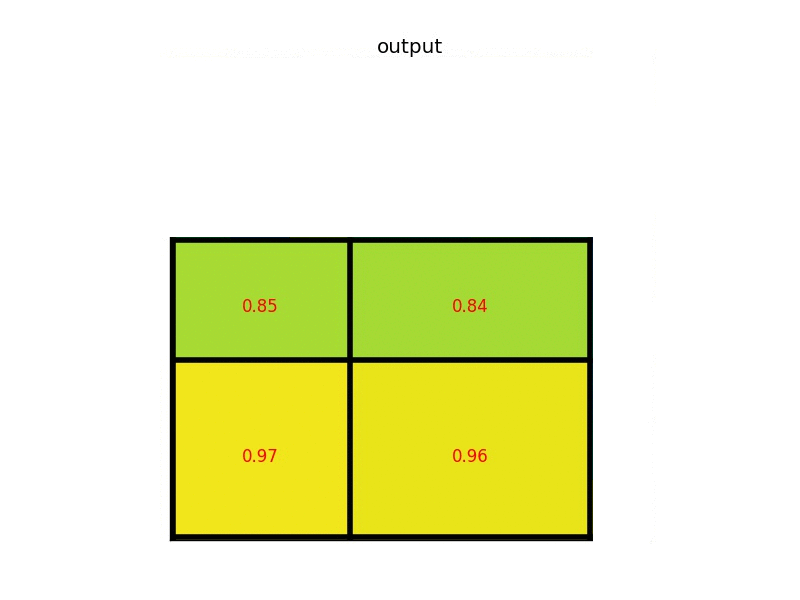
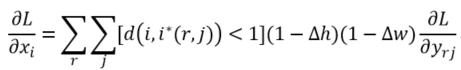ROI Align 是在Mask-RCNN这篇论文里提出的一种区域特征聚集方式, 很好地解决了ROI Pooling操作中两次量化造成的区域不匹配(mis-alignment)的问题。
其中ROI Align用的是双线性插值(内插)来实现的,在分析源码前我们先来了解下什么是双线性插值。
插值定义:函数 y=f(x)在区间[a, b]上(n+1)个互异点xi(i=0,1,2...n)上的函数值yi,若存在一简单函数g(x),使得g(xi)=yi并要求误差
R(x) = f(x) - g(x)的绝对值在整个区间[a, b]上比较小。这样的问题称为插值问题。
其中线性插值是一种较为简单的插值方法,其插值函数为一次多项式。线性插值,在各插值节点上插值的误差为0
假设函数y=f(x)在两点x0, x1上的值分别为y0, y1 求多项式 y=g(x)=b+kx 是满足 g(x0)=y0,g(x1)=y1
很显然g(x)就是过(x0, y0),(x1, y1)的直线 表达式y=g(x)=y0 + (y1-y0)/(x1-x0) * (x-x0) (别告诉这个推不出来~)
一般称f(xj)-f(xi)/xj-xi 为f(x)在xi,xj处的一阶均差,记为f(xi,xj)。于是g(x)=f(x0)+f(x1,x0)(x-x0)
如果按照y0,y1整理 g(x)=(x-x1)/(x0-x1) * y0 + (x-x0)/(x1-x0) * y1
简单来说 线性差值就是在某一区间内用直线L(x)来近似原函数f(x)(在一定误差允许下)
下面进入正题 什么是双线性插值以及公式怎么推导:

假如我们想得到未知函数f在点P= (x,y) 的值,假设我们已知函数f在Q11 = (x1,y1)、Q12 = (x1,y2),Q21 = (x2,y1) 以及Q22 = (x2,y2) 四个点的值。
首先在x方向进行线性插值,得到R1和R2,然后在y方向进行线性插值,得到P.
这样就得到所要的结果f(x,y).
第一步:X方向的线性插值,在Q12,Q22中插入蓝色点R2,Q11,Q21中插入蓝色点R1;
第二步 :Y方向的线性插值 ,通过第一步计算出的R1与R2在y方向上插值计算出P点。
线性插值的结果与插值的顺序无关。首先进行y方向的插值,然后进行x方向的插值,所得到的结果是一样的。双线性插值的结果与先进行哪个方向的插值无关。
如果选择一个坐标系统使得 的四个已知点坐标分别为 (0, 0)、(0, 1)、(1, 0) 和 (1, 1),那么插值公式就可以化简为
f(x,y)=f(0,0)(1-x)(1-y)+f(1,0)x(1-y)+f(0,1)(1-x)y+f(1,1)xy (嗯...一步到胃 没看懂?没关系下面我们来推导下)
我们记 Q12 坐标为(0, 0) Q22 坐标为(1, 0) Q11坐标为(0, 1) Q21(1, 1) P点坐标为(x, y) x,y 属于(0, 1)肯定有人问为什么坐标这样 我只能说我喜欢这样咋滴!(开个玩笑~)其实是因为我们图像坐标就是这么记得 左上角记为(0, 0) 右下角(1, 1)
按照第一步:X方向的线性插值 (0, 0) (1, 0)中插入R2 可以得到R2点表达式:
R2 = f(0, 0) + (f(1, 0) - f(0, 0))* x
(0, 1) (1, 1)中插入R1 可以得到R1点的表达式
R1 = f(0, 1) + (f(1, 1), - f(0, 1)) * x
按照第二步:Y方向的线性插值 ,通过第一步计算出的R1与R2在y方向上插值计算出P点
P点表达式 f(x, y) = f(x, 0) + (f(x, 1) - f(x, 0)) * y 其中 f(x, 0)就是点R2 f(x, 1)就是点R1 带入表达式
P = f(x, y) = R2 + (R1 - R2) * y = f(0, 0) + (f(1, 0) - f(0, 0))* x + (f(0, 1) + (f(1, 1), - f(0, 1)) * x - f(0, 0) - (f(1, 0) - f(0, 0))* x)*y
= (1 - x - y + xy) * f(0, 0) + (x - xy) * f(1, 0) + (y - xy) * f(0, 1) + xy * f(1, 1)
= f(0,0)(1-x)(1-y)+f(1,0)x(1-y)+f(0,1)(1-x)y+f(1,1)xy
好了 数学问题到此结束 还没看懂的 请双脚离地!!!
下面开始正文源码解读 源码地址https://github.com/AceCoooool/RoIAlign-RoIPool-pytorch github上随便找的一个其实实现都是一样的懂了原理就行
ROI Align 的forward
/* -----------------------------begin for forward--------------------------------- */
template<typename T>
void pre_calc_for_bilinear(const int h, const int w, const int pool_h, const int pool_w, int b_grid_h, int b_grid_w,T start_y, T start_x, T b_size_h, T b_size_w, vector<PreCalc<T>> &pre_calc) {int idx = 0;// 开始遍历每个binfor (int ph = 0; ph < pool_h; ++ph) {for (int pw = 0; pw < pool_w; ++pw) {for (int iy = 0; iy < b_grid_h; ++iy) {// 为没个bin采样四个点 其位置相对于每个bin的坐标位置为 (0.25, 0.25) (0.25, 0.75) (0.75, 0.25) (0.75, 0.75)const T yy = start_y + ph * b_size_h + static_cast<T>(iy + 0.5f) * b_size_h / static_cast<T>(b_grid_h);for (int ix = 0; ix < b_grid_w; ++ix) {const T xx =start_x + pw * b_size_w + static_cast<T>(ix + 0.5f) * b_size_w / static_cast<T>(b_grid_w);T x = xx, y = yy;// situation 1: out of rangeif (y < -1.0 || y > h || x < -1.0 || x > w) {PreCalc<T> pc{0, 0, 0, 0, 0, 0, 0, 0};pre_calc[idx] = pc;idx += 1;continue;}// not exceed 1.0y = y <= 0 ? 0 : (y >= h - 1 ? h - 1 : y);x = x <= 0 ? 0 : (x >= w - 1 ? w - 1 : x);// x y 向下取整int y_low = (int) y;int x_low = (int) x;int y_high = y_low >= h - 1 ? y_low : y_low + 1;int x_high = x_low >= w - 1 ? x_low : x_low + 1;// 这里就是双线性插值公式了 low 就是 f(0, 0) high 就是 f(1, 1)// f(x,y)=f(0,0)(1-x)(1-y)+f(1,0)x(1-y)+f(0,1)(1-x)y+f(1,1)xyT ly = y - y_low, lx = x - x_low;T hy = 1.0 - ly, hx = 1.0 - lx;T w1 = hy * hx, w2 = hy * lx, w3 = ly * hx, w4 = ly * lx;// in the feature map's position and correspond weightsPreCalc<T> pc;// 这四个点就是对应的 f(0, 0) f(1, 0) f(0,1) f(1, 1)// 应为这里是返回该点所在feature_map上的索引位置 不是坐标位置所以进行转换 y * width + x// 至于为什么是y * width + x 就和feature_map的数据存储有关了 因为feature_map存储格式是一维数组// 长度为 n * c * h * w 这里我们只需要考虑具体的某一张特征图 h * w // 对应矩阵 (h, w )中每一点转到一维数组的坐标就是 y * width + x// 有人要问 n, c? 哪里去了 这很简单因为这里不需要计算 因为对应一个roi来说 在对应feature_map每个通道上的位置都是一样的// 所以这里是把双线性插值的计算方法抽取出来公用 pc.pos1 = y_low * w + x_low;pc.pos2 = y_low * w + x_high;pc.pos3 = y_high * w + x_low;pc.pos4 = y_high * w + x_high;pc.w1 = w1, pc.w2 = w2, pc.w3 = w3, pc.w4 = w4;pre_calc[idx] = pc;idx += 1;} // b_grid_w} // b_grid_h} // pool_w} // pool_h
}template<typename T>
void roi_align_forward(const T *feat, const T *rois, const vector<int64_t> &feat_size,const vector<int64_t> &rois_size, const T &scale, const int ratio, T *out) {const int n_rois = rois_size[0], col_rois = rois_size[1], pool_h = rois_size[2], pool_w = rois_size[3];const int channel = feat_size[1], h = feat_size[2], w = feat_size[3];/**** n_rois 表示的是有多少个roi (region of interest)* col_rois 表示的是一个rois是几列组成的 如果是4列就是(x1, y1, x2, y2) 如果是5列(batch_id, x1, y1, x2, y2)* pool_h pool_w 池化后的高宽* channel 通道数 * h, w feature_maps的尺寸 也就是特征图的大小* 这里我们主要注意下输出的格式* T * out 可以理解为一个数组 数组长度 n * c * pool_h * pool_w* 可以理解为 (n, c, h, w)的矩阵reshape成(-1, 1) 这种存储数据格式是计算方便 因为我们会将这个大数组用连续内存存储* 因为我们会频繁的操作这些数据 所以用连续的内存块存储存取都更方便这样每一只需要指针移动一步就是读取下一个数据,* 这种存储结构在正向反向传播是更方便* * 同理对于feature_maps也就是特征图也是上面的存储格式也存在 一个 n * c * h * w 的数组中***/// #pragma omp parallel forfor (int n = 0; n < n_rois; ++n) {// 知道了数据的存储格式也就是说 对于每一个roi我们需要分配 c * pool_h * pool_w 长度的数组// n * channel * pool_h * pool_w 表示数组的开始位置索引int idx_n = n * channel * pool_h * pool_w;// rois data// 这里的 rois是一个指针只想了存储rois数组的指针 也是上面类似的存储格式 存储在 col_rois * n_rois长度的数组中 // 每col_rois列表示一个roi的位置信息// 下面的代码表示指针在数组上移动col_rois个位置const T *offset_rois = rois + col_rois * n;int roi_batch_idx = 0;if (col_rois == 5) {// 如果col_rois为5 第一个为batch_id roi_batch_idx = offset_rois[0];// offset_rois移动到下一个位置 跳过第一个位置batch_id++offset_rois;}// Do not using rounding; this implementation detail is critical// 这里是将roi坐标(x1, y1, x2, y2)映射到特征图上T start_x = offset_rois[0] * scale;T start_y = offset_rois[1] * scale;T end_x = offset_rois[2] * scale;T end_y = offset_rois[3] * scale;// Force malformed ROIs to be 1x1// 计算roi映射到特征图后的的宽高T roi_w = std::max(end_x - start_x, (T) 1.);T roi_h = std::max(end_y - start_y, (T) 1.);// 这表示每个bin的大小 将特征图分成pool_w * pool_h个区间 每个区间就是一个binT bin_size_w = roi_w / static_cast<T>(pool_w);T bin_size_h = roi_h / static_cast<T>(pool_h);// We use roi_bin_grid to sample the grid and mimic integral// 这个表示每个bin的采样个数 论文中是采样四个点(w 上两个 h上两个) 然后最大池化 这里是取得平均池化// 如果没有设置采样个数就用 roi_h / pool_hint bin_grid_h = (ratio > 0) ? ratio : std::ceil(roi_h / pool_h);int bin_grid_w = (ratio > 0) ? ratio : std::ceil(roi_w / pool_w);// We do average (integral) pooling inside a bin// 这里其实就是 4const T count = bin_grid_h * bin_grid_w;// get each bin's corresponding position and weights// 计算双线性差值 这里只计算每个bin的 四个采样点位置和权重 // 这里返回的是一个vector vector长度为 pool_h * pool_w * 4 // 总共有 pool_h * pool_w 个bin 每个bin采样四个点 每个点都采用双线性插值计算该采样点值// vector中的数据格式 PreCalc<T> pc; 这里面存了 四个点在feature_map中的位置信息 和四个点的权重// 利用双线性插值公式可以计算出采样点的真的数组std::vector<PreCalc<T>> pre_calc(count * pool_h * pool_w);pre_calc_for_bilinear(h, w, pool_h, pool_w, bin_grid_h, bin_grid_w, start_y, start_x, bin_size_h, bin_size_w,pre_calc);// map to feature mapfor (int c = 0; c < channel; ++c) {// 遍历通道 idx_nc 表示第 n个 roi 第c个通道所在数组起始位置int idx_nc = idx_n + c * pool_w * pool_h;const T *offset_feat = feat + (roi_batch_idx * channel + c) * h * w;// pre_calc_idx用来计数遍历到哪个bin了int pre_calc_idx = 0;// 遍历 pool_h pool_w 也就是遍历每个binfor (int ph = 0; ph < pool_h; ++ph) {for (int pw = 0; pw < pool_w; ++pw) {// 每个bin在返回out数组中的索引位置int idx = idx_nc + ph * pool_w + pw;T output_val = 0.;// 这里是将四个采样点相加 除以count 也就是平均池化for (int iy = 0; iy < bin_grid_h; ++iy) {for (int ix = 0; ix < bin_grid_w; ++ix) {// 取出该bin对应的双线性插值位置和权重计算输出值PreCalc<T> pc = pre_calc[pre_calc_idx];output_val += pc.w1 * offset_feat[pc.pos1] + pc.w2 * offset_feat[pc.pos2] +pc.w3 * offset_feat[pc.pos3] + pc.w4 * offset_feat[pc.pos4];pre_calc_idx += 1;}}// 这里就是直接赋值output_val /= count;out[idx] = output_val;} // for pw} // for ph} // for c} // for rois_n
}到这里我相信大家已经完全理解了roi align是怎么forward的 话不多说直接看 backward
ROI Align 的backward
template<class T>
inline void add(const T &val, T *address) {// 这个函数就很简单了 就是累加值 *address += val;
}template<typename T>
void bilinear_interpolate_gradient(const int h, const int w, T y, T x, PreCalc<T> &pc) {if (y < -1.0 || y > h || x < -1.0 || x > w) {pc = {-1, -1, -1, -1, 0., 0., 0., 0.};return;}// 计算该样本点对应的4个用于双线性插值的点的位置和权重// not exceed 1.0y = y <= 0 ? 0 : (y >= h - 1 ? h - 1 : y);x = x <= 0 ? 0 : (x >= w - 1 ? w - 1 : x);int y_low = (int) y;int x_low = (int) x;int y_high = y_low >= h - 1 ? y_low : y_low + 1;int x_high = x_low >= w - 1 ? x_low : x_low + 1;// 得到四个点在feature_map上的位置和计算的权重pc.pos1 = y_low * w + x_low;pc.pos2 = y_low * w + x_high;pc.pos3 = y_high * w + x_low;pc.pos4 = y_high * w + x_high;T ly = y - y_low, lx = x - x_low;T hy = 1.0 - ly, hx = 1.0 - lx;pc.w1 = hy * hx, pc.w2 = hy * lx, pc.w3 = ly * hx, pc.w4 = ly * lx;
}template<typename T>
void roi_align_backward(int total, const T *rois, T *grad_out, const T &scale, const vector<int64_t> feat_size,const int pool_h, const int pool_w, const int rois_col, const int sample, T *grad_in) {// total=nxcxphxpwauto channel = feat_size[0], h = feat_size[1], w = feat_size[2];// 从idx 反推 n c pool_h pool_w // 我们可以从forward看出 output是个数组 长度为 n * c * h * wfor (int idx = 0; idx < total; ++idx) {int pw = idx % pool_w;int ph = (idx / pool_w) % pool_h;int c = (idx / pool_h / pool_w) % channel;int n = idx / pool_h / pool_w / channel;// 这里和forward是一致的const T *offset_rois = rois + n * rois_col;int roi_batch_idx = 0;if (rois_col == 5) {roi_batch_idx = offset_rois[0];++offset_rois;}// Do not using rounding; this implementation detail is critical// 这里和forward是一致的 将roi的坐标映射到feature_map特征图上T start_x = offset_rois[0] * scale;T start_y = offset_rois[1] * scale;T end_x = offset_rois[2] * scale;T end_y = offset_rois[3] * scale;// Force malformed ROIs to be 1x1// 这里和forward是一致的T roi_w = std::max(end_x - start_x, (T) 1.0);T roi_h = std::max(end_y - start_y, (T) 1.0);T b_size_h = roi_h / static_cast<T>(pool_h);T b_size_w = roi_w / static_cast<T>(pool_w);// 注意这里 grad_in是指针数组存储了输入梯度 长度为 n * c * h * w 对应feature_map中各值的梯度// offset_grad_in 指向了当前的特征图第n张图片 第c个通道的featuer_map的梯度起始位置T *offset_grad_in = grad_in + (roi_batch_idx * channel + c) * h * w;// 注意这里 grad_out是指针数组存储了输出梯度 长度为 n * c * pool_h * pool_w 对应roialign后feature_map中各值的梯度// offset_grad_in 指向了当前的特征图第n张图片 第c个通道的roialign后ffeatuer_map的梯度起始位置T *offset_grad_out = grad_out + (n * channel + c) * pool_h * pool_w;// grad_out_this_bin 表示指向了在roialign后梯度特征图上的具体位置T grad_out_this_bin = offset_grad_out[ph * pool_w + pw];// We use roi_bin_grid to sample the grid and mimic integralint roi_bin_grid_h = (sample > 0) ? sample : std::ceil(roi_h / pool_h);int roi_bin_grid_w = (sample > 0) ? sample : std::ceil(roi_w / pool_w);// We do average (integral) pooling inside a binconst int count = roi_bin_grid_h * roi_bin_grid_w;PreCalc<T> pc;// 计算梯度反传 遍历grad_out_this_bin指向的位置的四个采样点for (int iy = 0; iy < roi_bin_grid_h; iy++) {const T y = start_y + ph * b_size_h +static_cast<T>(iy + .5f) * b_size_h / static_cast<T>(roi_bin_grid_h); // e.g., 0.5, 1.5for (int ix = 0; ix < roi_bin_grid_w; ix++) {const T x = start_x + pw * b_size_w +static_cast<T>(ix + .5f) * b_size_w / static_cast<T>(roi_bin_grid_w);// 得到用于计算每个采样点的值得 4个用于双线性差值的四个点的位置和权重信息bilinear_interpolate_gradient(h, w, y, x, pc);// 将梯度反传到拥有计算双线性差值的四个点T g1 = grad_out_this_bin * pc.w1 / count;T g2 = grad_out_this_bin * pc.w2 / count;T g3 = grad_out_this_bin * pc.w3 / count;T g4 = grad_out_this_bin * pc.w4 / count;// update grad_outif (pc.pos1 >= 0 && pc.pos2 >= 0 && pc.pos3 >= 0 && pc.pos4 >= 0) {// 将梯度累加到对应输入位置 因为该点可能参与了多次计算所以是需要累加的// 所有用到过该点的梯度度需要反传add(g1, offset_grad_in + pc.pos1);add(g2, offset_grad_in + pc.pos2);add(g3, offset_grad_in + pc.pos3);add(g4, offset_grad_in + pc.pos4);}} // for ix} // for iy} // for
}本来到此应该结束了,但我估计有人会有疑问 下面这几个式子啥意思啊?你说他是梯度他就是梯度了啊!别闹~
// 将梯度反传到拥有计算双线性差值的四个点
T g1 = grad_out_this_bin * pc.w1 / count;
T g2 = grad_out_this_bin * pc.w2 / count;
T g3 = grad_out_this_bin * pc.w3 / count;
T g4 = grad_out_this_bin * pc.w4 / count;
既然这样我们来推导下这几个公式怎么来的
首先对于一个bin区间内有四个采样点每个采样点 的计算公式是
xi = w1 * f(pos1) + w2 * f(pos2) + w3 * f(pos3) + w4 * f(pos4)
xi 表示第i个采样点的值 f(pos1) 表示feature_map位于pos1的值 i = 1, 2, 3, 4
我们的输出y = (x1 + x2 + x3 + x4) /4
已知dy 求 df(pos1) df(pos2) df(pos3) df(pos4)
根据链式法则 df(pos1) = dy * △y/△xi * △xi/ f(pos1) = dy * 1/4 * w1
对应T g1 = grad_out_this_bin * pc.w1 / count;
然后将pos1位置的梯度累加回grad_in
我想最后还会有人说 你这最后是平均池化 不是最大池化 论文中使用的是最大池化!!!
对于这个我只想说 还要不要人活了?~
对于这个我简单实现下 其实也很简单 懂了上面的平均池化 最大池化有难度嘛?肯定没有塞!!!
最大池化-forward
只需要在上面for循环中 取四个采样点的最大值
然后用一个 argmax_data数据记录最大值所在的索引位置信息
for (int c = 0; c < channel; ++c) {int idx_nc = idx_n + c * pool_w * pool_h;const T *offset_feat = feat + (roi_batch_idx * channel + c) * h * w;int pre_calc_idx = 0;for (int ph = 0; ph < pool_h; ++ph) {for (int pw = 0; pw < pool_w; ++pw) {int idx = idx_nc + ph * pool_w + pw;T output_val = 0.;int index = 0for (int iy = 0; iy < bin_grid_h; ++iy) {for (int ix = 0; ix < bin_grid_w; ++ix) {PreCalc<T> pc = pre_calc[pre_calc_idx];// output_val += pc.w1 * offset_feat[pc.pos1] + pc.w2 * offset_feat[pc.pos2] +// pc.w3 * offset_feat[pc.pos3] + pc.w4 * offset_feat[pc.pos4];// 去掉累加 求和直接用最大值代替 if offset_feat[pc.pos1] > output_val:output_val = offset_feat[pc.pos1]index = pc.pos1if offset_feat[pc.pos2] > output_val:output_val = offset_feat[pc.pos2]index = pc.pos2if offset_feat[pc.pos3] > output_val:output_val = offset_feat[pc.pos3]index = pc.pos3if offset_feat[pc.pos4] > output_val:output_val = offset_feat[pc.pos4]index = pc.pos4pre_calc_idx += 1;}}
// output_val /= count;out[idx] = output_val;// 添加一个标记最大值位置的索引 argmax_data[idx] = index} // for pw} // for ph} 最大池化-backward
offset_argmax_data 就是上面forward存储的 argmax_data最大池化的梯度只会回传给四个采样点中最大值位置 其余采样点不会回传梯度 而且计算方式稍微有些变化
// 计算梯度反传 遍历grad_out_this_bin指向的位置的四个采样点for (int iy = 0; iy < roi_bin_grid_h; iy++) {const T y = start_y + ph * b_size_h +static_cast<T>(iy + .5f) * b_size_h / static_cast<T>(roi_bin_grid_h); // e.g., 0.5, 1.5for (int ix = 0; ix < roi_bin_grid_w; ix++) {const T x = start_x + pw * b_size_w +static_cast<T>(ix + .5f) * b_size_w / static_cast<T>(roi_bin_grid_w);// 得到用于计算每个采样点的值得 4个用于双线性差值的四个点的位置和权重信息bilinear_interpolate_gradient(h, w, y, x, pc);// 将梯度反传到拥有计算双线性差值的四个点T g1 = grad_out_this_bin * pc.w1;T g2 = grad_out_this_bin * pc.w2;T g3 = grad_out_this_bin * pc.w3;T g4 = grad_out_this_bin * pc.w4;
// T g1 = grad_out_this_bin * pc.w1 / count;
// T g2 = grad_out_this_bin * pc.w2 / count;
// T g3 = grad_out_this_bin * pc.w3 / count;
// T g4 = grad_out_this_bin * pc.w4 / count;// update grad_outif (pc.pos1 >= 0 && pc.pos2 >= 0 && pc.pos3 >= 0 && pc.pos4 >= 0) {// 将梯度累加到对应输入位置 因为该点可能参与了多次计算所以是需要累加的// 所有用到过该点的梯度度需要反传if(offset_argmax_data[ph * pool_width + pool_h] == pc.pos1){add(g1, offset_grad_in + pc.pos1);}if(offset_argmax_data[ph * pool_width + pool_h] == pc.pos2){add(g2, offset_grad_in + pc.pos2);}if(offset_argmax_data[ph * pool_width + pool_h] == pc.pos3){add(g3, offset_grad_in + pc.pos3);}if(offset_argmax_data[ph * pool_width + pool_h] == pc.pos4){add(g4, offset_grad_in + pc.pos4);}
// add(g1, offset_grad_in + pc.pos1);
// add(g2, offset_grad_in + pc.pos2);
// add(g3, offset_grad_in + pc.pos3);
// add(g4, offset_grad_in + pc.pos4);}} // for ix} 以上都是个人理解并手码的 可能会有理解错误和手误,如果有错误欢迎指正!!! (反正我不改~)
以上均为原创,转载请添加来源谢谢!!!