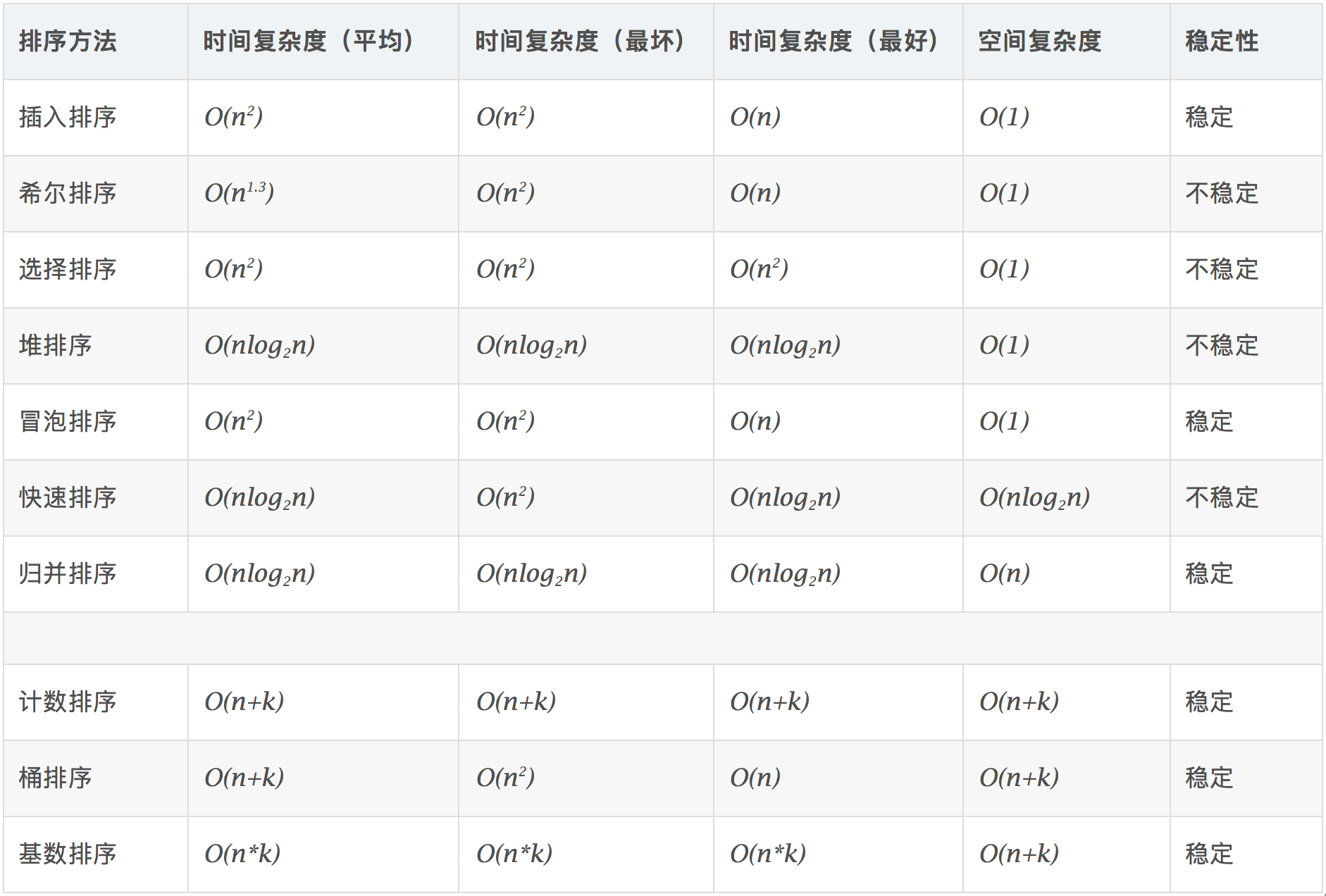
文章目录

一、冒泡排序

思想：

从第一个数开始依次向后进行比较（第一个和第二个比较然后第二个和第三个比较……）若前一个数大于后一个数交换两数位置。一直比较到最后第N-1个数和第N个数比较。目的是将这组数中最大的数放到最后，然后对剩下的N-1个数进行相同操作将剩余N-1个数中最大的数放到倒数第二个位置。重复这一操作N-1次。

动图演示：

 代码实现：

void Bubble_Sort(int* arr, int len)//len为数组长度
{for (int i = 1; i < len; i++)//规定总的比较轮数{bool tar = true;//标记一轮比较是否有交换for (int j = 0; j < len - i; j++)//每一轮比较{if (arr[j] > arr[j + 1])//判断前一个数是否大于后一个数若大于交换{int tmp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = tmp;tar = false;}}if (tar)//若一轮比较无交换结束break;}
}

注：该代码为小优化后的代码（加了一个记录标记） 

算法分析：

 时间复杂度：O（n^2）

空间复杂度：O（1）

稳定性：稳定

二、选择排序

思想：

从第一个数据开始找出从这个数开始到最后一个数中最小的数将其与开始的那个数交换，然后从第二个数开始重复上述操作一直到倒数第二个数为止。

动图演示：

 代码实现：

void Choose_Sort(int* arr, int len)//len为数组长度
{int tmp;//交换时的中间变量for (int i = 0; i < len - 1; i++)//规定交换轮数{int min = i;//记录每轮最小值下标for (int j = i + 1; j < len; j++)//每轮对比{if (arr[j] < arr[min])min = j;}//每轮结束后的交换（将最小值交换到开头）tmp = arr[i];arr[i] = arr[min];arr[min] = tmp;}
}

算法分析：

时间复杂度：O（n^2）

空间复杂度：O（1）

稳定性：不稳定 

三、直接插入排序

思想：

从第二个数开始向前寻找第一个不大于它自身的数插入到其后面，然后从第三个数开始向前寻找……直到最后一个数为止。

动图演示：

代码实现：

void Insert_Sort(int* arr, int len)//len为数组长度
{int j;for (int i = 1; i < len ; i++)//规定交换轮数{int tmp = arr[i];//记录每轮要对比的数for (j = i-1; j >=0; j--)//每轮对比{if (arr[j] > tmp)//如果该数大于对比数该数向后挪动一位arr[j + 1] = arr[j];else//找到第一个比它小的数结束break;}//每轮结束后将对照数插入到目标位置arr[j+1] = tmp;}
}

 算法分析：

时间复杂度：O （n^2）

空间复杂度：O（n^2）

稳定性：稳定

四、希尔排序

思想：

对比较有序的数据进行排序，即先将每隔素数个数据划分为一组进行排序（进行多次素数划分（每次素数不同）并排序）使其较为有序最后在较为有序的基础上再对其进行一个一个进行排序。（是简单插入排序的优化）

动图演示：

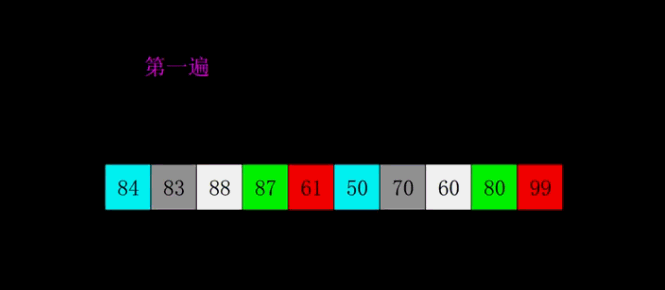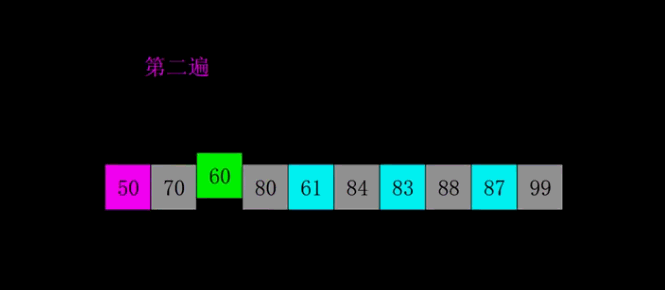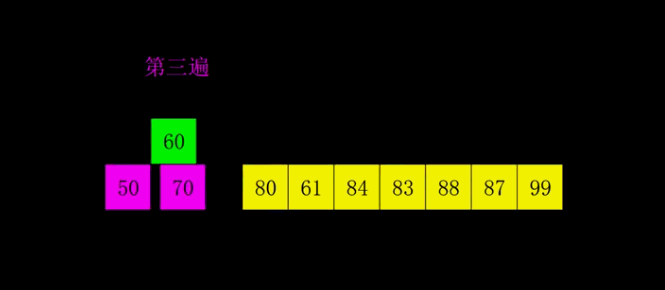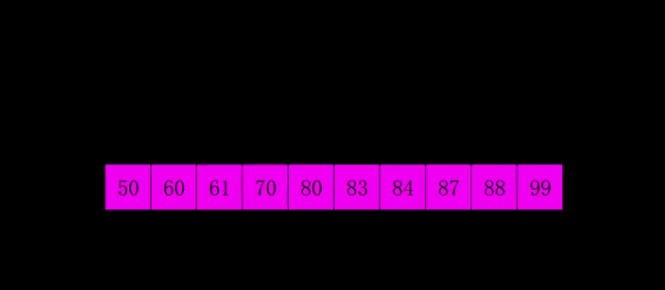
 代码实现：

void Shell(int* arr, int len, int gap)//单次排序函数，gap为划分的素数间隔
{int j;for (int i = gap; i < len; i++)//总排序轮数{int tmp = arr[i];//每一轮对比数for (j = i - gap; j >= 0; j -= gap)//单轮对比{if (arr[j] > tmp){arr[j + gap] = arr[j];}elsebreak;}arr[j + gap] = tmp;}
}
void Shell_Sort(int* arr, int len)//len为数组长度
{int brr[3] = { 1,3,5 };//要划分数据的素数for (int i = 2; i >= 0; i--)//进行相应划分后数据的排序{Shell(arr, len, brr[i]);}
}

注：该代码为分别用【5，3，1】间隔进行排序的代码。 

算法分析：

时间复杂度：O（n^1.3）~ O（n^2）

空间复杂度：O  ( 1 ) 

稳定性：不稳定 

五、归并排序

思想：

首先将数据一个一个分为N个数组然后俩俩合并相邻数组。重复合并数组操作到最后只剩下一个数组。

图像分析：

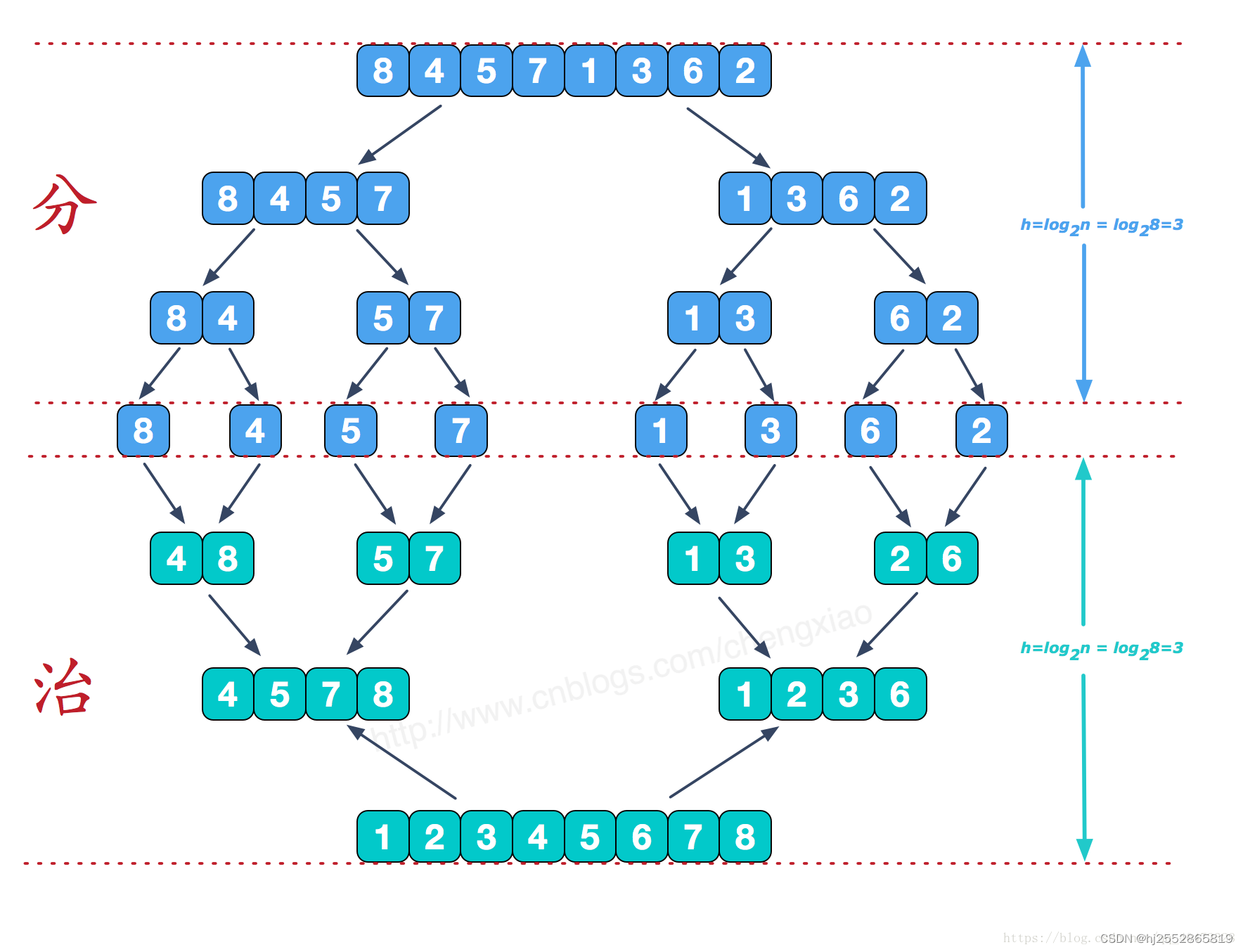
 代码实现：

void Merge(int* arr, int len, int gap)//单次数组合并，len为数组长度，gap为划分的数组中元素数量
{int* brr = (int*)malloc(len * sizeof(int));//开辟一个等长数组用来承载数组俩俩合并后的数据int k = 0;int low1 = 0;//合并的俩个数组中第一个数组当前下标int high1 = low1 + gap - 1;//合并的俩个数组中第一个数组末尾下标int low2 = high1 + 1;合并的俩个数组中第二个数组当前下标int high2 = (low2 + gap - 1)>(len-1)?len-1:low2+gap-1;//合并的俩个数组中第二个数组末尾下标while (low2 < len)//当第二个数组不存在时结束{while (low1 <= high1 && low2 <= high2)//当二个数组都有数据时比较{if (arr[low1] > arr[low2])brr[k++] = arr[low2++];elsebrr[k++] = arr[low1++];}while (low1 <= high1)//当第一个数组还有数据时将其全部写入brr中{brr[k++] = arr[low1++];}while (low2 <= high2)//当第二个数组还有数据时将其全部写入brr中{brr[k++] = arr[low2++];}//转到后面的二组数据low1 = high2 + 1;high1 = low1 + gap - 1;low2 = high1 + 1;high2 = (low2 + gap - 1) > (len - 1) ? len - 1 : low2 + gap - 1;}while (low1 < len)//如果还剩下一组数据将其写入brr中{brr[k ++] = arr[low1++];}for (int i = 0; i < len; i++)//将brr数据写入原数组中{arr[i] = brr[i];}
}
void Merge_Sort(int* arr, int len)
{for (int i = 1; i < len; i *= 2)//俩俩合并数组{Merge(arr, len, i);}
}

算法分析： 

时间复杂度：O（n*logn）

空间复杂度：O（n）

稳定性：稳定 

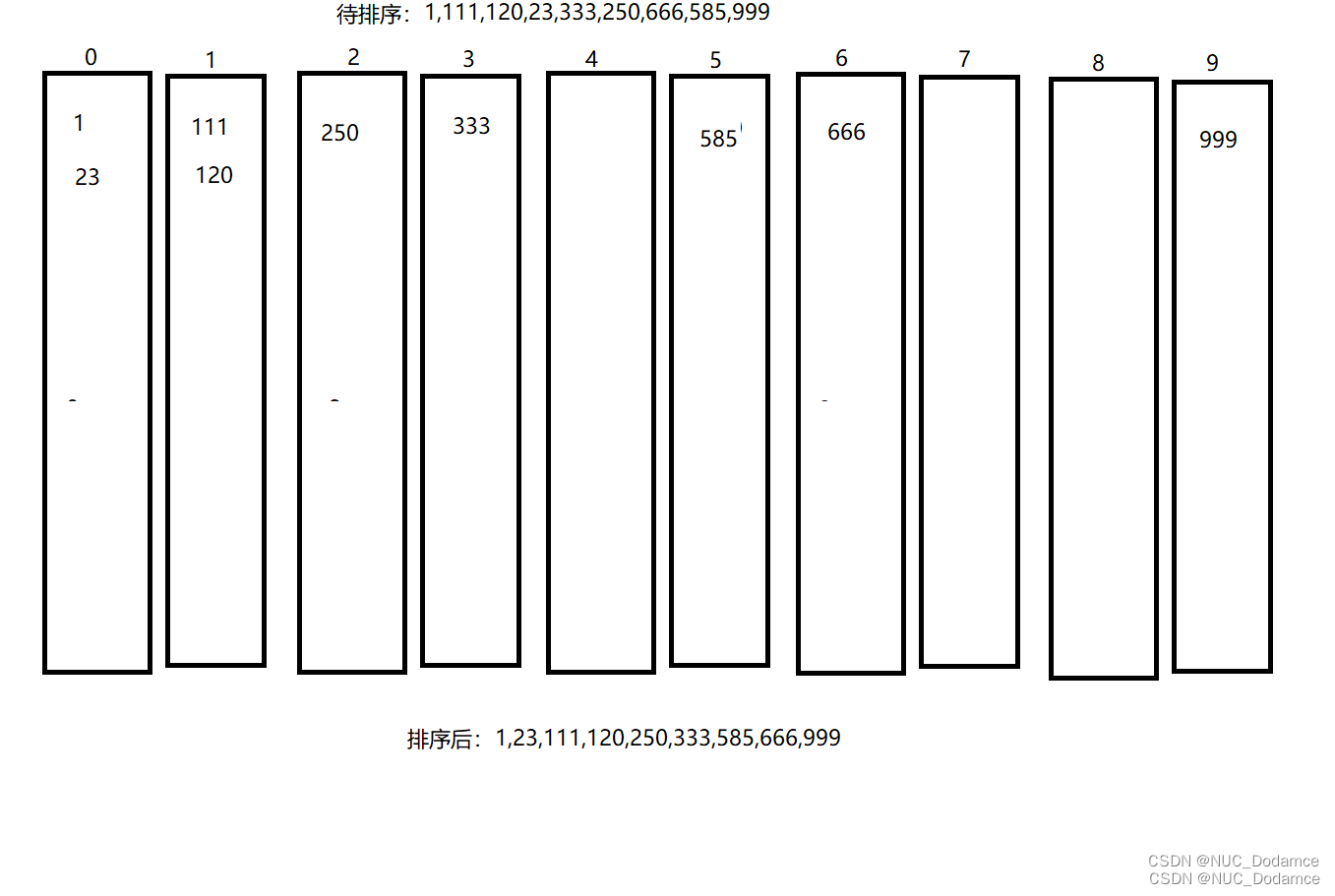
 六、基数（桶）排序

思想：

（假设这组数据中最大数位数为n）将这组数据分别按个位、十位、百位一直到n位排序。

动画演示：

代码实现：

int Get_Max_Num(int* arr, int len)//获取最大值位数
{int max = arr[0];//最大值int num=0;//位数for (int i = 1; i < len; i++)//寻找最大值{if (arr[i] > max)max = arr[i];}while (max != 0)//获取最大值位数{max = max / 10;num++;}return num;
}
void Radix(int* arr, int len, int num)//单次排序，num为该次排列的位数
{int n = pow(10, num-1);//当前位数int** brr=(int**)malloc(10 * sizeof(int*));//动态开辟二维空间记录排列后的结果（较为繁琐用链队列更好）for (int i = 0; i < 10; i++){brr[i] = (int*)malloc(len * sizeof(int));}int Brr[10] = { 0 };//计数器for (int i = 0; i < len; i++)//排列数据{int tmp = arr[i] / n % 10;brr[tmp][Brr[tmp]++] = arr[i];}int k = 0;for (int i = 0; i < 10; i++)//将排列好的数据重新写入数组{for (int j = 0; j < Brr[i]; j++){arr[k++] = brr[i][j];}free(brr[i]);}free(brr);
}
void Radix_Sort(int* arr, int len)
{int num=Get_Max_Num(arr, len);//获取最大值位数for (int i = 1; i <= num; i++)//进行排列{Radix(arr, len, i);}
}

注：该代码片段所展示的为“二维数组加计数”方法构建的基数算法但“链队列方法”构建更简单（C语言中链队列代码过长不方便展示）且该代码只考虑了数据为非负数情况（考虑负数情况代码较长不方便展示）。

算法分析：

时间复杂度：不太好确定（令最大数位数为m时间复杂度为O（m*n））

空间复杂度：O（n）

稳定性：稳定

七、堆排序

 思想：

堆排序借用大（小）顶堆根节点最大（最小）的思想通过一次次构建大（小）顶堆找出最大（最小）值然后将其与所构建大（小）顶堆的最后一个元素互换然后将最后一个元素排除在下一次构建之外重新构建大（小）顶堆循环往复直到所构建大顶堆仅有一个元素为止。

动图演示：

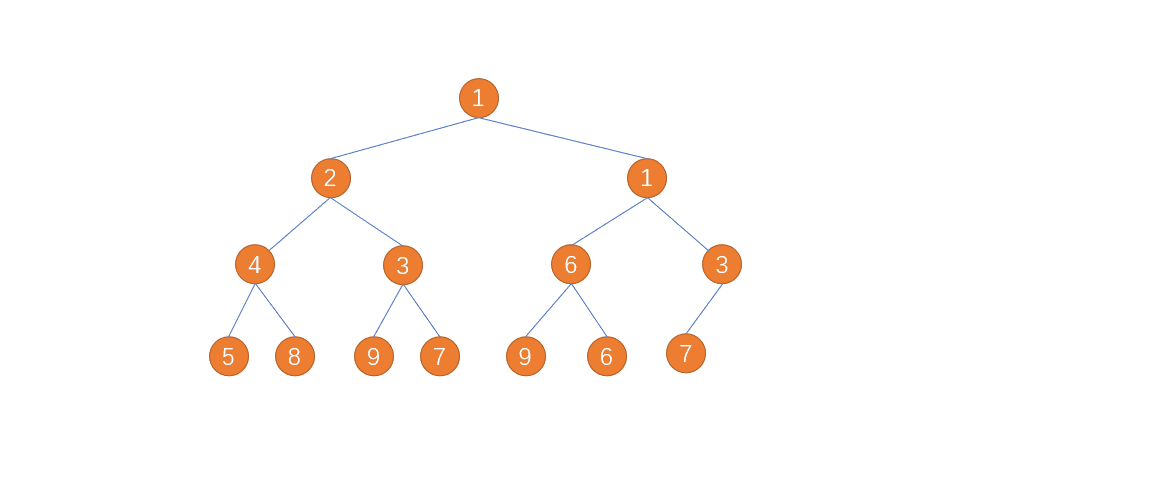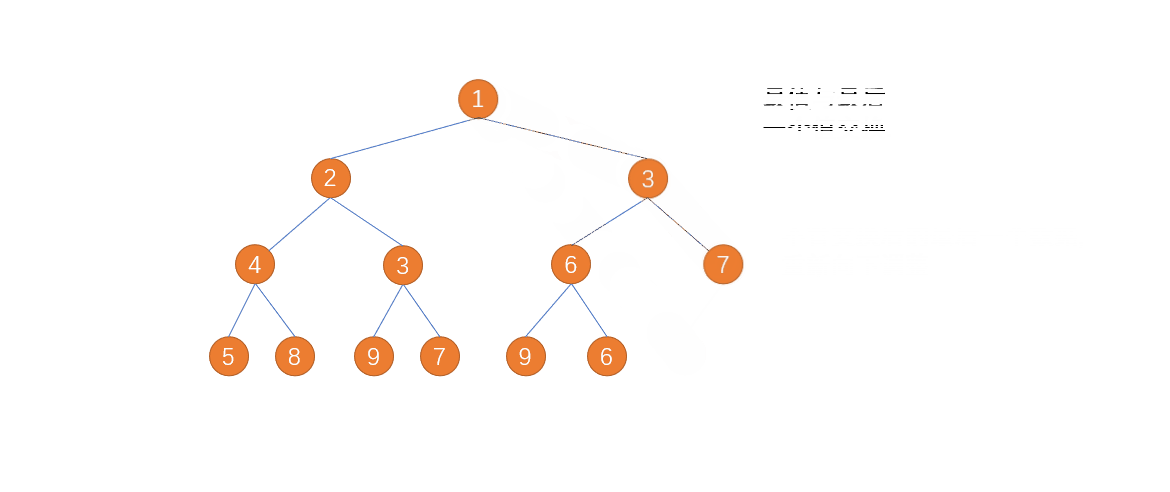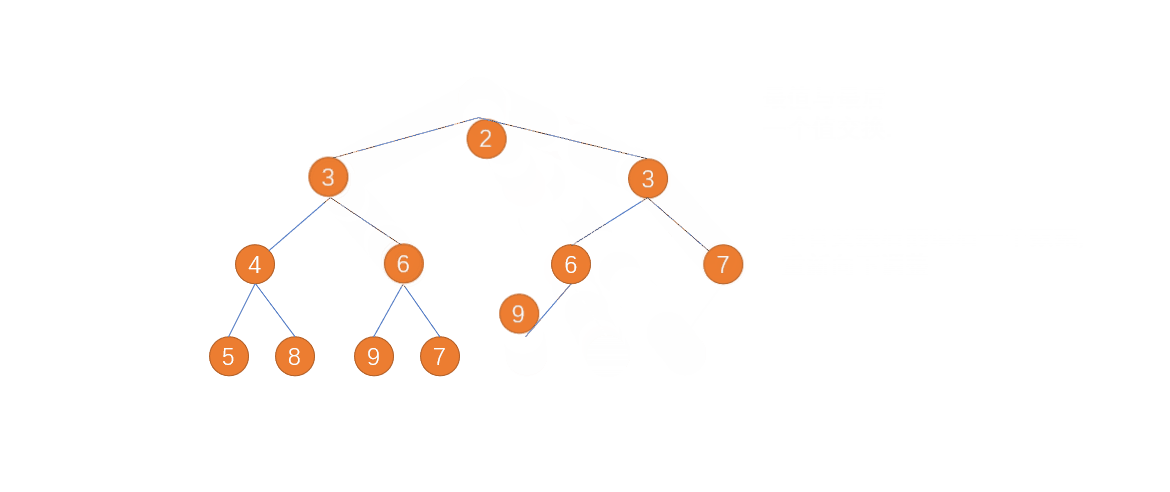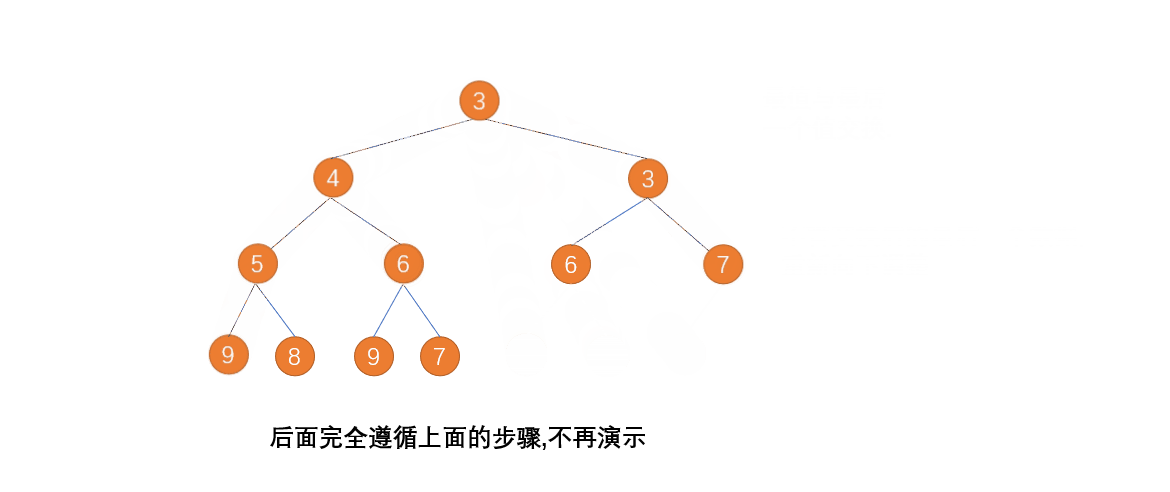
代码实现： 

void Heap_Adjust(int* arr,int start,int end)//单次构建大顶堆函数，start为本次构建大顶堆的根节点，end为本次构建的最后一个叶子
{int tmp=arr[start];//将未排序的根节点赋给tmp以方便下面的构建交换for (int i = start * 2; i <= end; i = i * 2)//构建大顶堆{if (i+1<=end && arr[i] < arr[i + 1])//若寻找到最大的次级分节点i++;if (arr[i] > tmp)//若寻找到最大的次级分节点大于当前节点进行交换{arr[start] = arr[i];start = i;//节点给下移}elsebreak;}arr[start] = tmp;//将根节点放入合适的位置
}
void Heap_Sort(int* arr, int len)
{for (int i = (len - 1) / 2; i >= 0; i--)//像构建一个整体大顶堆{Heap_Adjust(arr, i, len - 1);}for (int i = 0; i < len - 1; i++)//数据处理{//将根节点和最后一个节点交换int tmp = arr[0];arr[0] = arr[len - 1 - i];arr[len - 1 - i] = tmp;Heap_Adjust(arr, 0, len - 2 - i);//重新构建大顶堆}
}

注：该代码构建为大顶堆。 

 算法分析：

时间复杂度：O（n*logn）

空间复杂度：O（1）

稳定性：不稳定 

八、快速排序

思想：

每次以第一个数为基准数进行比较将数据中比基准数小的数全部放到基准数左边比基准数大的数放到其右边，然后分别对基准数左边和右边的数据分别重复上述操作到有一边的数小于二个为止，重复这一操作到所有的分开部分完成。

动图演示：

代码实现：

int  Partition(int* arr, int left,int right)//单次分配函数返回分配后基准值下标，left为待分配数据最左边数据下标，right为待分配数据最右边数据下标
{int tmp = arr[left];//确认基准值while (left < right)//分配过程{while (arr[right] > tmp && right > left)//从右向左找比基准值小的数{right--;}arr[left] = arr[right];//将从右边找到的比基准值小的数交换到左边while (arr[left] <= tmp && left < right )//从左向右找比基准值大的数{left++;}arr[right] = arr[left];//将从左边找到的比基准值大的数交换到右边}arr[left] = tmp;//将基准值放入空位return left;//返回基准值下标
}
void Quick_Sort(int* arr, int left,int right)
{int mid = Partition(arr, left, right);//先进行一次分配//用递归对分配好后左右边的数据分别进行再分配if (left < mid - 1)Quick_Sort(arr, left, mid - 1);if (right > mid + 1)Quick_Sort(arr, mid + 1, right);
}

注：该代码为快速排序的递归写法。 

void Get_Threemid_Num(int* arr, int left,int right)//快排优化（三数取中法）
{int tmp;//交换中间变量int mid = (left + right) / 2;//这组数据中间数据下标if (arr[left] > arr[mid])//将第一个数与中间一个数较大的数放到中间{tmp = arr[left];arr[left] = arr[mid];arr[mid] = tmp;}if (arr[mid] < arr[right])//在上一步的基础上将最大的数放到中间{tmp = arr[mid];arr[mid] = arr[right];arr[right] = tmp;}if (arr[left] < arr[right])//将三个数中第二大的数放到第一个位置，最小的数放到最后一个位置{tmp = arr[left];arr[left] = arr[right];arr[right] = tmp;}
}
int  Partition(int* arr, int left,int right)//单次分配函数返回分配后基准值下标，left为待分配数据最左边数据下标，right为待分配数据最右边数据下标
{Get_Threemid_Num(arr, left, right);int tmp = arr[left];//确认基准值while (left < right)//分配过程{while (arr[right] > tmp && right > left)//从右向左找比基准值小的数{right--;}arr[left] = arr[right];//将从右边找到的比基准值小的数交换到左边while (arr[left] <= tmp && left < right )//从左向右找比基准值大的数{left++;}arr[right] = arr[left];//将从左边找到的比基准值大的数交换到右边}arr[left] = tmp;//将基准值放入空位return left;//返回基准值下标
}
void Quick_Sort(int* arr, int left, int right)
{std::stack<int> str;//开辟一个栈用来放每一次分配好后的左右部分的left，right//先进行一次分配并将数据存入到栈中使栈不空int mid = Partition(arr, left, right);if (left < mid - 1)//将符合条件的左部分的left，rght写入栈中{str.push(left);str.push(mid - 1);}if (right > mid + 1)//将符合条件的右部分的left，rght写入栈中{str.push(mid + 1);str.push(right);}while (!str.empty())//若栈中有数据则继续执行{//每一次从栈中取出一组left，rightright = str.top();str.pop();left = str.top();str.pop();mid = Partition(arr, left, right);//分配if (left < mid - 1)//将符合条件的左部分的left，rght写入栈中{str.push(left);str.push(mid - 1);}if (right > mid + 1)//将符合条件的右部分的left，rght写入栈中{str.push(mid + 1);str.push(right);}}
}

注：该代码为快速排序栈实现的非递归写法并用“三数取中法”进行了优化（因为C语言栈代码过长这里用了C++库函数的栈）

 算法分析：

时间复杂度：最好情况O（n*logn），最坏情况O（n^2）

空间复杂度：O（logn）

稳定性：不稳定 

---

总结

   这八种基本排序中前三种排序时间复杂度较高，但空间复杂度较低，适合在处理较少数据时使用若对数据的稳定性有要求则应该从冒泡排序和简单插入排序中进行选择。

   后面五种排序较为复杂适合处理较多数据情况，当数据非常乱的情况下适合用快速排序，当数据最高位数较少时适合用基数（桶）排序，当要在较多数据中获取前几个大或小数据时适合用堆排序……

  面对复杂多变的现实情况选择适当的排序方法能够极大简化处理。目前来说快速排序是非常重要的需要着重了解。