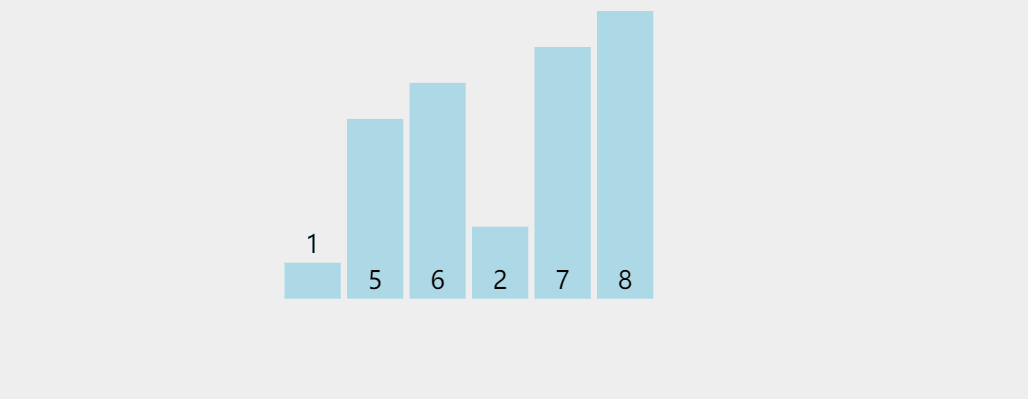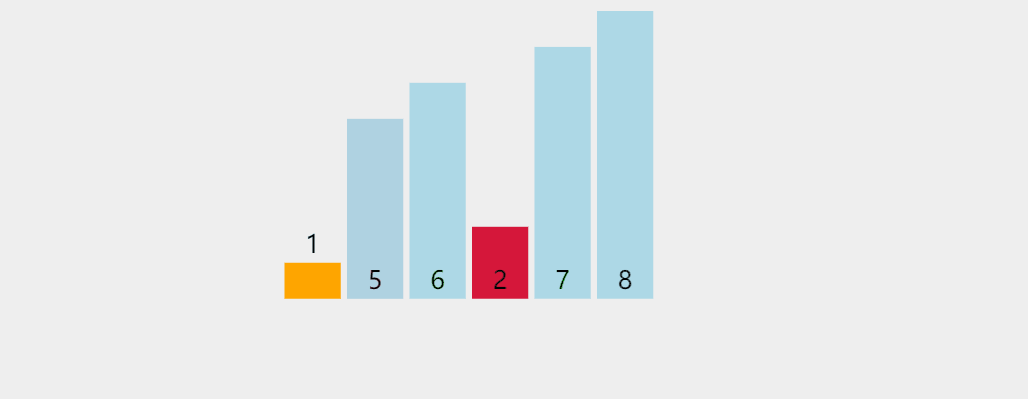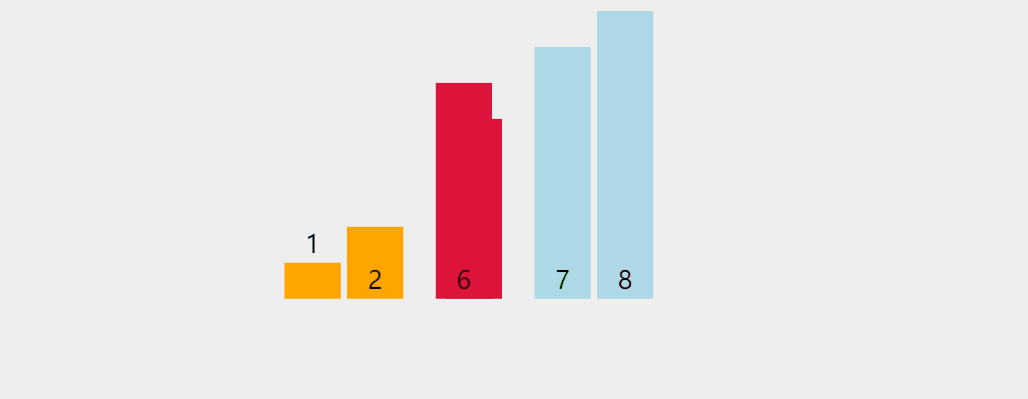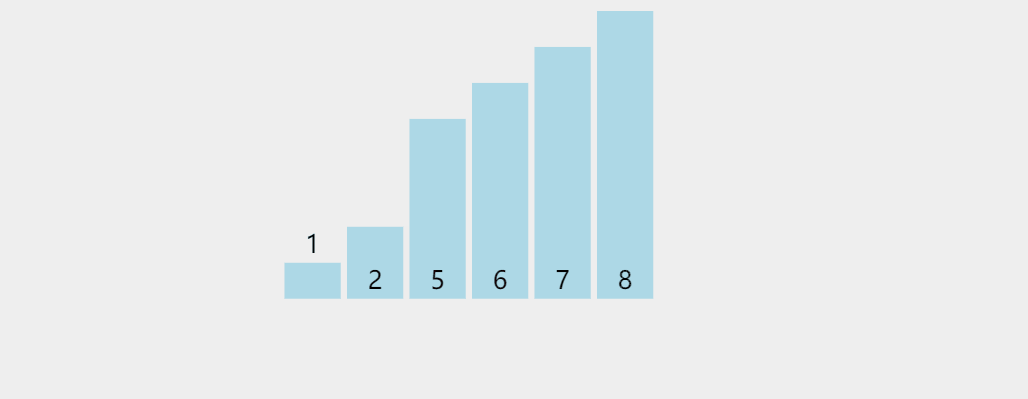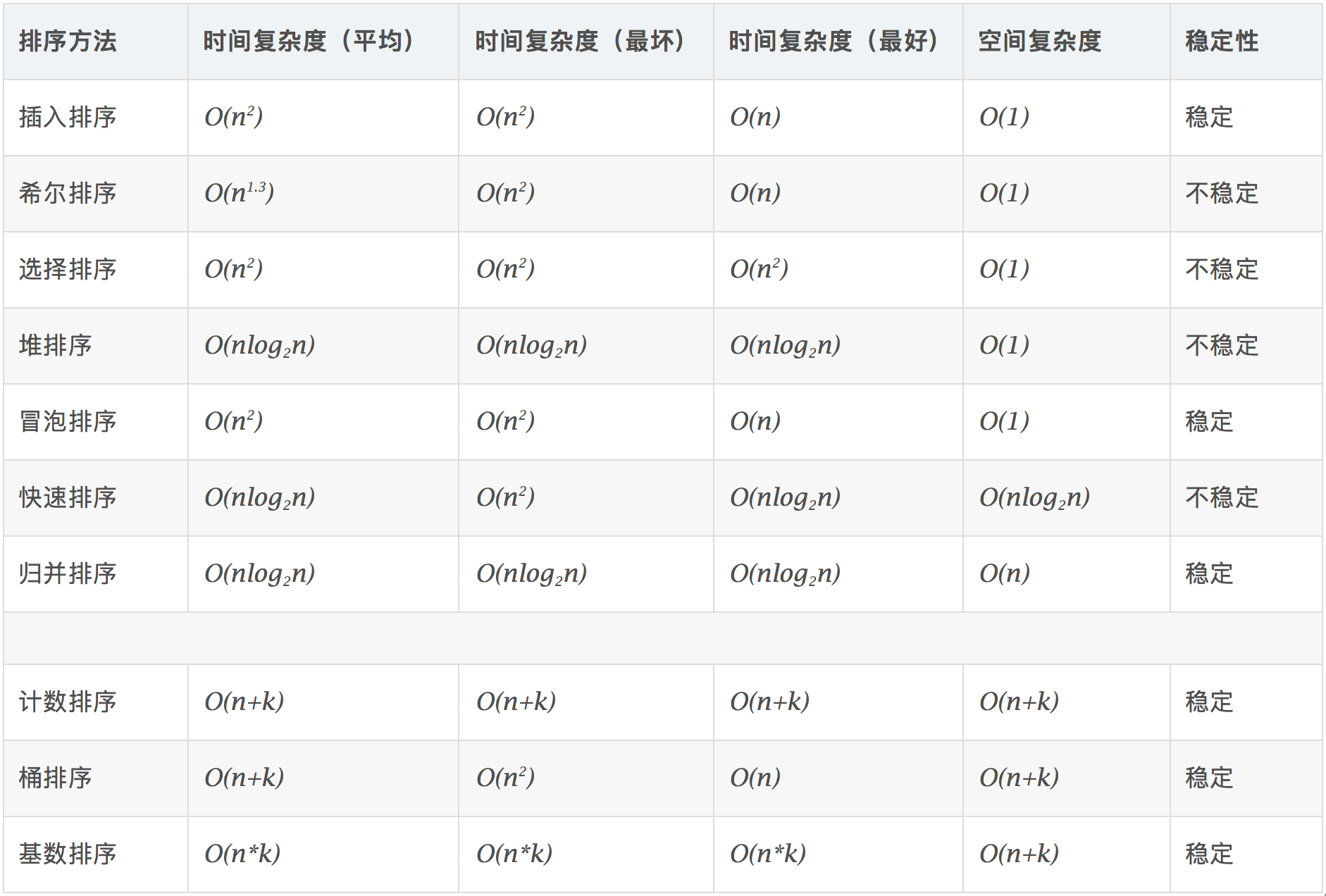
排序算法

平时用惯了高级语言高级工具高级算法，难免对一些基础算法感到生疏。但最基础的排序算法中实则蕴含着相当丰富的优化思维，熟练运用可起到举一反三之功效。

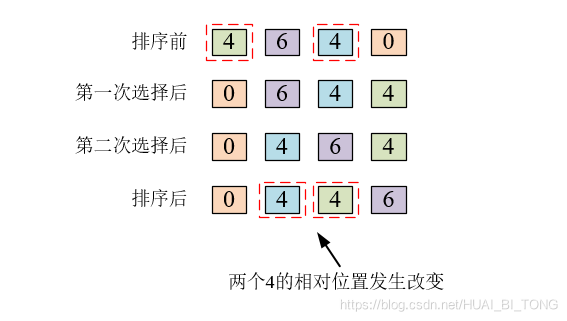
选择排序

选择排序几乎是最无脑的一种排序算法，通过遍历一次数组，选出其中最大（小）的值放在新数组的第一位；再从数组中剩下的数里选出最大（小）的，放到第二位，依次类推。

$\text{算法步骤}$

设数组有$n$个元素， { a 0 , a 1 , … , a n } \{a_0,a_1,\ldots,a_n\} {a0​,a1​,…,an​}

1. 从数组第$i$位开始便利，找到最大值，将之与数组第$i$位交换位置。
2. $i$从0循环到$n$。

由于每次遍历需要计算$O(n)$次，且需要便利$n$次，故时间复杂度为$O(n^2)$；由于只在交换的过程中需要额外的数据，所以空间复杂度为$O(n)$。

C语言实现

//sort.c
void SelectionSort(double *p, int n);
int main(){double test[5] = {3,2,5,7,9};SelectionSort(test,5);for (int i = 0; i < 5; i++)printf("%f\n", test[i]);return 0;
}//交换数组中i,j处的值
void mySwap(double *arr, int i, int j){double temp = arr[i];arr[i] = arr[j];arr[j] = temp;
}//选择排序
void SelectionSort(double *arr, int n){int pMax;double temp;for (int i = 0; i < n-1; i++){pMax = i;for (int j = i+1; j < n; j++)if (arr[j]>arr[pMax])pMax = j;mySwap(arr,pMax,i);}
}

验证

>gcc sort.c
>a
9.000000
7.000000
5.000000
3.000000
2.000000

冒泡排序

冒泡排序也是一种无脑的排序方法，通过重复走访要排序的数组，比较相邻的两个元素，如果顺序不符合要求则交换两个数的位置，直到不需要交换为止。

$\text{算法步骤}$

设数组有$n$个元素， { a 0 , a 1 , … , a n } \{a_0,a_1,\ldots,a_n\} {a0​,a1​,…,an​}

1. 比较相邻的元素$a_i,a_{i+1}$，如果$a_i>a_{i+1}$，则交换二者。
2. 由于每遍历一次都可以将最大的元素排到最后面，所以下一次可以少便利一个元素。
3. 重复遍历数组$n$次

由于每次遍历需要计算$O(n)$次，且需要遍历$n$次，故时间复杂度为$O(n^2)$，空间复杂度为$O(n)$。

C语言实现

//冒泡排序
void BubbleSort(double *arr, int n)
{n = n-1;double temp;for (int i = 0; i < n; i++)for (int j = 0; j < n-i; j++)if (arr[j]>arr[j+1])mySwap(arr,i,j);        /*前文定义的函数*/
}

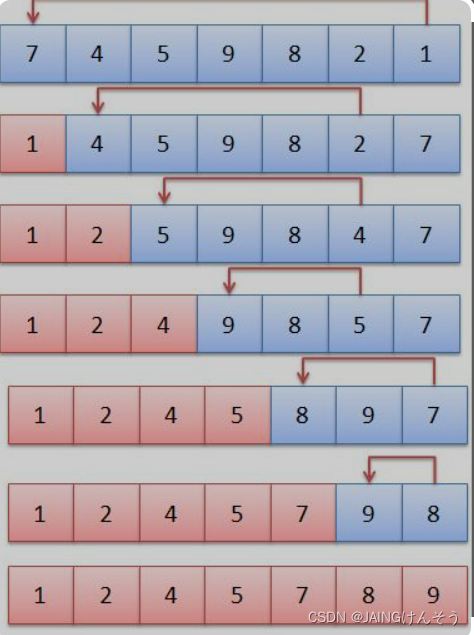
插入排序

插入排序是算法导论中的第一个算法，说明已经不那么无脑了。其基本思路是将数组划分位前后两个部分，前面是有序数组，后面是无序数组。逐个扫描无序数组，将每次扫描的数插入到有序数组中。这样有序数组会越来越长，无序数组越来越短，直到整个数组都是有序的。

$\text{算法步骤}$

设数组有$n$个元素， { a 0 , a 1 , … , a n } \{a_0,a_1,\ldots,a_n\} {a0​,a1​,…,an​}

1. 假设数组中的第0个数已经有序
2. 取出无序数组的第0个元素，将其与有序数组比较，插入到有序数组中。

可见，插入排序的每次插入都有$O(n)$的复杂度，而需要遍历$n$次，所以时间复杂度仍为$O(n^2)$。

C语言实现

//插入排序
void InsertionSort(double *arr, int n){double temp;int j;for (int i = 1; i < n; i++){j = i-1;temp  = arr[i];while (temp<arr[j] && j>=0){arr[j+1] = arr[j];      //第j个元素后移j--;}arr[j+1] = temp;}
}

归并排序

归并排序是算法导论中介绍分治概念时提到的一种排序算法，其基本思路为将数组拆分成子数组，然后令子数组有序，再令数组之间有序，则可以使整个数组有序。

$\text{算法步骤}$

设数组有$n$个元素， { a 0 , a 1 , … , a n } \{a_0,a_1,\ldots,a_n\} {a0​,a1​,…,an​}

1. 如果数组元素大于2，则将数组分成左数组和右数组，如果数组等于2，则将数组转成有序数组
2. 对左数组和右数组执行1操作。
3. 合并左数组和右数组。

可以发现，对于长度为$n$的数组，需要${\log }_{2}n$次的拆分，每个拆分层级都有$O(n)$的时间复杂度和$O(n)$的空间复杂度，所以其时间复杂度和空间复杂度分别为$O(n{\log }_{2}n)和O(n)$

C语言实现

首先考虑两个有序数组的合并问题

//sort.cvoid myMerge(double *arr, int nL, int nR);
int main(){int n = 6;double arr[6] = {2,4,5,1,3,7};Merge(arr,3,3);for (int i = 0; i < n; i++)printf("%f\n", arr[i]);return 0;
}//两个有序数组的混合,arr为输入数组
//nL、nR分别为左数组和右数组的长度
void Merge(double *arr, int nL, int nR){nL = nL-1;                    //左侧最后一个元素的索引int sInsert = 0;               //左侧待插入起始值double temp;for (int i = 1; i <= nR; i++){while (arr[nL+i]>arr[sInsert])sInsert++;if (sInsert<nL+i){temp = arr[nL+i];for (int j = nL+i; j > sInsert; j--)arr[j]=arr[j-1];arr[sInsert] = temp; }elsebreak;    //如果sInsert==nL+i，说明右侧序列无需插入}
}

验证

> gcc sort.c
> a
1.000000
2.000000
3.000000
4.000000
5.000000
7.000000

然后考虑归并排序的递归过程

void MergeSort(double *arr, int n);
void myMerge(double *arr, int nL, int nR);int main(){int n = 6;double arr[6] = {5,2,4,7,1,3};MergeSort(arr,n);for (int i = 0; i < n; i++)printf("%f\n", arr[i]);return 0;
}void MergeSort(double *arr, int n){if (n>2){int nL = n/2;int nR = n-nL;MergeSort(arr,nL);MergeSort(arr+nL,nR);Merge(arr,nL,nR);}else if(n==2)Merge(arr,1,1);//当n==1时说明数组中只剩下一个元素，所以什么也不用做
}

验证

> gcc sort.c
> a
1.000000
2.000000
3.000000
4.000000
5.000000
7.000000

至此，排序算法终于有一点算法的味道了。

希尔排序

据说是第一个突破$O(n^2)$的排序算法，又称为缩小增量排序，本质上也是一种分治方案。

在归并排序中，先将长度为n的数组划分为长度为nL和nR的两个数组，然后继续划分，直到每个数组的长度不大于2，再对每个不大于2的数组进行排序。这样，每个子数组内部有序而整体无序，然后将有序的数组进行回溯重组，直到重新变成长度为n的数组为止。

希尔排序的划分策略则不然，这里在将数组划分为nL和nR之后，对nR和nR进行按位排序，使得nL和nR内部无序，但整体有序。然后再将数组进行细分，当数组长度变成1的时候，内部也就谈不上无序了，而所有长度为1的数组整体有序，也就是说有这些子数组所组成的数组是有序的。

$\text{算法步骤}$

设数组有$n$个元素， { a 0 , a 1 , … , a n } \{a_0,a_1,\ldots,a_n\} {a0​,a1​,…,an​}

1. 如果数组元素大于2，则将数组分成左数组和右数组，并对左数组和右数组的元素进行一对一地排序。
2. 对每一个数组进行细分，然后将每个子数组进行一对一地排序。

C语言实现

//希尔排序
void ShellSort(double *arr, int n){double temp;int j;for (int nSub = n/2; nSub >0; nSub/=2)      //nSub为子数组长度for (int i = nSub; i < n; i++){temp = arr[i];for (j = i-nSub; j >= 0&& temp<arr[j]; j -= nSub)arr[j+nSub] = arr[j];arr[j+nSub] = temp;}
}

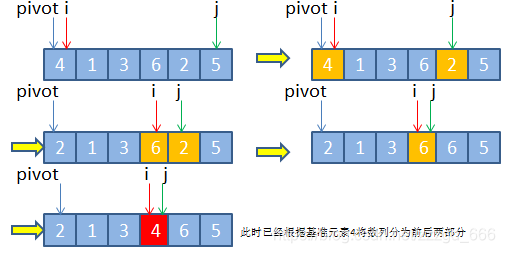
快速排序

快速排序的分治策略与希尔排序类似，其核心思想都是从组内无序而组间有序出发，当子数组长度缩减至1的时候，则整个数组便是有序的。

$\text{算法步骤}$

设数组有$n$个元素， { a 0 , a 1 , … , a n } \{a_0,a_1,\ldots,a_n\} {a0​,a1​,…,an​}

1. 在数组中随机选出一个基准$a_{mid}$
2. 通过$a_{mid}$将数组分成两部分，其中左边小于$a_{mid}$，右边大于$a_{mid}$。
3. 对左右子数组重复1、2操作，直到子数组长度为1。

由于快速排序的过程中有一个随机选择，所以其时间复杂度可能会受到这个随机选择的影响，如果运气不好的话，快速排序可能会变成冒泡排序。当然，一般来说运气不会那么差，快速排序的平均时间复杂度为$O(n{\log }_{2}n)$。

C语言实现

//快速排序
void QuickSort(double *arr, int n){double pivot = arr[0];      //选取第0个点为基准int i = 1;int j = n-1;while (i<j){if (arr[i]<pivot)i++;else{mySwap(arr,i,j);j--;}}if (arr[i]>pivot)i--;mySwap(arr,i,0);if (i>1)QuickSort(arr,i);    //对i前的数组进行快排i++;if (i<n-1)QuickSort(arr+i,n-i);//对i+1后的数组进行快排
}

堆排序

堆是算法导论中介绍的第一种数据结构，本质是一种二叉树，最大堆要求子节点的值不大于父节点，最小堆反之。由于堆是一种带有节点的数据结构，所以结构表示更加直观。好在二叉树父子节点的序号之间存在简单的递推关系，所以在C语言中可以用数组表示堆，

根据上图可知，若父节点的序号为$n$，则左子节点序号为$2n+1$,右子节点序号为$2n+2$。

可以将上图理解为一个排好序的最小堆，如果1位变成15，那么此时这个节点将违反最小堆的原则，经过比对，应该调换15和3的位置。调换之后，15仍然比7和8大，则再调换15和7的位置，则这个最小堆变为

从而继续满足最小堆的性质，最大堆亦然，其C语言实现为

//如果堆中节点号为m的点不满足要求，则调整这个点
//此为最大堆
void adjustHeap(double *arr, int m, int n){int left = m*2+1;       //左节点while (left<n){if (left+1<n)       //判断右节点if (arr[left]<arr[left+1])left++;     //当右节点大于左节点时，left表示右节点if (arr[m]>arr[left])break;          //如果父节点大于子节点，则说明复合最大堆else{mySwap(arr,m,left);m = left;left = m*2+1;}}
}

堆的调整过程就是父节点与其左右两个子节点比较的过程，也就是说通过这种方式得到的堆能够满足父子节点的大小关系，但两个孙节点之间并不会被排序。但是，如果一个数组已经满足最大堆要求，那么只需让所有的节点都在根节点处重新参与排序，那么最终得到的最大堆一定满足任意节点间的有序关系。

//堆排序
void HeapSort(double *arr, int n){for (int i = n/2; i >= 0; i--)adjustHeap(arr,i,n);        //初始化堆for (int i = n-1; i > 0 ; i--){mySwap(arr,0,i);            //将待排序元素放到最顶端adjustHeap(arr,0,i);        //调整最顶端的值 }   
}

计数排序

此前所有的排序算法均没有考虑到数组的内在分布，如果我们输入的数据为某个区间内的整数，那么我们只需建立这个区间内的整数索引，然后将每个数归类到这个索引之中即可。

这便是桶排序的思路，所谓桶排序即通过将已知数据划分为有序的几个部分，放入不同的桶中，这个分部过程即桶排序。除了计数排序，基数排序是一种更广泛的桶排序形式，其划分方式可以为数据的位数，把这个桶定义为数据最高位的值。

例如，我们有一组均匀分布在$[0,100]$之内的数据，所谓基数排序，即先划分出十个不同的桶$[0,10),[10,20),\dots ,[90,100)$，然后再对每个桶进行单独的排序。这样划分下去，那么基数排序的复杂度则为$O(10\ast n)$。

词典中的排序方式也可以理解为一种基数排序，即首先看第一个字母的顺序，然后第二个，依次类推。由于桶排序对数据做了假设，所以其最优时间复杂度可以达到$O(n+k),k$为桶的数目。

例如，我们有一个由一百个由1和2组成的数组，那么我们只需建立一个索引$1:n_1,2:n_2$，然后统计1和2分别出现的个数即可，其时间复杂度也将变成$O(n)$。

在这里只做出最简单的计数排序。

/计数排序,输入数组为整数
void CountingSort(int *arr,int n){int aMax = arr[0];int aMin = arr[0];for (int i = 0; i < n; i++) //查找最大值和最小值if (arr[i]>aMax)aMax = arr[i];else if (arr[i]<aMin)aMin = arr[i];int m = aMax-aMin+1;         //索引长度int *arrSort = (int*)malloc(sizeof(int)*m);for (int i = 0; i < m; i++)arrSort[i]=0;           //初始化索引for (int i = 0; i < n; i++) //排序arrSort[arr[i]-aMin] += 1;n = 0;for (int i = 0; i < m; i++){aMax = i+aMin;          //此值为真实数据for (int j = n; j < n+arrSort[i]; j++)arrSort[j] = i+aMin;n += arrSort[i];}
}