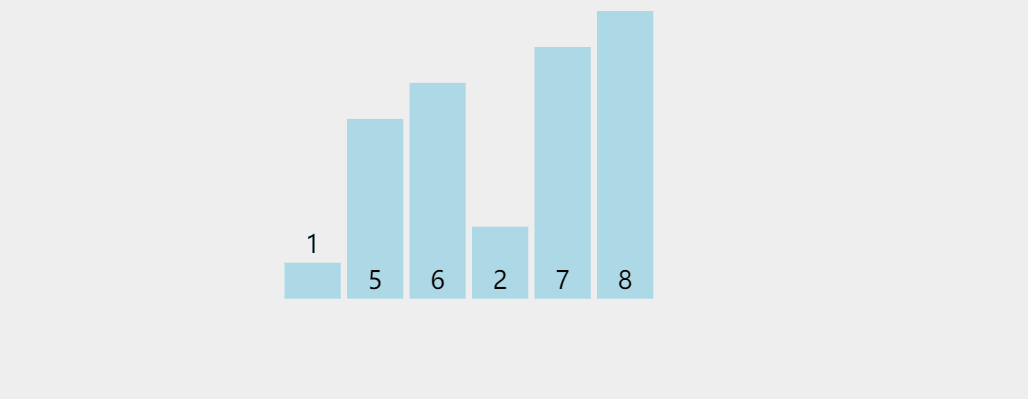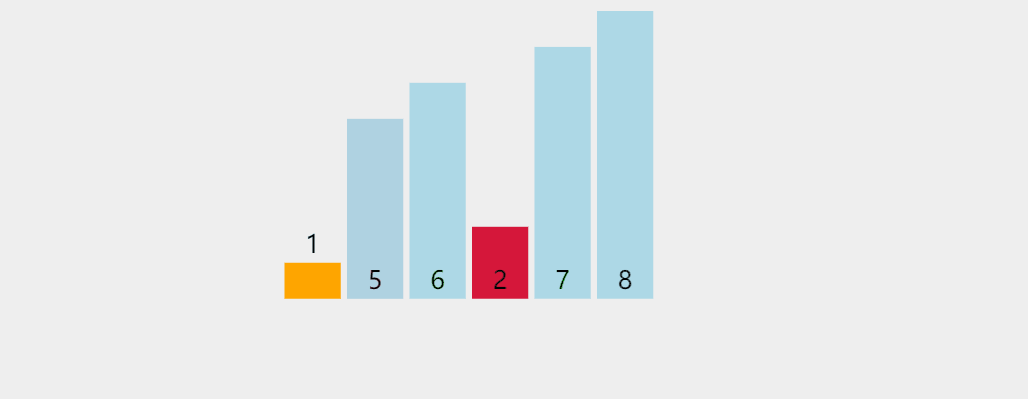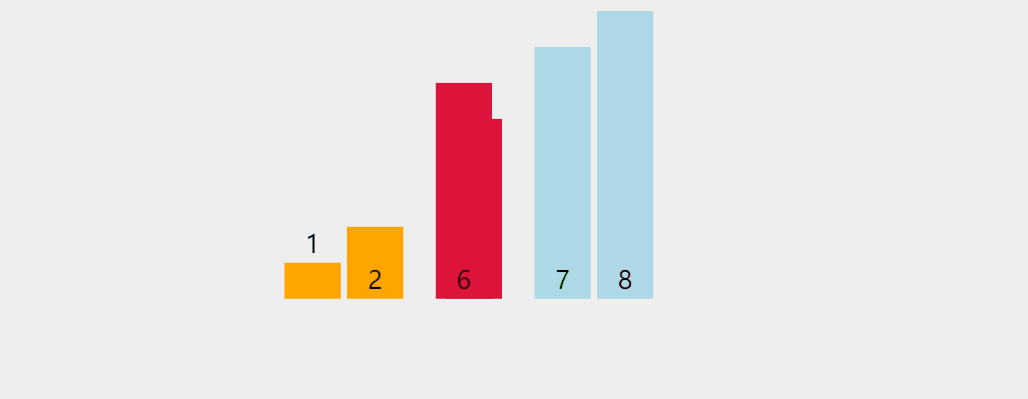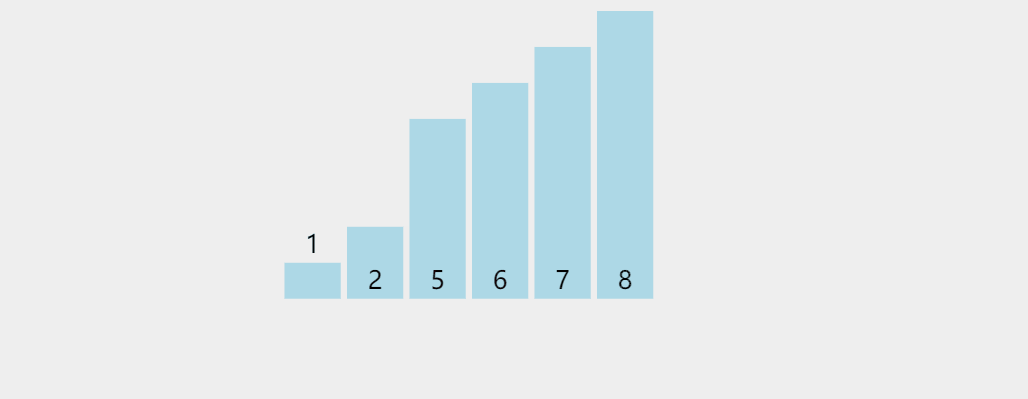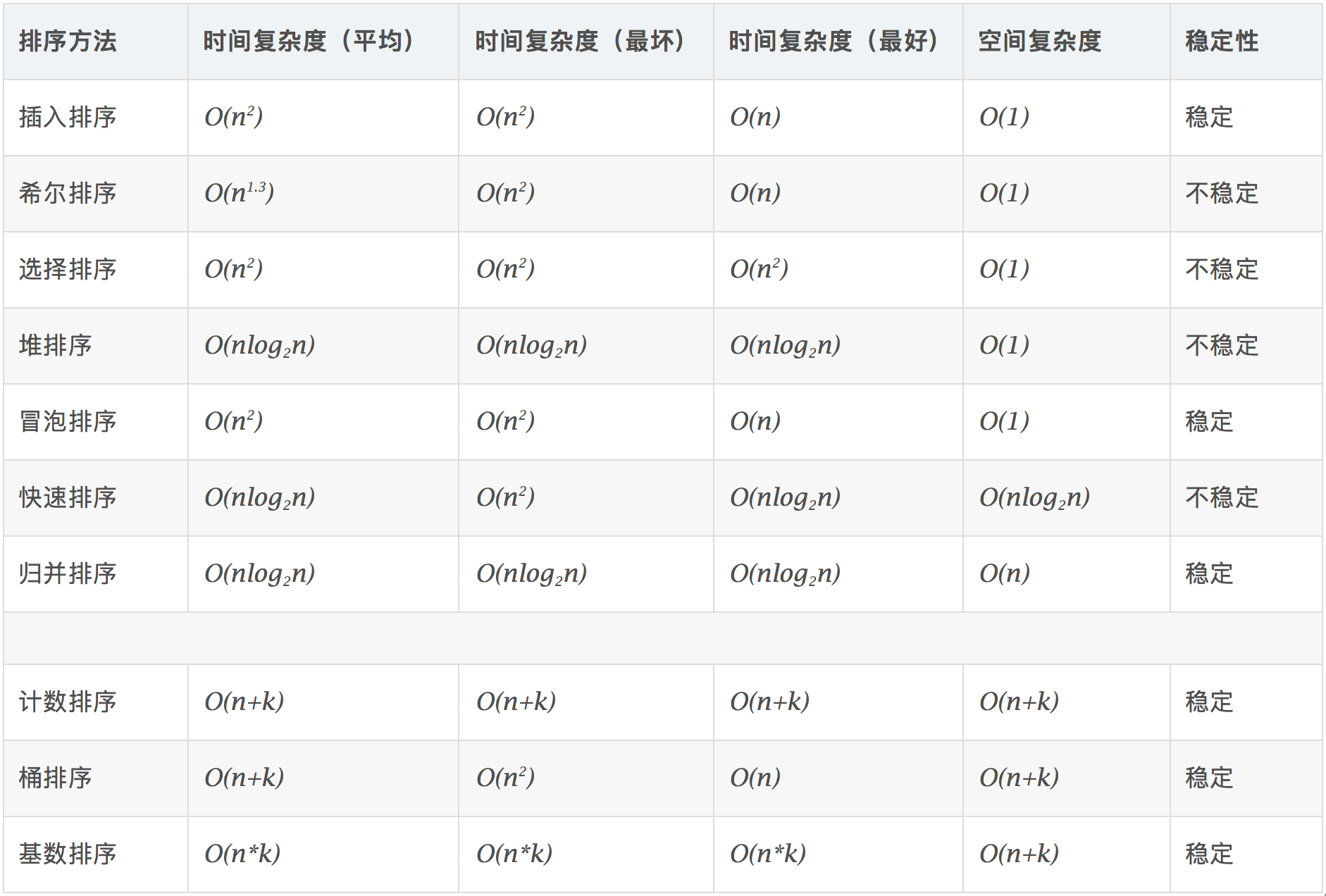
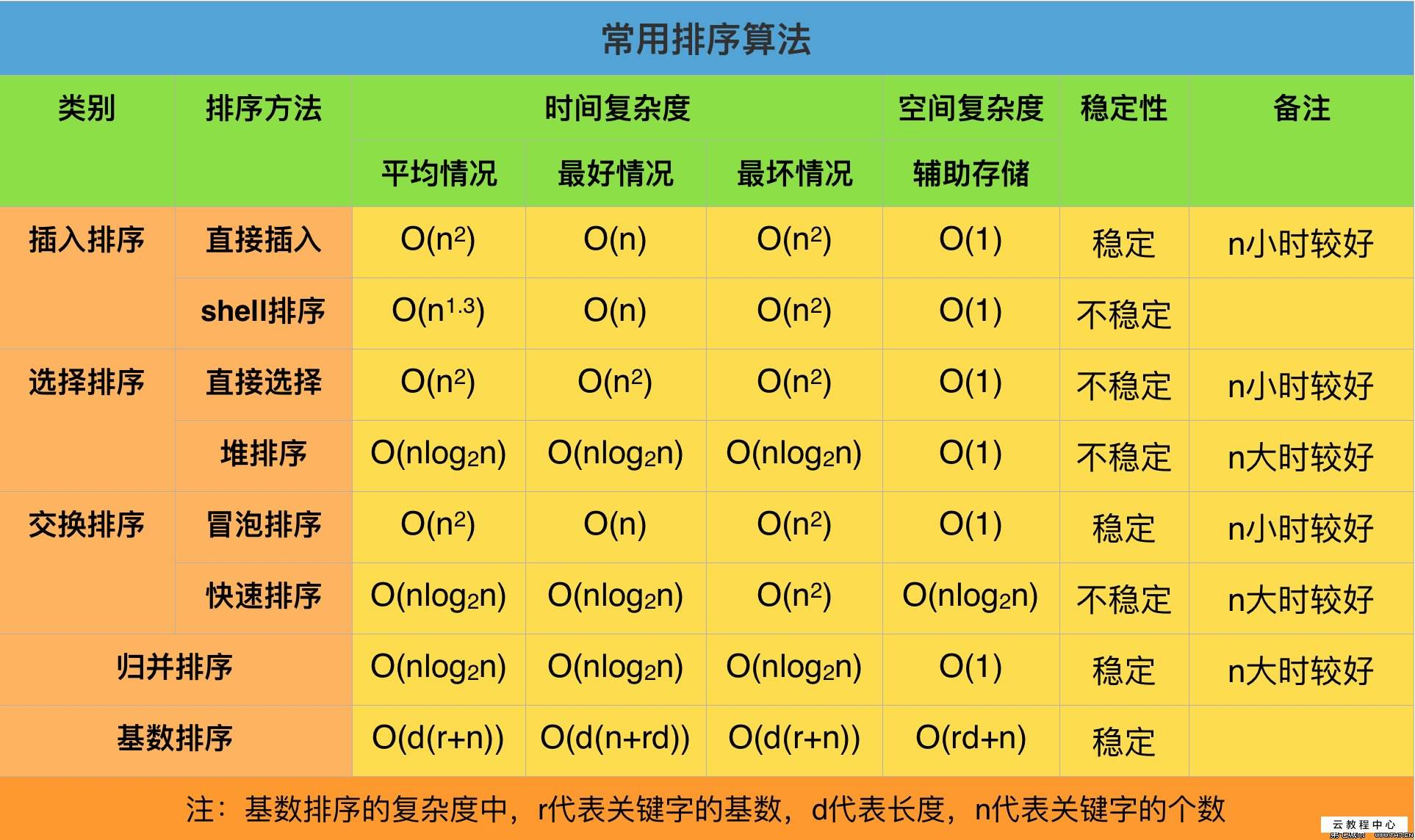
排序算法概述

  所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。排序算法，就是如何使得记录按照要求排列的方法。排序算法在很多领域得到相当地重视，尤其是在大量数据的处理方面。一个优秀的算法可以节省大量的资源。在各个领域中考虑到数据的各种限制和规范，要得到一个符合实际的优秀算法，得经过大量的推理和分析。

一：冒泡排序（Bubble Sort）

 1、冒泡排序简要概述

  冒泡排序（BubbleSorting）的基本思想是：通过对待排序序列从前向后（从下标较小的元素开始）,依次比较相邻元素的值，若发现逆序则交换，使值较大的元素逐渐从前移向后部。
  因为排序的过程中，各元素不断接近自己的位置，如果一趟比较下来没有进行过交换，就说明序列有序，因此要在排序过程中设置一个标志flag判断元素是否进行过交换。从而减少不必要的比较。

 2、冒泡排序图解

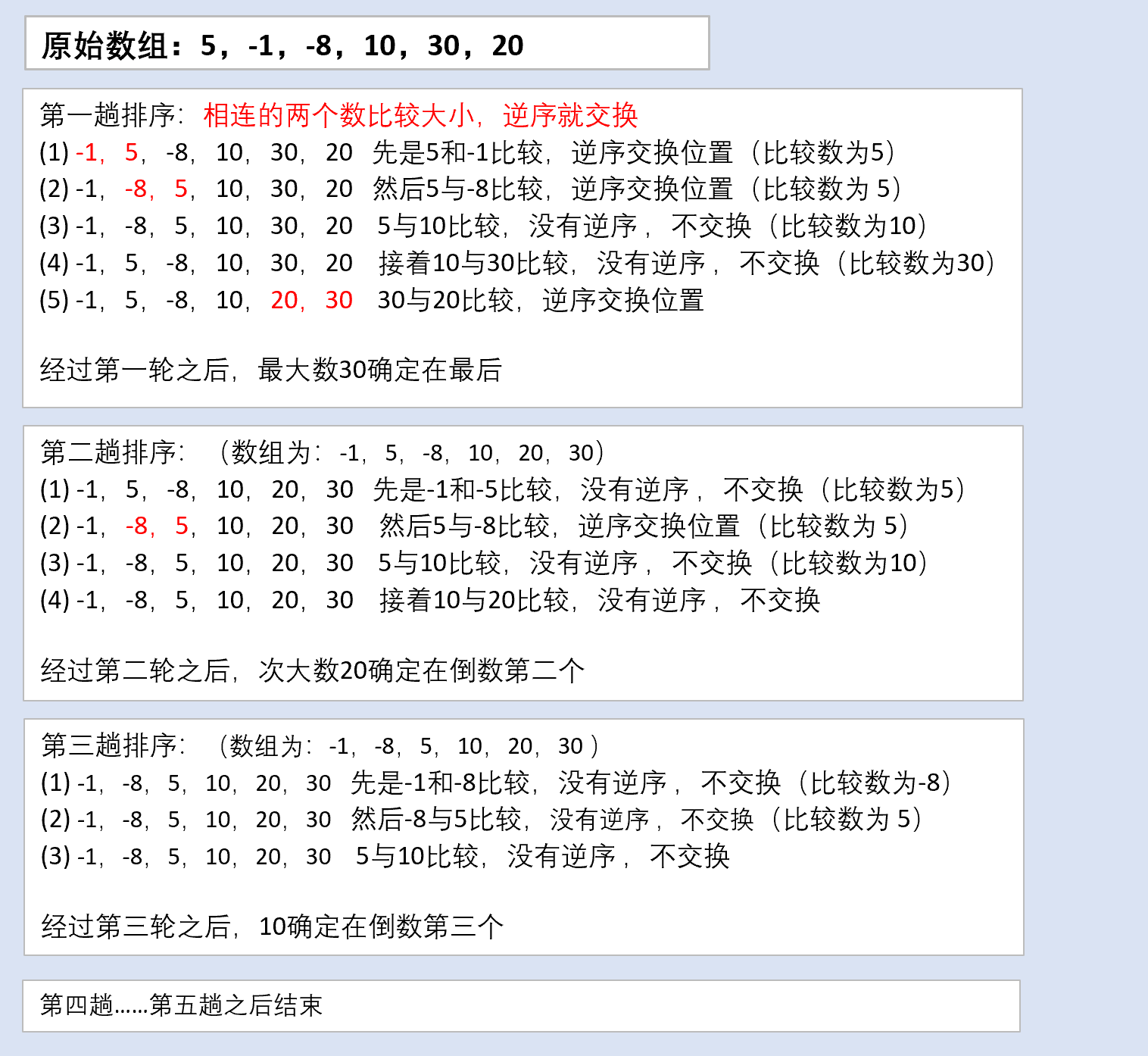
总结：
(1)一共进行（数组的大小-1）次大的循环
(2)每一趟排序的次数在逐渐的减少
(3)如果我们发现在某趟排序中，没有发生一次交换，可以提前结束冒泡排序。（优化）

 3、代码实现

#include <stdio.h>
int main(int argc, char *argv[])
{void bubbleSort(int a[],int len);int arr[]={5, -1, -8, 10, 30, 20};//得到数组的长度 int length=sizeof(arr)/sizeof(arr[0]);printf("冒泡排序前：");for (int i = 0; i < length; i++) {printf("%d ",arr[i]);}bubbleSort(arr,length);printf("\n");printf("冒泡排序后：");for (int i = 0; i < length; i++) {printf("%d ",arr[i]);}printf("\n");return 0;
}
void bubbleSort(int a[],int len){int temp = 0;for (int i = 0; i < len; i++) {for (int j = 0; j < len - 1; j++) {if (a[j] > a[j + 1]) {temp = a[j];a[j] = a[j + 1];a[j + 1] = temp;}}}
}

结果如下：

二：选择排序（Select Sort）

 1、选择排序简要概述

  它的基本思想是：第一次从arr[0]到arr[n-1]中选取最小值，与arr[0]交换，第二次从arr[1]到arr[n-1]中选取最小值，与arr[1]交换，第三次从arr[2]到arr[n-1]中选取最小值，与arr[2]交换，…，第i次从arr[i-1]到arr[n-1]中选取最小值，与arr[i-1]交换，…,第n-1次从arr[n-2]~arr[n-1]中选取最小值，与arr[n-2]交换，
  总共通过n-1次，得到一个按排序码从小到大排列的有序序列。

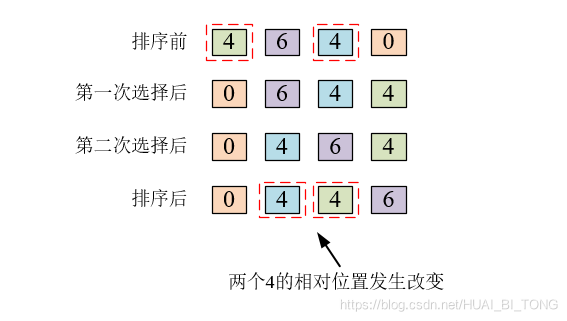
 2、选择排序图解

 3、代码实现

#include <stdio.h>
int main(int argc, char *argv[])
{void selectSort(int a[],int len);int arr[]={5, -1, -8, 10, 30, 20};//得到数组的长度 int length=sizeof(arr)/sizeof(arr[0]);printf("选择排序前：");for (int i = 0; i < length; i++) {printf("%d ",arr[i]);}selectSort(arr,length);printf("\n");printf("选择排序后：");for (int i = 0; i < length; i++) {printf("%d ",arr[i]);}printf("\n");return 0;
}
void selectSort(int a[],int len){int temp = 0;for (int i = 0; i < len - 1; i++) {int minIndex = i;int min = a[minIndex];for (int j = i + 1; j < len; j++) {if (min > a[j]) { min = a[j];minIndex = j;}}if (minIndex != i) {a[minIndex] = a[i];a[i] = min;}}
}

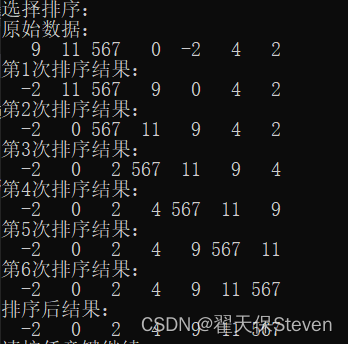
结果如下：

三：插入排序（Insert Sort）

 1、插入排序简要概述

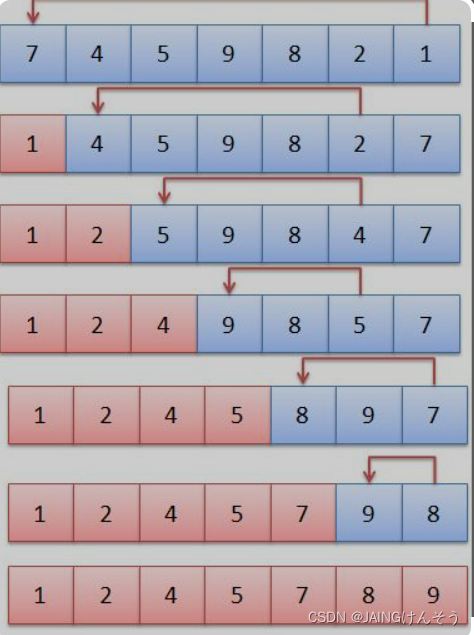
  它的基本思想是：把n个待排序的元素看成为一个有序表和一个无序表，开始时有序表中只包含一个元素，无序表中包含有n-1个元素，排序过程中每次从无序表中取出第一个元素，把它的排序码依次与有序表元素的排序码进行比较，将它插入到有序表中的适当位置，使之成为新的有序表。

 2、插入排序图解

 3、代码实现

#include <stdio.h>
int main(int argc, char *argv[])
{void insertSort(int a[],int len);int arr[]={5, -1, -8, 10, 30, 20};//得到数组的长度 int length=sizeof(arr)/sizeof(arr[0]);printf("直接插入排序前：");for (int i = 0; i < length; i++) {printf("%d ",arr[i]);}insertSort(arr,length);printf("\n");printf("直接插入排序后：");for (int i = 0; i < length; i++) {printf("%d ",arr[i]);}printf("\n");return 0;
}
void insertSort(int a[],int len){int insertVal = 0;   //待插入的值int insertIndex = 0; //待插入的下标for (int i = 1; i < len; i++) {insertVal = a[i];insertIndex = i - 1;while (insertIndex >= 0 && insertVal < a[insertIndex]) {a[insertIndex + 1] = a[insertIndex];insertIndex--;}a[insertIndex + 1] = insertVal;}
}

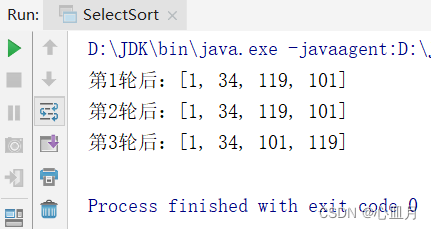
结果如下：

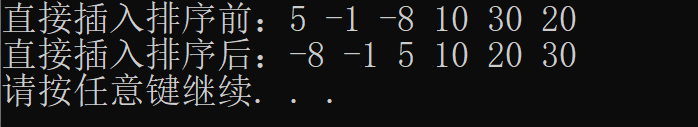
四：希尔排序（Shell Sort）

 1、简单插入排序存在的问题

数组arr={2,3,4,5,6,1}这时需要插入的数1(最小),这样的过程是：

{2,3,4,5,6,6}
{2,3,4,5,5,6}
{2,3,4,4,5,6}
{2,3,3,4,5,6}
{2,2,3,4,5,6}
{1,2,3,4,5,6}

结论：当需要插入的数是较小的数时，后移的次数明显增多，对效率有影响

 2、希尔排序简要概述

  （1）它是简单插入排序经过改进之后的一个更高效的版本，也称为缩小增量排序。
  （2）希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。

 3、希尔排序图解

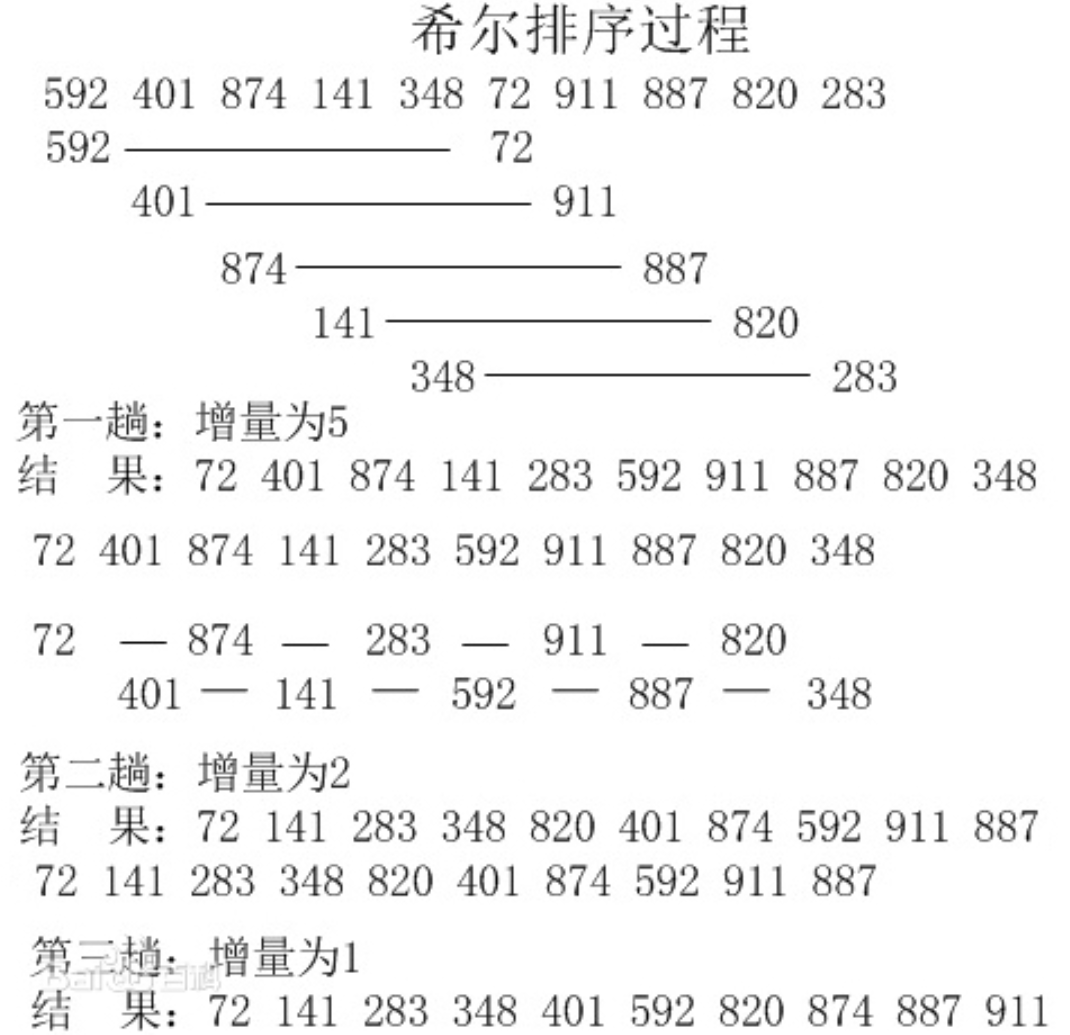
###  4、代码实现

#include <stdio.h>
int main(int argc, char *argv[])
{void shellSort(int a[],int len);int arr[]={5, -1, -8, 10, 30, 20};//得到数组的长度 int length=sizeof(arr)/sizeof(arr[0]);printf("希尔排序前：");for (int i = 0; i < length; i++) {printf("%d ",arr[i]);}shellSort(arr,length);printf("\n");printf("希尔排序后：");for (int i = 0; i < length; i++) {printf("%d ",arr[i]);}printf("\n");return 0;
}
void shellSort(int a[],int len){for (int gap = len / 2; gap > 0; gap /= 2) {for (int i = gap; i < len; i++) {int insertIndex = i;int insertVal = a[insertIndex];if (a[insertIndex] < a[insertIndex - gap]) {while (insertIndex - gap >= 0 && insertVal < a[insertIndex - gap]) {a[insertIndex] = a[insertIndex - gap];insertIndex -= gap;}a[insertIndex] = insertVal;}}}
}

结果如下：

五：快速排序（Quick Sort）

 1、快速排序简要概述

  （1）快速排序（Quicksort）是对冒泡排序的一种改进。
  （2）基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

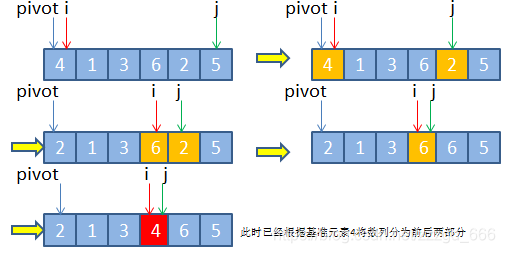
 2、快速排序图解

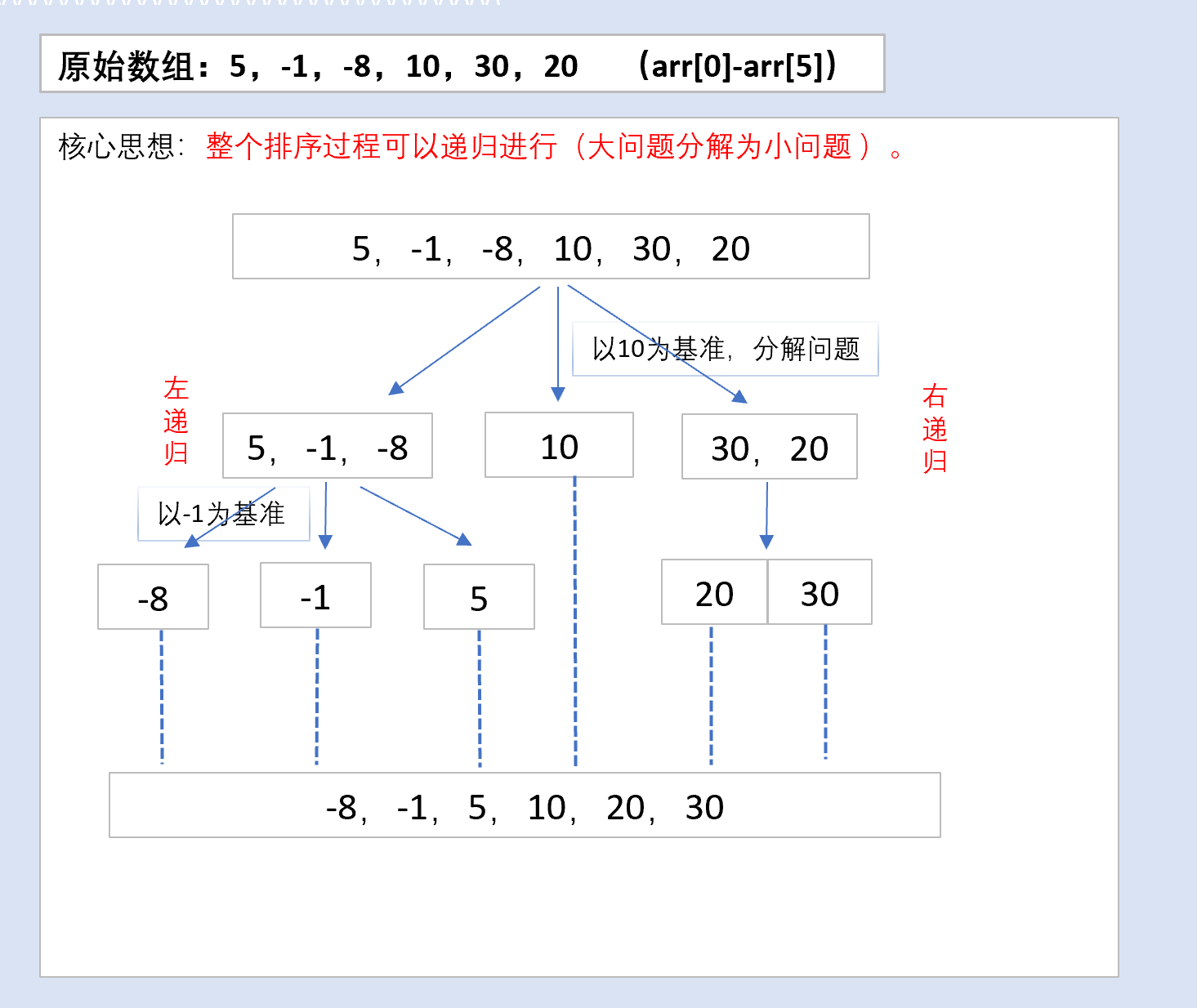
 3、代码实现

#include <stdio.h>
int main(int argc, char *argv[])
{void quickSort(int a[],int left,int right);int arr[]={5, -1, -8, 10, 30, 20};//得到数组的长度 int length=sizeof(arr)/sizeof(arr[0]);printf("快速排序前：");for (int i = 0; i < length; i++) {printf("%d ",arr[i]);}quickSort(arr,0,length - 1);printf("\n");printf("快速排序后：");for (int i = 0; i < length; i++) {printf("%d ",arr[i]);}printf("\n");return 0;
}
void quickSort(int a[],int left, int right){int l = left;int r = right;int midVal = a[(left + right) / 2];int temp = 0;while (r > l) {while (midVal > a[l]) {l += 1;}while (midVal < a[r]) {r -= 1;}if (l >= r) {break;}temp = a[l];a[l] = a[r];a[r] = temp;if (a[r] == midVal) {l++;}if (a[l] == midVal) {r--;}}if (l == r) {l += 1;r -= 1;}if (left < r) {quickSort(a, left, r);}if (right > l) {quickSort(a, l, right);}
}

结果如下：

六：归并排序（merge sort）

 1、归并排序简要概述

  （1）归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。

 2、归并排序图解

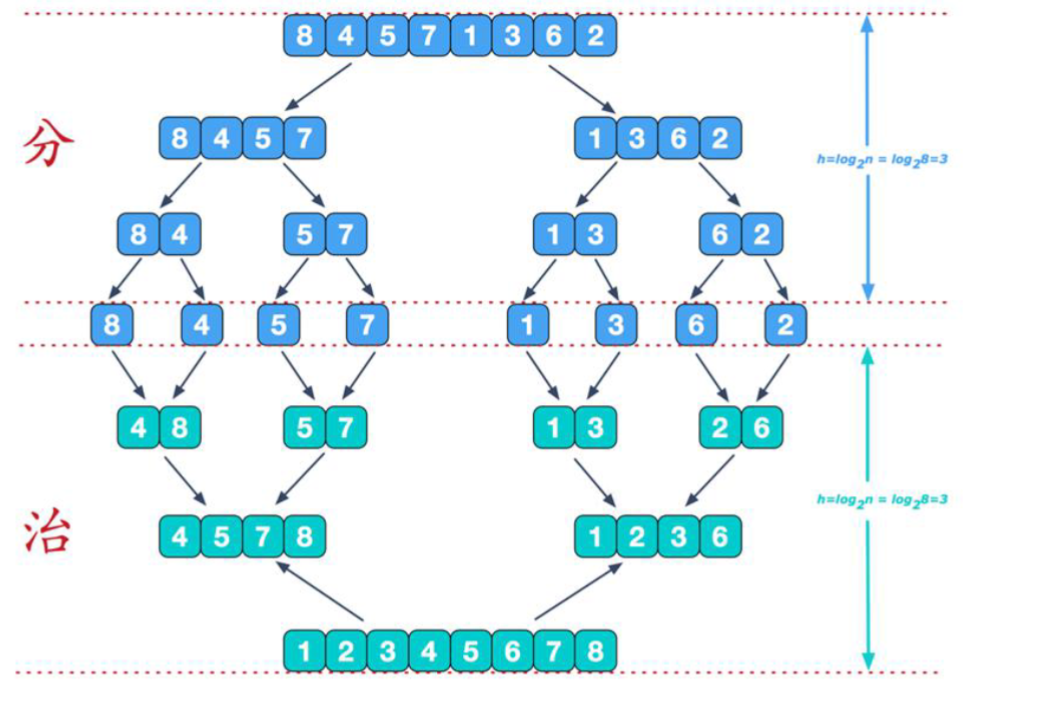
  治阶段，我们需要将两个已经有序的子序列合并成一个有序序列，比如上图中的最后一次合并，要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列，合并为最终序列[1,2,3,4,5,6,7,8]，来看下实现步骤：

 3、代码实现

#include <stdio.h>
int main(int argc, char *argv[])
{void merge(int a[], int left, int right, int mid, int temp[]);void mergeSort(int a[], int left, int right, int temp[]);int arr[]={8, 4, 5, 7, 1, 3, 6, 2};//得到数组的长度 int length=sizeof(arr)/sizeof(arr[0]);int temp[length];printf("快速排序前：");for (int i = 0; i < length; i++) {printf("%d ",arr[i]);}mergeSort(arr, 0, length - 1, temp);printf("\n");printf("快速排序后：");for (int i = 0; i < length; i++) {printf("%d ",arr[i]);}printf("\n");return 0;
}
void merge(int a[], int left, int right, int mid, int temp[]){int i = left;int j = mid + 1;int t = 0;  //指向temp数组while (i <= mid && j <= right) {if (a[i] <= a[j]) {temp[t] = a[i];t += 1;i += 1;} else {temp[t] = a[j];t += 1;j += 1;}}while (i <= mid) {temp[t] = a[i];t += 1;i += 1;}while (j <= right) {temp[t] = a[j];t += 1;j += 1;}t = 0;int tempLeft = left;while (tempLeft <= right) {a[tempLeft] = temp[t];t++;tempLeft++;}
}
void mergeSort(int a[], int left, int right, int temp[]){void merge(int a[], int left, int right, int mid, int temp[]);int mid = 0;if (left < right) {mid = (left + right) / 2;//向左递归mergeSort(a, left, mid, temp);//向右递归mergeSort(a, mid + 1, right, temp);//合并merge(a, left, right, mid, temp);}
}

结果如下：

七：基数排序（radix sort）

 1、基数排序简要概述

  （1）基数排序（radix sort）属于“分配式排序”（distribution sort），又称“桶子法”（bucketsort）或binsort，它是通过键值的各个位的值，将要排序的元素分配至某些“桶”中，达到排序的作用。
  （2）将所有待比较数值统一为同样的数位长度，数位较短的数前面补零。然后，从最低位开始，依次进行一次排序。这样从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。

 2、基数排序图解

  注意：先判断有无负数，有负数时处理思路：有则找到最小值，数组所有数据都减去该值，也就是数组最小值会变为0，接下来按正整数排序，最后数组所有数据加上原最小数，变为原有数据值。
基数排序图解：

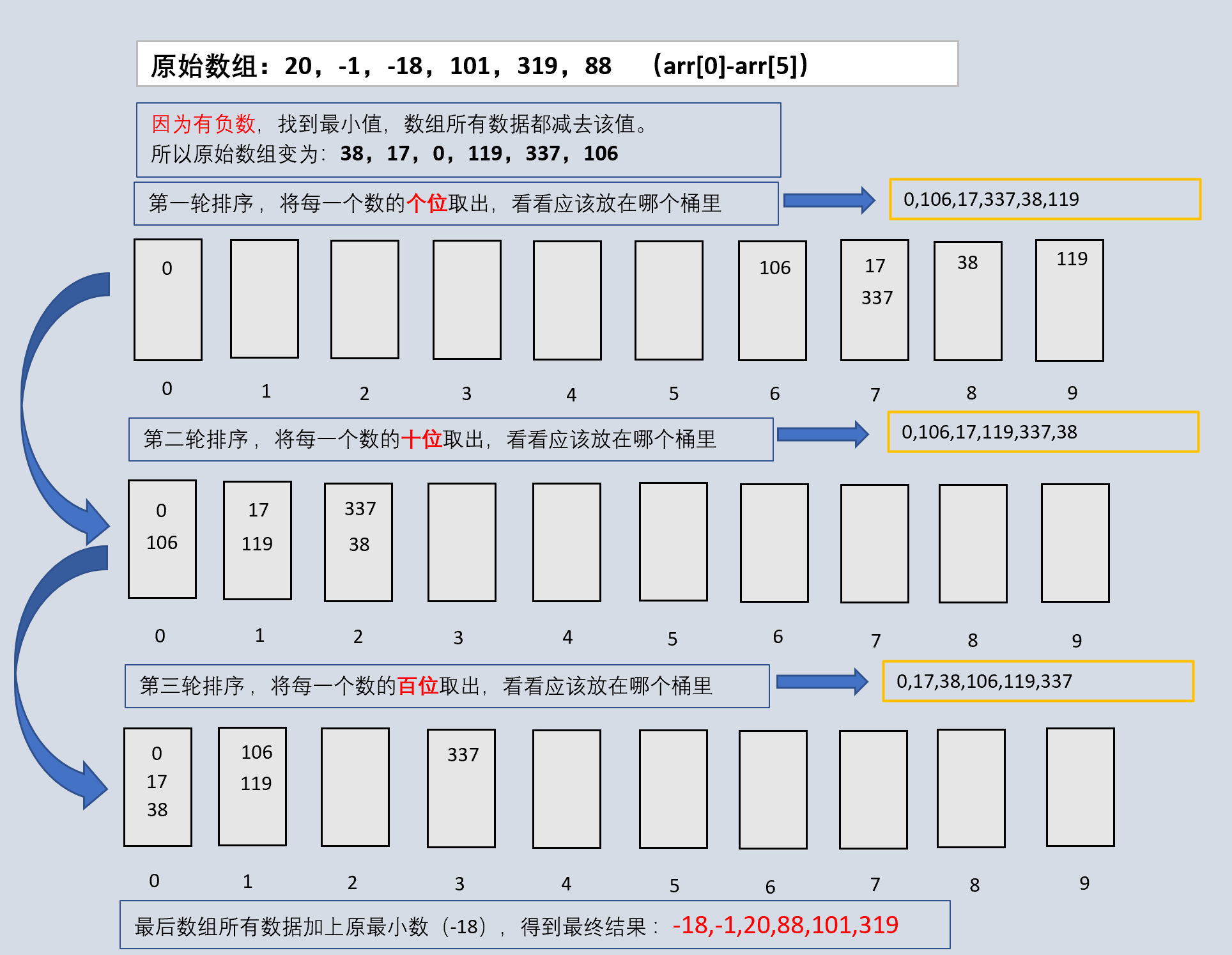
 3、代码实现(不包含负数）

#include <stdio.h>
int main(int argc, char *argv[])
{void radixSort(int a[],int len);int arr[]={20, 1, 18, 101, 319, 88};//得到数组的长度 int length=sizeof(arr)/sizeof(arr[0]);printf("基数(桶)排序前：");for (int i = 0; i < length; i++) {printf("%d ",arr[i]);}radixSort(arr,length);printf("\n");printf("基数(桶)排序后：");for (int i = 0; i < length; i++) {printf("%d ",arr[i]);}printf("\n");return 0;
}
void radixSort(int a[],int len){//用二维数组来表示桶int bucket[10][len] ;//记录最大数的位数int maxLength=0;//用一维数组来表示桶中元素的个数//比如eleCounts[0]记录第0个桶中元素的个数int eleCounts[10]={0,0,0,0,0,0,0,0,0,0};int max = a[0];for (int i = 1; i < len; i++) {if (a[i] > max) {max = a[i];}}do{maxLength++;max/=10;}while(max>0);for (int i = 0, n = 1; i < maxLength; i++, n*=10) {for (int j = 0; j < len; j++) {int digit = a[j] / n % 10;bucket[digit][eleCounts[digit]] = a[j];eleCounts[digit]++;}int index = 0;int eleCountsLength=sizeof(eleCounts)/sizeof(eleCounts[0]);for (int k = 0; k < eleCountsLength; k++) {if (eleCounts[k] != 0) {for (int l = 0; l < eleCounts[k]; l++) {a[index++] = bucket[k][l];}}eleCounts[k] = 0;}  }
}

结果如下：

 4、代码实现(包含负数)

#include <stdio.h>
int main(int argc, char *argv[])
{void radixSort(int a[],int len);int arr[]={20, -1, -18, 101, 319, 88};//得到数组的长度 int length=sizeof(arr)/sizeof(arr[0]);printf("基数(桶)排序前：");for (int i = 0; i < length; i++) {printf("%d ",arr[i]);}//因为有负数，所以先找到最小数(-18);int min = arr[0];for (int i = 0; i < length; i++) {if (min > arr[i]) {min = arr[i];}}//数组所有数据都减去该值for (int i = 0; i < length; i++) {arr[i] = arr[i] - min;}radixSort(arr,length);//按正整数排序，最后数组所有数据加上原最小数(-18)for (int i = 0; i < length; i++) {arr[i] = arr[i] + min;}printf("\n");printf("基数(桶)排序后：");for (int i = 0; i < length; i++) {printf("%d ",arr[i]);}printf("\n");return 0;
}
void radixSort(int a[],int len){//用二维数组来表示桶int bucket[10][len] ;//记录最大数的位数int maxLength=0;//用一维数组来表示桶中元素的个数//比如eleCounts[0]记录第0个桶中元素的个数int eleCounts[10]={0,0,0,0,0,0,0,0,0,0};int max = a[0];for (int i = 1; i < len; i++) {if (a[i] > max) {max = a[i];}}do{maxLength++;max/=10;}while(max>0);for (int i = 0, n = 1; i < maxLength; i++, n*=10) {for (int j = 0; j < len; j++) {int digit = a[j] / n % 10;bucket[digit][eleCounts[digit]] = a[j];eleCounts[digit]++;}int index = 0;int eleCountsLength=sizeof(eleCounts)/sizeof(eleCounts[0]);for (int k = 0; k < eleCountsLength; k++) {if (eleCounts[k] != 0) {for (int l = 0; l < eleCounts[k]; l++) {a[index++] = bucket[k][l];}}eleCounts[k] = 0;}  }
}

结果如下：

八：堆排序（heap sort）

 1、堆排序简要概述

  （1）堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。
  （2）堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆。
  （3）每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。
  （4）一般升序采用大顶堆，降序采用小顶堆
注意:没有要求结点的左孩子的值和右孩子的值的大小关系。

 2、大小顶堆图示

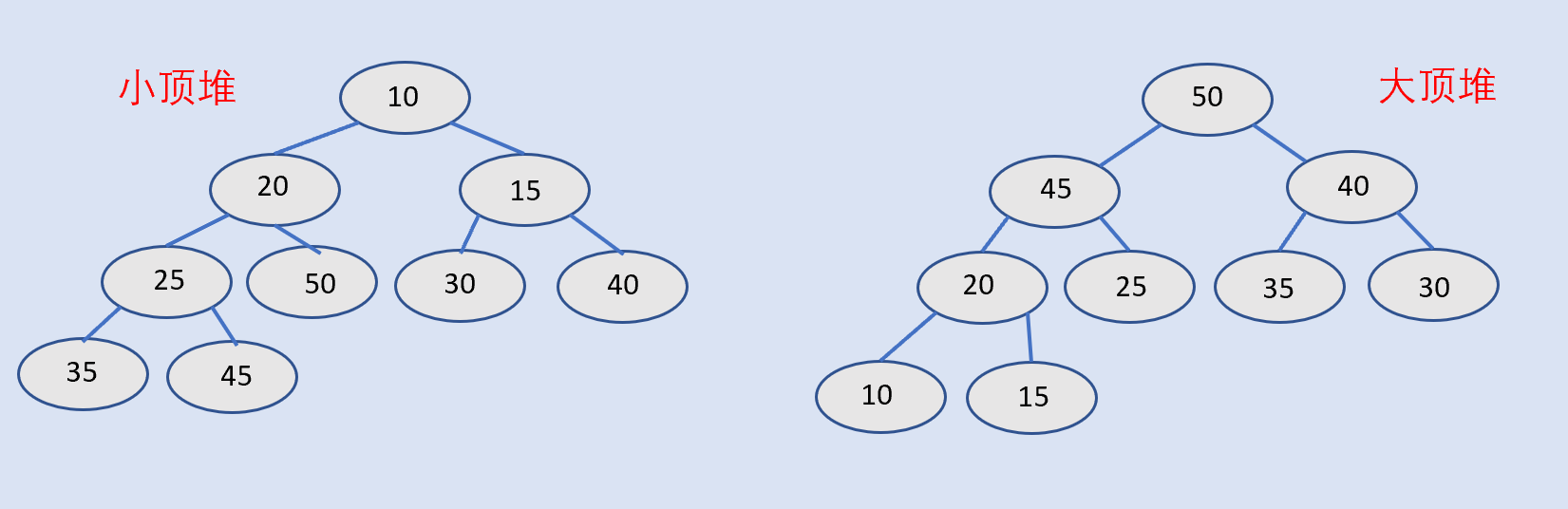
 3、堆排序基本思想

堆排序的基本思想是：
（1）将待排序序列构造成一个大顶堆
（2）此时，整个序列的最大值就是堆顶的根节点。
（3）将其与末尾元素进行交换，此时末尾就为最大值。
（4）然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了。

 4、代码实现

#include <stdio.h>
int main(int argc, char *argv[])
{void heapSort(int a[],int len);int arr[]={5, -1, -8, 10, 30, 20};//得到数组的长度 int length=sizeof(arr)/sizeof(arr[0]);printf("堆排序前：");for (int i = 0; i < length; i++) {printf("%d ",arr[i]);}heapSort(arr,length);printf("\n");printf("堆排序后：");for (int i = 0; i < length; i++) {printf("%d ",arr[i]);}printf("\n");return 0;
}
void heapSort(int a[],int len){void adjustHeap(int a[], int index, int length);int temp = a[len - 1];for (int i = len / 2 - 1; i >= 0; i--) {adjustHeap(a, i, len);}for (int j = len - 1; j > 0; j--) {temp = a[j];a[j] = a[0];a[0] = temp;adjustHeap(a, 0, j);}
}
void adjustHeap(int a[], int index, int length){int temp = a[index];for (int i = index * 2 + 1; i < length; i = i * 2 + 1) {if (i + 1 < length && a[i] < a[i + 1]) {i++;}if (a[i] > temp) {a[index] = a[i];index = i;} else {break;}}a[index] = temp;
}

结果如下：

---

楠哥-------一心想为IT行业添砖加瓦，却总是面向cv编程的程序员。
  谢谢阅读，无误点赞，有误还望评论区指正。

---