前缀和
前缀和是一种重要的预处理,能大大降低查询的时间复杂度。我们可以简单理解为“数列的前 n n n 项的和”。
例题
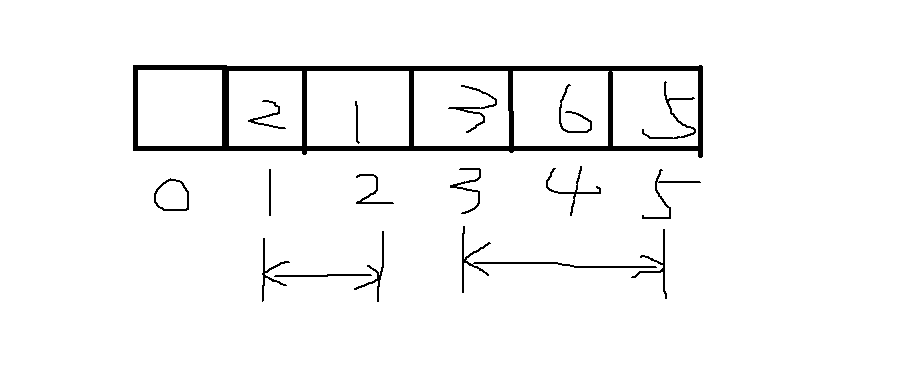
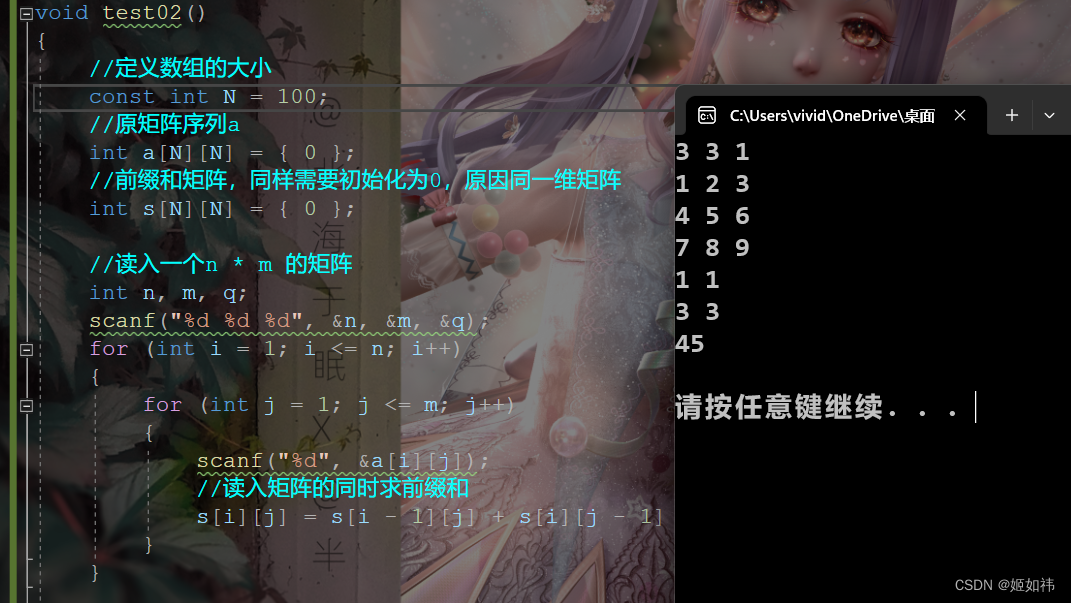
有 N N N 个的正整数放到数组 A A A 里,现在要求一个新的数组 B B B,新数组的第 i i i 个数 B [ i ] B[i] B[i]是原数组 A A A 第 0 0 0 到第 i i i 个数的和。
对于这道题,我们有两种做法:
- 把对数组 A A A 的累加依次放入数组 B B B 中。
- 递推: B [ i ] = B [ i − 1 ] + A [ i ] B[i] = B[i-1] + A[i] B[i]=B[i−1]+A[i] ,前提是 B [ 0 ] = A [ 0 ] B[0] = A[0] B[0]=A[0] 。
#include<bits/stdc++.h>
#define re register
#define f(i, a, b) for(re int i = a; i < b; i++)
using namespace std;int N; signed main(){scanf("%d", &N);int A[N + 1], B[N + 1];f(i, 0, N) scanf("%d", &A[i]);B[0] = A[0];f(i, 1, N) B[i] = B[i - 1] + A[i];f(i, 0, N) printf("%d ", B[i]);printf("\n");return 0;
}
二维/多维前缀和
其实前缀和几乎都是基于容斥原理
e g . eg. eg.有这样一个矩阵:
1 \boxed{1} 1 2 \boxed{2} 2 4 \boxed{4} 4 3 \boxed{3} 3
5 \boxed{5} 5 1 \boxed{1} 1 2 \boxed{2} 2 4 \boxed{4} 4
6 \boxed{6} 6 3 \boxed{3} 3 5 \boxed{5} 5 9 \boxed{9} 9
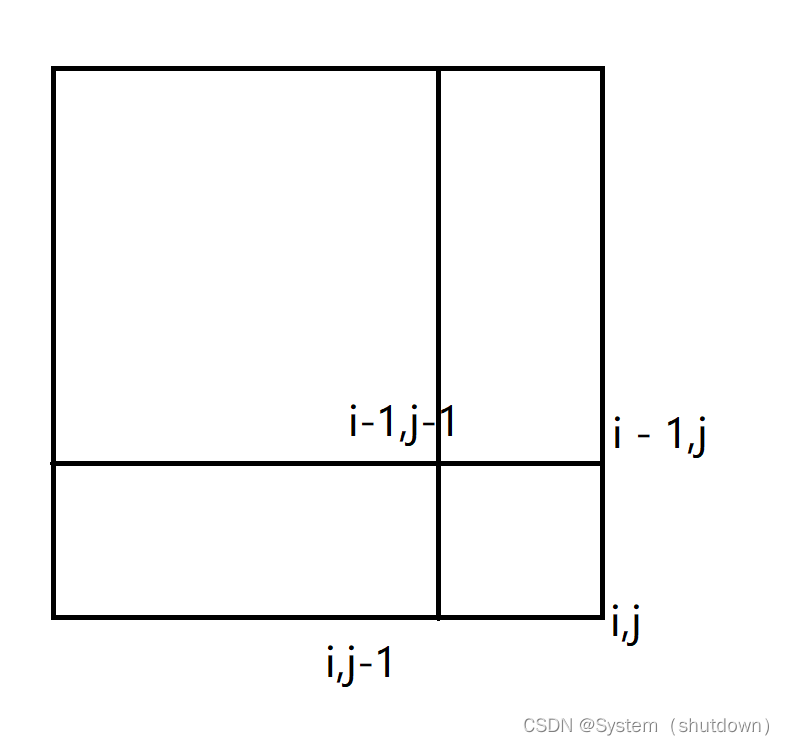
我们先定义个矩阵 s u m x , y = ∑ i = 1 x ∑ j = 1 y a i , j sum_{x,y}=\sum\limits_{i=1}^x\sum\limits_{j=1}^ya_{i, j} sumx,y=i=1∑xj=1∑yai,j
那么这个矩阵的前缀和就是:
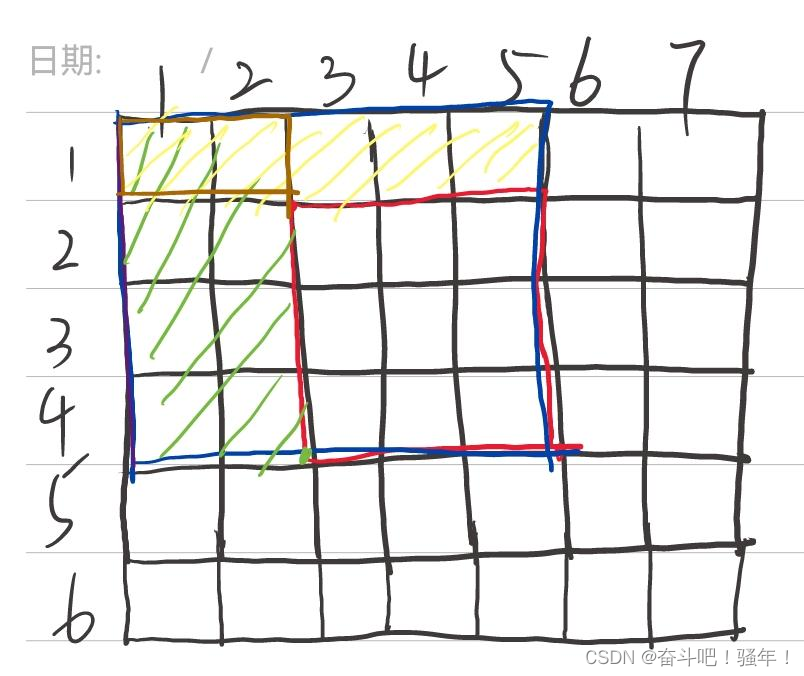
就拿 “ 15 ” “15” “15”来举例:
s u m 2 , 3 = s u m 1 , 3 + s u m 2 , 2 − s u m 1 , 2 + a 2 , 3 sum_{2,3}=sum_{1,3}+sum_{2,2}-sum_{1,2}+a_{2,3} sum2,3=sum1,3+sum2,2−sum1,2+a2,3
即 s u m 2 , 3 = 9 + 7 − 3 + 2 = 15 sum_{2,3}=9+7-3+2=15 sum2,3=9+7−3+2=15
⟹ s u m i , j = s u m i − 1 , j + s u m i , j − 1 − s u m i − 1 , j − 1 + a i , j \implies sum_{i,j}=sum_{i-1,j}+sum_{i,j-1}-sum_{i-1,j-1}+a_{i,j} ⟹sumi,j=sumi−1,j+sumi,j−1−sumi−1,j−1+ai,j
应用
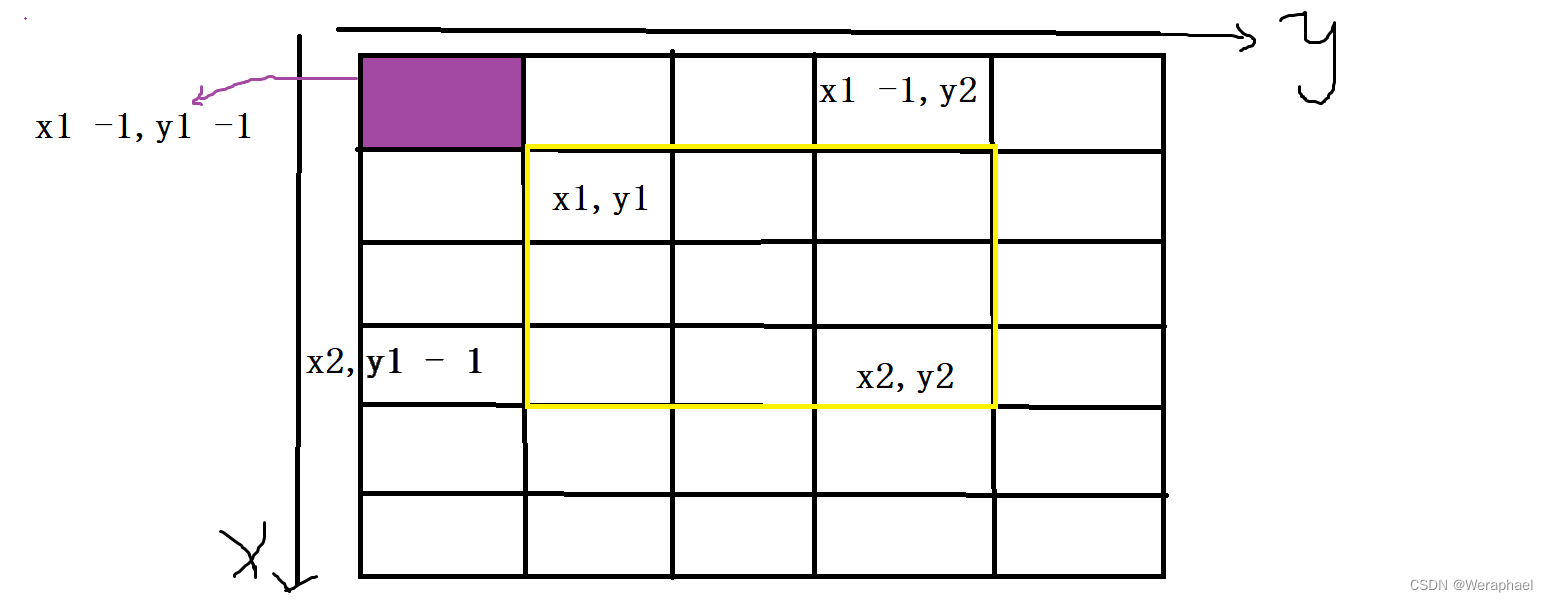
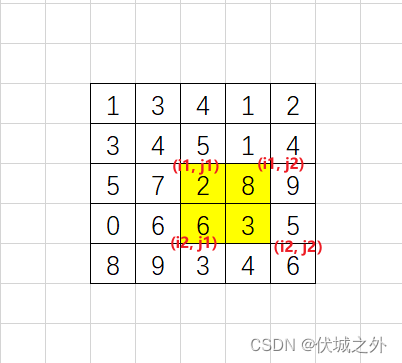
求 ( x 1 , y 1 ) − ( x 2 , y 2 ) (x_1,y_1)-(x_2,y_2) (x1,y1)−(x2,y2)子矩阵的和,类比以上的做法,易得: s u m x 2 , y 2 − s u m x 1 − 1 , y 2 − s u m x 2 , y 1 − 1 + s u m x 1 − 1 , y 1 − 1 \boxed{sum_{x_2,y_2}-sum_{x_1-1,y_2}-sum_{x_2,y_1-1}+sum_{x_1-1,y_1-1}} sumx2,y2−sumx1−1,y2−sumx2,y1−1+sumx1−1,y1−1
洛谷 P1387 最大正方形
题解