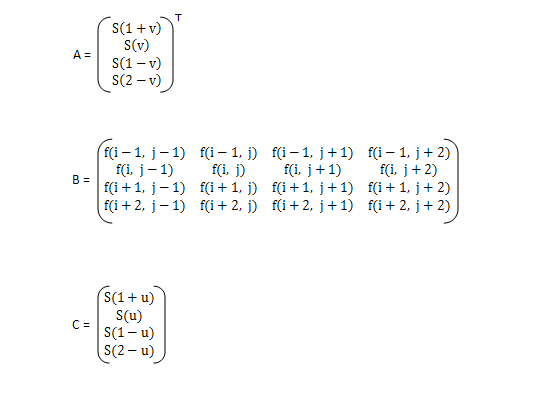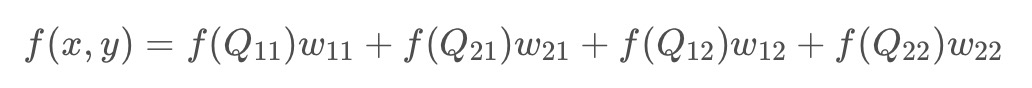插值算法是图像缩放中的一项基本且重要的算法；在图像缩放中，输出图像像素点坐标可能对应输入图像上几个像素点之间的位置，这个时候就需要通过灰度插值处理来计算出该输出点的灰度值。图像插值是图像超分辨率的重要环节，不同的插值算法有不同的进度，插值算法的好坏也直接影像着图像的失真程度。常用的插值算法有以下三种：最近邻插值算法、双线性插值算法以及双三次插值算法。

最近邻插值算法

最近邻插值算法是最简单的插值算法，同时也叫零阶插值法。即选择里它所映射位置最近的输入像素的灰度值为结果。对二维图像，是去待采样点周围4个相邻像素点中距离最近的1个点的灰度值作为待采样点的像素值。

最近邻插值算法 如上图所示，当需要求的A的坐标落在蓝色框内，会对其坐标（x,y）采用四舍五入的方式，将A点坐标映射到P1~P4上的某一个点，并以该点的灰度值作为采样点A的灰度值。

双线性插值算法

双线性插值素算法又叫一阶插值法，它对经过三次插值才能得到最终结果，是对最邻插值算法的一种改进，先对水平x方向进行一阶线性插值（需要两次一阶线性插值），然后在在垂直y方向进行一阶线性插值（只需要一次一阶线性插值）。

双线性插值算法

假设上图中，$Q_{11},Q_{12},Q_{21},Q_{22}$四个红色点的坐标点信息及灰度值是已知，分别为$Q_{11}=(x_1,y_1),Q_{12}=(x_1,y_2),Q_{21}=(x_2,y_1),Q_{22}=(x_2,y_2)$，通过双线性插值计算出P点的灰度值。
首先进行x方向的线性插值，得去$R_1,R_2$两点的灰度值，然后再进行y方向的线性插值，最终获取$P$点的灰度值。计算过程如下所示：
1. 计算x方向的线性插值
    $f(R1)=\frac{x_2-x}{x_2-x_1}f(Q_{11})+\frac{x-x_1}{x_2-x_1}f(Q_{21})Where{R}_1=(x,y_1)$

    $f(R2)=\frac{x_2-x}{x_2-x_1}f(Q_{12})+\frac{x-x_1}{x_2-x_1}f(Q_{22})Where{R}_1=(x,y_2)$

2.计算y方向的线性插值

    $f(P)=\frac{y_2-y}{y_2-y_1}f(R1)+\frac{y-y_1}{y_2-y_1}f(R2)$

3.合并1和2两步计算过程

    $f(P)=\frac{(x_2-x)(y_2-y)}{(x_2-x_1)(y_2-y_1)}f(Q_{11})+\frac{(x-x_1)(y_2-y)}{(x_2-x_1)((y_2-y_1))}(f(Q_{21}))+\frac{(x_2-x)(y-y_1)}{(x_2-x_1)(y_2-y_1)}f(Q_{12})+\frac{(x-x_1)(y-y_1)}{(x_2-x_1)(y_2-y_1)}f(Q_{22})$

双三次插值(bicubic)算法

双三次插值算法(Bicubic interpolation)又称立方卷积插值算法，是对双线性插值的改进，是一种比较复杂的插值方式，它不仅考虑到周围4个像素点灰度值的影像，还考虑到它们灰度值变化率的影像。该算法需要利用待采样附近16个像素点的灰度值作三次插值进行计算。

双三次插值(bicubic)算法

  如上图所示，函数$f$在点$(x,y)$的值可以通过矩形网络中最近的十六个采样点的甲醛平均得到的，在这里需要使用两个多项式三次插值函数，每个方向使用一个，其函数形式如下：
$$f(x,y)=\{\begin{array}{l}(a+2)|x{|}^3-(a+3)|x{|}^2+1for|x|<=1\\ a|x{|}^3-5a|x{|}^2+8a|x|-4afor1<|x|<=2\\ 0\end{array}$$
 说明：

• f(0)=1
• f(x)=0(当x>2)
• 当x超出范围的时候，f(x)为0
• 当a取不同值时，可以用来逼近不同的采样条函数（常用值为-0.5，0.75）

当$a=-1$时，如下：
$$f(x,y)=\{\begin{array}{l}|x{|}^3-2|x{|}^2+1for|x|<=1\\ -|x{|}^3+5|x{|}^2-8|x|+4for1<|x|<=2\\ 0\end{array}$$
此时，逼近的函数为$y=\frac{sin(x\ast PI)}{(x\ast PI)}$，如下所示：

当$a=-0.5$时，如下：
$$f(x,y)=\{\begin{array}{l}1.5|x{|}^3-2.5|x{|}^2+1for|x|<=1\\ -0.5|x{|}^3+2.5|x{|}^2-4|x|+2for1<|x|<=2\\ 0\end{array}$$
此时对应为三次Hermite样条，如下所示：

三种插值算法的优缺点

最近邻插值算法

	最近邻插值算法	双线性插值算法	双三次插值算法
采样方式	用距离采样点最近的像素值最为采样点的灰度值	用双线性方式计算采样点周围的4个点，计算其灰度值	根据采样点的周围16个像素值的双线性关系以及像素变化率，计算出采样点的灰度值
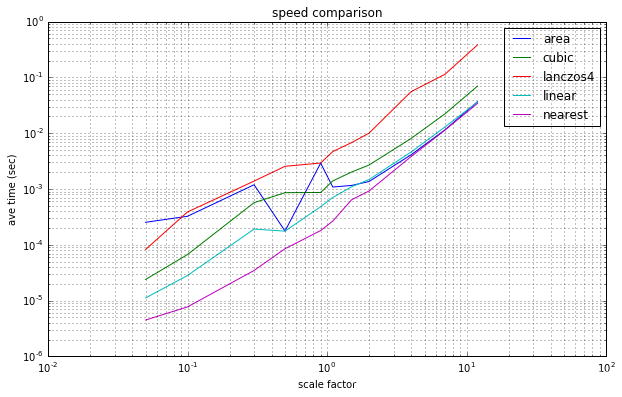
计算性能	计算量最小、最快	计算量比较大，速度居中	计算量最大，性能最慢
效果	未考虑周围像素点的影像，采样后的灰度值有明显的不连续性，图像质量损失较大，会产生马赛克或者锯齿现象	克服最近邻插值算法的灰度不连续性，未考虑各邻点的灰度值的相互影响，故具有低通滤波的性质，从而导致缩放后的图像的高频分量收到损失、图像边缘在一定程度上变得较为模糊	克服了前两种方法的不足之处，能够产生比双线性茶壶中算法更为平滑的边缘，计算精度很高，处理后的图像质量损失最少，效果最佳的

注：在进行图像缩放时应根据实际情况对三种算法做出选择，既要考虑时间方面的可行性，也要考虑对变化后图像质量可用性，这样才能达到较为理想结果。