插值算法

一、算法介绍

（一）算法引入

对于数据量少到不足以去分析问题，而必须生成一些合理的数据的情况要用到插值算法。

（二）算法详解

（1）定义
设函数 $y = f (x)$ 在区间 $[a, b]$ 上有定义，且已知在点 $a≤x_0<x_1<...<x_n≤b$ 上的值分别为： $y_0,y_1...y_n$ ，若存在一简单函数 $P (x)$ ，使得
$P(x_i)=y_i,i∈N$
则称 $P (x)$ 为 $f (x)$ 的插值函数。
称 $x_0,x_1...x_n$ 为插值节点。
称 $[a, b]$ 为插值区间。
称求插值函数 $P (x)$ 的方法为插值法。

总结信息：找到一个能完美通过所有数据点的函数（特别强调：简单是指次数尽可能低）。

（2）两种实用插值算法

分段三次Hermite插值

条件：

在节点上的函数值相等。
对应的导数值相等。
高阶导数值也相等。

说明：对于普通的Hermite算法插值所生成的多项式次数高，容易产生龙格现象（Runge phenomenon）。因此需要分成三次使用Hermite算法，生成三段函数，叫做分段三次Hermite插值多项式（PCHIP）。原理复杂无需了解。

三次样条插值

条件：

在节点上的函数值相等。
在每个子区间上函数是三次多项式。
函数在区间上二阶连续可微。

说明：在某些情况下三次样条插值比三次分段Hermite插值算法所生成的插值函数更加光滑，但有时不一定，因此尽量两种方法都试一试。

（三）算法举例

利用插值算法预测短期（4年之内）人口数量变化情况。
（1）数据

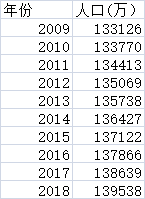
将准备好的数据导入设定的两个向量year,population中.

（2）执行算法

分段三次Hermite插值

%设x是已知样本点横坐标，y是已知样本点纵坐标，new_x是要插入处对应的横坐标。
p=pchip(x,y,new_x)
%因此本题生成函数应写成
p1=pchip(year,population,2019:2022);

三次样条插值

%同上段程序题设
p=spline(x,y,new_x)
p2=spline(year,population,2019:2022);

（3）预测绘图

%通过绘图比较两种插值算法对应效果
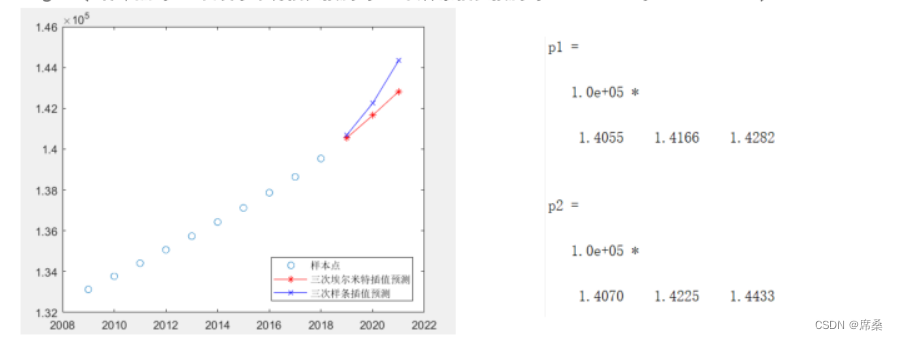
plot(x,y,'o',new_x,p1,'r-',new_x,p2,'b-');
legend('样本点','分段三次Hermite插值','三次样条插值','Location','SouthEast');

红色为三次分段Hermite插值生成函数，蓝色为三次样条插值算法生成函数。

说明：只是拿短期人口预测做插值举例，真正建模中要做人口预测用拟合算法或者之后专门预测模型更好！

二、算法实现

分段三次Hermite插值算法

p=pchip(x,y,new_x);
plot(x,y,'o',new_x,p,'r-');

三次样条插值算法

p=spline(x,y,new_x);
plot(x,y,'o',new_x,p,'r-');

三、算法应用

（一）题目描述

某水池中在奇数周的水池各项指标如下表所示，其中一行代表一项指标，请补充偶数周该水池各项指标值。

（二）算法实战

（1）插值算法生成数据

%考虑三次分段Hermite插值函数pchip(x,y,new_x)。
%x为已知数据点对应的自变量值。
%y为已知数据点的因变量值。
%new_x为待插值数据点所对应的自变量值。
%假设将该水池所对应的数据已导入Z.mat中。
load Z.mat
x=Z(1,:);
[n,m]=size(Z);
P=zeros(11,15);
for i=2:ny=Z(i,:);new_x=1:15;p1=pchip(x,y,new_x);subplot(4,3,i-1);P(i-1,:)=p1;     
end
P = [1:15; P]

导入已知数据点的自变量x。
导入已知数据点的因变量y。
导入待插入数据点的自变量new_x。

（2）绘制图形

引自别人绘图代码

（三）总结思考

1、算法对比与评价：可以使用三种插值算法分别进行插值。lagrange插值、三次分段Hermite插值与三次样条插值。
（1）lagrange插值算法：总体来看，插值数据能近似反映缺失值的真实情况，但是该算法不具有继承性，且所生成的函数存在Runge现象，个别插值数据明显脱离实际，XXX数据值为负数，这显然不合实际，说明拉格朗日插值法存在局限性。
（2）三次分段Hermite插值算法：插值数据具有更高的精度，但在插值节点处是不光滑不准确的。
（3）三次样条插值算法：当插值节点的密度逐渐变大时，三次样条插值函数不但收敛于函数本身及其微商，也收敛于函数的微商，因此这一特性使得该算法具有更高的插值精度。

2、算法功能：该插值算法在整个数学建模竞赛中只能起到数据预处理的作用，根本不在建模过程中，因此论文写作若用到该算法要另开标题。