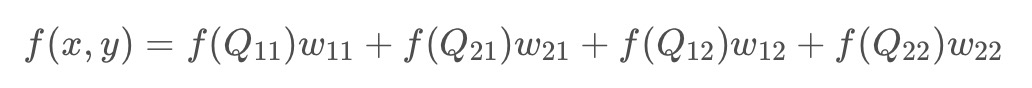插值算法总结

1、最邻近元法

　　这是最简单的一种插值方法，不需要计算，在待求象素的四邻象素中，将距离待求象素最近的邻象素灰度赋给待求象素。设i+u, j+v(i, j为正整数， u, v为大于零小于1的小数，下同)为待求象素坐标，则待求象素灰度的值 f(i+u, j+v)　如下图所示：

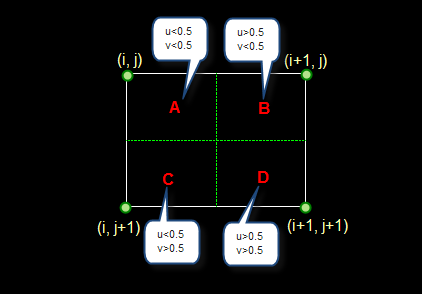
如果(i+u, j+v)落在A区，即u<0.5, v<0.5，则将左上角象素的灰度值赋给待求象素，同理，落在B区则赋予右上角的象素灰度值，落在C区则赋予左下角象素的灰度值，落在D区则赋予右下角象素的灰度值。

最邻近元法计算量较小，但可能会造成插值生成的图像灰度上的不连续，在灰度变化的地方可能出现明显的锯齿状。

2、双线性内插法

双线性内插法是利用待求象素四个邻象素的灰度在两个方向上作线性内插，如下图所示：

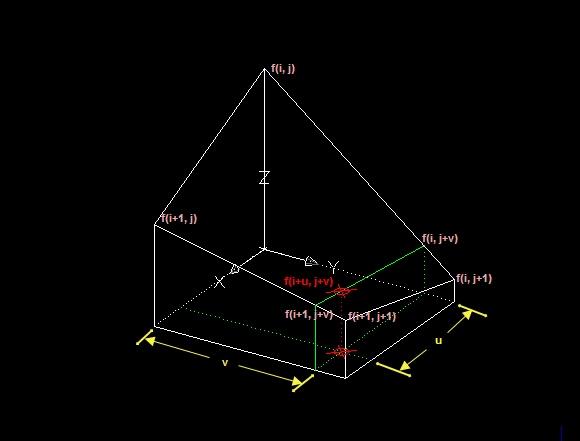
对于 (i, j+v)，f(i, j) 到 f(i, j+1) 的灰度变化为线性关系，则有：

　　　　　　f(i, j+v) = [f(i, j+1) - f(i, j)] * v + f(i, j)

同理对于 (i+1, j+v) 则有：

f(i+1, j+v) = [f(i+1, j+1) - f(i+1, j)] * v + f(i+1, j)

从f(i, j+v) 到 f(i+1, j+v) 的灰度变化也为线性关系，由此可推导出待求象素灰度的计算式如下：

f(i+u, j+v) = (1-u) * (1-v) * f(i, j) + (1-u) * v * f(i, j+1) + u * (1-v) * f(i+1, j) + u * v * f(i+1, j+1)

双线性内插法的计算比最邻近点法复杂，计算量较大，但没有灰度不连续的缺点，结果基本令人满意。它具有低通滤波性质，使高频分量受损，图像轮廓可能会有一点模糊。

3、三次内插法

该方法利用三次多项式S(x)求逼近理论上最佳插值函数sin(x)/x, 其数学表达式为：

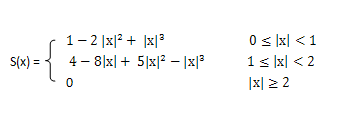
待求像素(x, y)的灰度值由其周围16个灰度值加权内插得到，如下图：

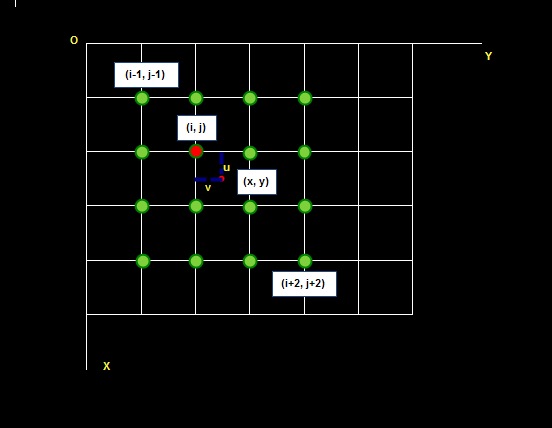
待求像素的灰度计算式如下：

f(x, y) = f(i+u, j+v) = ABC

其中:

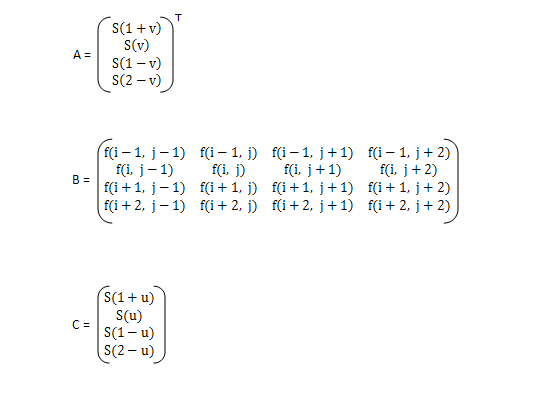
三次曲线插值方法计算量较大，但插值后的图像效果最好。

插值方法总结：

“Inverse Distance to a Power（反距离加权插值法）”、
“Kriging（克里金插值法）”、
“Minimum Curvature（最小曲率)”、
“Modified Shepard's Method（改进谢别德法）”、
“Natural Neighbor（自然邻点插值法）”、
“Nearest Neighbor（最近邻点插值法）”、
“Polynomial Regression（多元回归法）”、
“Radial Basis Function（径向基函数法）”、
“Triangulation with Linear Interpolation（线性插值三角网法）”、
“Moving Average（移动平均法）”、
“Local Polynomial（局部多项式法）”

1、距离倒数乘方法
距离倒数乘方格网化方法是一个加权平均插值法，可以进行确切的或者圆滑的方式插值。方次参数控制着权系数如何随着离开一个格网结点距离的增加而下降。对于一个较大的方次，较近的数据点被给定一个较高的权重份额，对于一个较小的方次，权重比较均匀地分配给各数据点。
计算一个格网结点时给予一个特定数据点的权值与指定方次的从结点到观测点的该结点被赋予距离倒数成比例。当计算一个格网结点时，配给的权重是一个分数，所有权重的总和等于1.0。当一个观测点与一个格网结点重合时，该观测点被给予一个实际为 1.0 的权重，所有其它观测点被给予一个几乎为 0.0 的权重。换言之，该结点被赋给与观测点一致的值。这就是一个准确插值。
距离倒数法的特征之一是要在格网区域内产生围绕观测点位置的"牛眼"。用距离倒数格网化时可以指定一个圆滑参数。大于零的圆滑参数保证，对于一个特定的结点，没有哪个观测点被赋予全部的权值，即使观测点与该结点重合也是如此。圆滑参数通过修匀已被插值的格网来降低"牛眼"影响。

2、克里金法
克里金法是一种在许多领域都很有用的地质统计格网化方法。克里金法试图那样表示隐含在你的数据中的趋势，例如，高点会是沿一个脊连接，而不是被牛眼形等值线所孤立。
克里金法中包含了几个因子：变化图模型，漂移类型和矿块效应。

3、最小曲率法
最小曲率法广泛用于地球科学。用最小曲率法生成的插值面类似于一个通过各个数据值的，具有最小弯曲量的长条形薄弹性片。最小曲率法，试图在尽可能严格地尊重数据的同时，生成尽可能圆滑的曲面。
使用最小曲率法时要涉及到两个参数：最大残差参数和最大循环次数参数来控制最小曲率的收敛标准。

4、多元回归法
多元回归被用来确定你的数据的大规模的趋势和图案。你可以用几个选项来确定你需要的趋势面类型。多元回归实际上不是插值器，因为它并不试图预测未知的 Z 值。它实际上是一个趋势面分析作图程序。
使用多元回归法时要涉及到曲面定义和指定XY的最高方次设置，曲面定义是选择采用的数据的多项式类型，这些类型分别是简单平面、双线性鞍、二次曲面、三次曲面和用户定义的多项式。参数设置是指定多项式方程中 X 和 Y组元的最高方次。

5、径向基本函数法
径向基本函数法是多个数据插值方法的组合。根据适应你的数据和生成一个圆滑曲面的能力，其中的复二次函数被许多人认为是最好的方法。所有径向基本函数法都是准确的插值器，它们都要为尊重你的数据而努力。为了试图生成一个更圆滑的曲面，对所有这些方法你都可以引入一个圆滑系数。你可以指定的函数类似于克里金中的变化图。当对一个格网结点插值时，这些个函数给数据点规定了一套最佳权重。

6、谢别德法
谢别德法使用距离倒数加权的最小二乘方的方法。因此，它与距离倒数乘方插值器相似，但它利用了局部最小二乘方来消除或减少所生成等值线的"牛眼"外观。谢别德法可以是一个准确或圆滑插值器。
在用谢别德法作为格网化方法时要涉及到圆滑参数的设置。圆滑参数是使谢别德法能够象一个圆滑插值器那样工作。当你增加圆滑参数的值时，圆滑的效果越好。

7、三角网/线形插值法
三角网插值器是一种严密的插值器，它的工作路线与手工绘制等值线相近。这种方法是通过在数据点之间连线以建立起若干个三角形来工作的。原始数据点的连结方法是这样：所有三角形的边都不能与另外的三角形相交。其结果构成了一张覆盖格网范围的，由三角形拼接起来的网。
每一个三角形定义了一个覆盖该三角形内格网结点的面。三角形的倾斜和标高由定义这个三角形的三个原始数据点确定。给定三角形内的全部结点都要受到该三角形的表面的限制。因为原始数据点被用来定义各个三角形，所以你的数据是很受到尊重的。

8.自然邻点插值法
自然邻点插值法(NaturalNeighbor)是Surfer7.0才有的网格化新方法。自然邻点插值法广泛应用于一些研究领域中。其基本原理是对于一组泰森(Thiessen)多边形,当在数据集中加入一个新的数据点(目标)时,就会修改这些泰森多边形,而使用邻点的权重平均值将决定待插点的权重, 待插点的权重和目标泰森多边形成比例。实际上,在这些多边形中,有一些多边形的尺寸将缩小,并且没有一个多边形的大小会增加。同时,自然邻点插值法在数据点凸起的位置并不外推等值线(如泰森多边形的轮廓线)。

9.最近邻点插值法
最近邻点插值法(NearestNeighbor)又称泰森多边形方法,泰森多边形(Thiesen,又叫Dirichlet或Voronoi多边形)分析法是荷兰气象学家A.H.Thiessen提出的一种分析方法。最初用于从离散分布气象站的降雨量数据中计算平均降雨量,现在GIS和地理分析中经常采用泰森多边形进行快速的赋值。实际上,最近邻点插值的一个隐含的假设条件是任一网格点p(x,y)的属性值都使用距它最近的位置点的属性值,用每一个网格节点的最邻点值作为待的节点值。当数据已经是均匀间隔分布,要先将数据转换为SURFER的网格文件,可以应用最近邻点插值法;或者在一个文件中,数据紧密完整,只有少数点没有取值,可用最近邻点插值法来填充无值的数据点。有时需要排除网格文件中的无值数据的区域,在搜索椭圆 (SearchEllipse)设置一个值,对无数据区域赋予该网格文件里的空白值。设置的搜索半径的大小要小于该网格文件数据值之间的距离,所有的无数据网格节点都被赋予空白值。在使用最近邻点插值网格化法,将一个规则间隔的XYZ数据转换为一个网格文件时,可设置网格间隔和XYZ数据的数据点之间的间距相等。最近邻点插值网格化法没有选项,它是均质且无变化的,对均匀间隔的数据进行插值很有用,同时,它对填充无值数据的区域很有效。