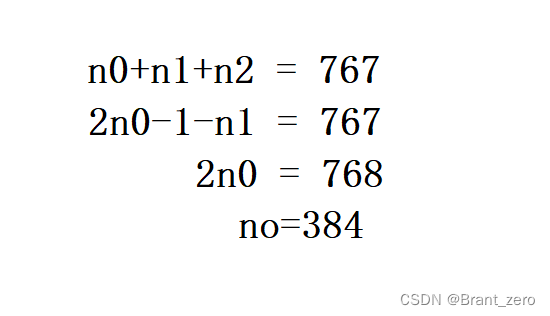1、前言
在现实生活中,大部分事物之间的关系都是非常复杂的,单从事物联系的数量来说,有的是一对一的关系,有的是一对多的关系,有的是多对多的关系。这就诞生了除了线性结构以外,还包含了树结构和图结构。树结构通常来免回一对多的关系,图结构则总是用在多对多的关系。前者比如族谱,后者比如交通图。因此,对于它们的了解,可以加强我们对现实生活的事物之间的抽象理解,这样才可以开发处符合现实生活的数据结构。本文主要讲解树结构 。
2、树结构的概念
接下来通过二叉树来了解树结构,因为二叉树是一个典型的例子,通过它就可以推广到整个树结构。
二叉树是有限个数据元素的集合,这个集合或者为空,或者只有一个根节点,又或者含有左子树和右子树的二叉树。当集合为空时,则称为这个二叉树为空二叉树。二叉树的每一个元素又称为节点。
3、树结构相关专业术语
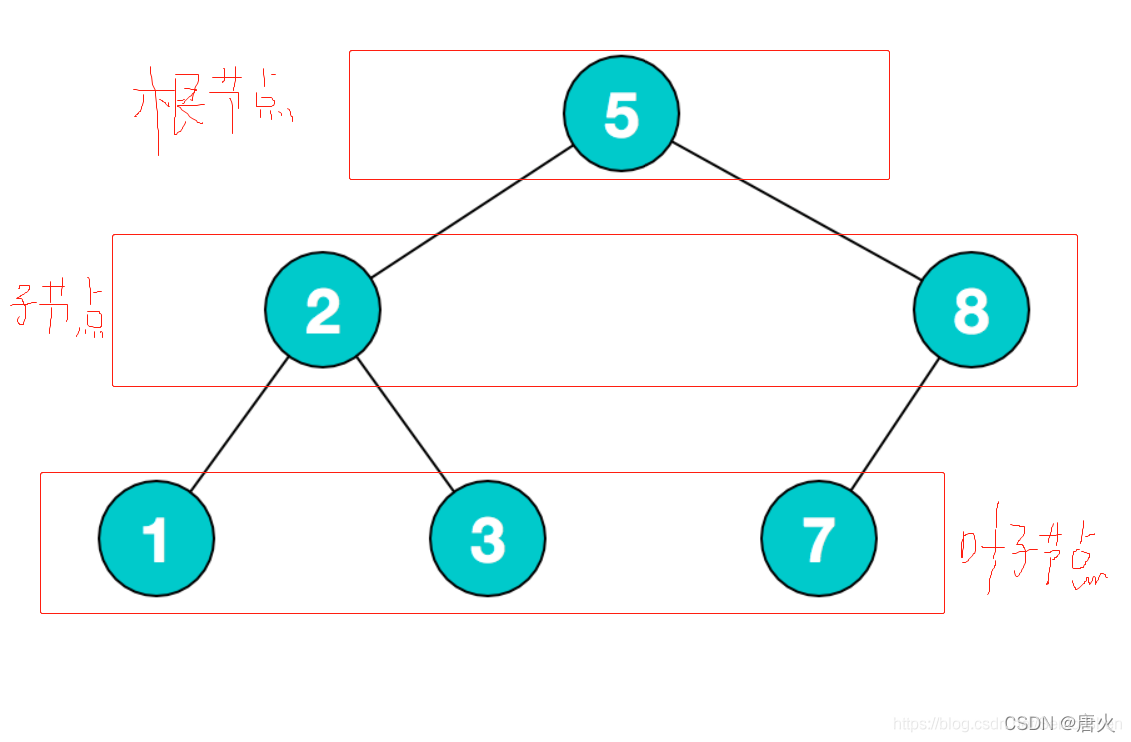
节点的度:节点的分支数叫做这个节点的度。
叶节点:节点的分支数为0的节点称为叶节点。既不含有子元素。
分支节点:节点的分支数不为0的节点称为分支节点。即含有子元素。
左孩子,右孩子,双亲,兄弟:如果一个节点拥有子元素,那么它的左边的子元素称为左孩子,右边的子元素称为右孩子。对于孩子节点来说,这个节点就是双亲节点。而左孩子与右孩子互相又称为兄弟节点。
路径,路径长度:如果一棵树中的含有一串节点,节点n 1,n2......nk,其中ni是ni-1的父元素,则称这段节点为n1到nk的路径。这段路径的长度为k-1。
祖先,子孙:如果存在一条从ni到nk的路径,则称ni是nk的在子孙。
节点的层数:规定根节点的层数为1,其余节点为其父节点的层数+1。
满二叉树:如果一棵树的每一层的节点都达到了最大值(2的(n-1)次方),则称这棵树为满二叉树。满二叉树的特点除了叶子结点外,所有的分支节点都含有左子树和右子树。
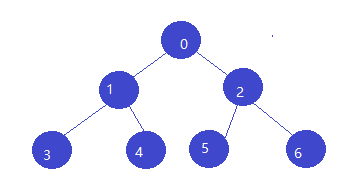
完全二叉树:假设根节点的标号是1,其余节点均按次序从上到下,从左到右编号,每个编号均和满二叉树相同,则称这棵二叉树为完全二叉树。完全二叉树不一定是满二叉树,满二叉树一定是完全二叉树。因为完全二叉树的最后一层的节点可以不达到该层的最大节点数。
4、二叉树的主要性质以及证明
性质1 一棵非空二叉树第i层上最多有2的(i-1)次方个节点(i>=1)
思路:这种证明题,通常都是使用数学归纳法证明的。
证明:

性质2:一棵深度额为k的二叉树,最多具有2的k次方-1个节点。
证明思路:证明每一层的节点数相加不超过2的k次方-1即可。
证明: 

性质3:对于一颗非空的二叉树,若叶子结点数为n0,度数为2的节点数为n2,则有n0=n2+1
证明思路:要证明度数为0的节点和度数为2的节点的关系,我们需要为他们之间建立关系式。首先可以从节点总数出发,即n=n0+n1+n2,接着我们需要借助其他证明把n1和n0以及n2的关系求出来,既可以得到n0和n2的关系。
证明:

性质4:由于涉及到对数,不好写直接上图。

5、二叉树的基本运算
1、initial,建立一棵空的二叉树。建议的做法是用一个头节点指向根节点。
2、create,创建二叉树的根节点。
3、insertL,给根节点插入左孩子节点,如果根节点本身含有左孩子节点,则将原来的左孩子节点作为当前结点的左孩子节点,当前结点则作为根节点的左孩子节点。
4、insertR,给根结点插入右孩子节点,如果根节点本身含有右孩子节点,则将原来的右孩子节点作为当前结点的右孩子节点,当前结点则作为根节点的右孩子节点。
5、deleteL,在二叉树中删除某个节点的左子树。
6、deleteR,在二叉树中删除某个节点的右子树。
7、search,在二叉树中查找某个值得节点元素。
8、traverse,遍历二叉树的所有节点。常用的遍历方式有三种,前序遍历,中序遍历,后序遍历。后面会展开讲解。
6、二叉树的存储方式
基本运算是数据结构的逻辑实现,具体的实现必须确认了存储方式才能实现,所以现在必须先了解二叉树可用的存储方式。
6.1、顺序存储结构
顺序存储结构在实现上就是利用数组来存储一组相邻的元素。在二叉树中,分为满二叉树,完全二叉树以及一般的二叉树。事实上,如果用数组来存储二叉树的元素,这里按照从上到下,从左到右的次序存储二叉树中的元素。考虑到相邻元素之间必须在二叉树里面也是相邻的,也只有满二叉树,完全二叉树可以毫无缝隙的对接树的相邻元素和数组的相邻元素恰好是相邻关系。而一般的二叉树,如果也希望用数组存储,并且数组的相邻元素在二叉树上也是相邻元素,只能对树结构进行完全化后再进行存储。
完全化:即对于树中的元素,按照从上到下,从左到右的次序存储,一旦遇到空的元素,就用NULL补齐,直到最后一个元素被存储。这样,如果相邻的元素是NULL,说明该元素并没有在树结构上相邻的元素。因为看上去用NULL补齐的树,就像一棵完全二叉树,所以称为完全化。
综上所述,如果二叉树的结构是满二叉树或者完全二叉树,那么可以考虑使用数组存储。但如果是一般的二叉树则不建议,因为完全化后的二叉树,空元素也需要占据空间,但实际上,这些元素并没有实际含义,所以会导致大量的空间浪费。
无论什么结构的二叉树,都建议使用链式存储结构。
6.2、链式存储结构
链式存储结构,即用链表的方式存储二叉树的结构,在此又分为二叉链表存储和三叉链表存储,它们的结构如下:
二叉链表:

三叉链表:
二叉链表存储,包含三个信息,左孩子节点指针,右孩子节点指针,以及数据域。如果没有孩子节点,则将指针域置为NULL。使用二叉链表结构,一般会创建一个头节点,并将其中的左子树指向根节点,右子树为NULL,这样方便了后续的操作。
三叉链表存储,除了含有二叉链表的结构外,还含有一个双亲节点指针域,指向它的双亲节点。这是典型的空间换时间的方法,如果涉及的操作需要频繁访问双亲节点,就建议使用三叉链表的存储结构。
对于一般的二叉树而言,二叉链表存储是最简单有效的方式,也是推荐使用的。
7、二叉链表的基本实现
在给出代码之前,先讲述二叉树的遍历方法。
先序遍历是先访问父元素在访问左孩子最后是右孩子。
中序遍历是先访问左孩子再访问父节点最后是右孩子。
后序遍历是先访问左孩子在访问右孩子最后访问父节点。
看了很多解释遍历的解说,都是特别抽象难懂的,笔者的建议是,结合代码以及提到的遍历的方法,一步一步调试,才会比较容易的去理解。
代码如下:
Node.h
#include<string>class Node
{
public:Node();~Node();std::string data;Node *lChild;Node *rChild;private:};Node::Node()
{
}Node::~Node()
{
}BinaryTree.h
#include "Node.h"
#include <iostream>
#include<stack>/*
初始化二叉树的表头
*/
Node *initial()
{Node *header = new Node;header->lChild = nullptr;header->rChild = nullptr;header->data = " ";return header;
}/*
创建根节点
*/
void createRoot(std::string data, Node *header)
{Node *root = new Node();root->data = data;root->lChild = nullptr;root->rChild = nullptr;header->lChild = root;//将树的根节点保存在头节点的左节点。以后的操作只要正对根节点就行了
}/*
给根结点添加左孩子节点,如果根节点本身就存在左孩子节点就将当前结点作为根节点的左孩子,之前的左孩子节点作为新的节点的左孩子节点
*/void insertL(std::string data, Node *header)
{Node *root = header->lChild;Node *lChild = new Node();lChild->data = data;lChild->rChild = nullptr;//新添加的节点应该是不含孩子节点的,但如果根节点本身就有左孩子节点,则此节点有左孩子节点if (root->lChild != nullptr)lChild->lChild = root->lChild;elselChild->lChild = nullptr;root->lChild = lChild;
}/*
给根结点添加右孩子节点,如果根节点本身就存在右孩子节点就将当前结点作为根节点的右孩子,之前的右孩子节点作为新的节点的右孩子节点
*/void insertR(std::string data, Node *header)
{Node *root = header->lChild;Node *rChild = new Node();rChild->data = data;rChild->lChild = nullptr;//新添加的节点应该是不含孩子节点的,但如果根节点本身就有右孩子节点,则此节点有右孩子节点if (root->rChild != nullptr)rChild->rChild = root->rChild;elserChild->rChild = nullptr;root->rChild = rChild;
}/*
删除某个节点的左子树
*/
void deleteL(Node *parent, Node *header)
{if (parent == nullptr || parent->lChild == nullptr)return;else{Node *lChild = parent->lChild;parent->lChild = nullptr;lChild = nullptr;free(lChild);}
}/*
删除某个节点的右孩子树
*/
void deleteR(Node *parent, Node *header)
{if (parent == nullptr || parent->rChild == nullptr)return;else{Node *rChild = parent->rChild;parent->rChild = nullptr;rChild = nullptr;free(rChild);}
}/*
查找某个数据的节点元素
*/Node *search(std::string data, Node *header)
{Node *root = header->lChild;Node *item = header->lChild;std::stack<Node *> nodeStack;nodeStack.push(item);//先序遍历查找节点 while (item != nullptr || nodeStack.size() != 0){while (item != nullptr){if (item->data == data)return item;if (item != header->lChild)nodeStack.push(item);item = item->lChild;}if (nodeStack.size() == 0)return nullptr;item = nodeStack.top();nodeStack.pop();item = item->rChild;}return nullptr;}/*
先序遍历二叉树
*/
void preTraveler(Node *header)
{Node *item = header->lChild;//需要用一个栈来保存所有访问过的元素,这样才能访问当前元素的父元素std::stack<Node *> nodeStack;nodeStack.push(item);//只有当栈没有元素了,item也是null的时候,才说明二叉树访问完毕while (item != nullptr || nodeStack.size() != 0){while (item != nullptr){//将左子树入栈std::cout << item->data << " ";if (item != header->lChild)nodeStack.push(item);item = item->lChild;}//如果栈中没有元素,说明所有的元素都访问过了。if (nodeStack.size() == 0)return;//弹出栈顶元素item = nodeStack.top();nodeStack.pop();item = item->rChild;}}/*
中序遍历二叉树
和先序遍历不同的地方在于,访问节点数据的位置不同。
先序遍历是先访问节点在入栈,中序遍历则是先入栈在访问节点
*/
void midTraveler(Node *header)
{Node *item = header->lChild;std::stack<Node *> nodeStack;nodeStack.push(item);while (item != nullptr || nodeStack.size() != 0){while (item != nullptr){if (item != header->lChild)nodeStack.push(item);item = item->lChild;}if (nodeStack.size() == 0)return;item = nodeStack.top();std::cout << item->data << " ";nodeStack.pop();item = item->rChild;}}#include"BinaryTree.h"
#include<sstream>//fstreamint main()
{Node *header = initial();createRoot("root", header);//创建根节点//将偶数插入左子树,奇数插入右子树。//由于每次都插入到根节点的字数,导致数的结构是左子树只有左孩子,右子树只有右孩子。//其实insertL可以传递的header可以改成需要作为父元素的节点,这样就可避免除出现签名的情况std::stringstream inS;for (int i = 1; i <= 100; i++){inS <<std::unitbuf<< i<<std::nounitbuf;if (i % 2 == 0)insertL(inS.str(), header);elseinsertR(inS.str(), header);inS.str("");//必须情况内容,否则的话,会把前面的内容拼合起来}//先序遍历preTraveler(header);std::cout << std::endl;//中序遍历midTraveler(header);return 0;
}笔者只是实现了先序遍历和中序遍历,后续遍历的流程比较复杂一点,目前暂时没有思路。有兴趣的读者可以自己去研究。
---------文章写自:HyHarden---------
--------博客地址:http://blog.csdn.net/qq_25722767-----------