树的基本概念

基本概念

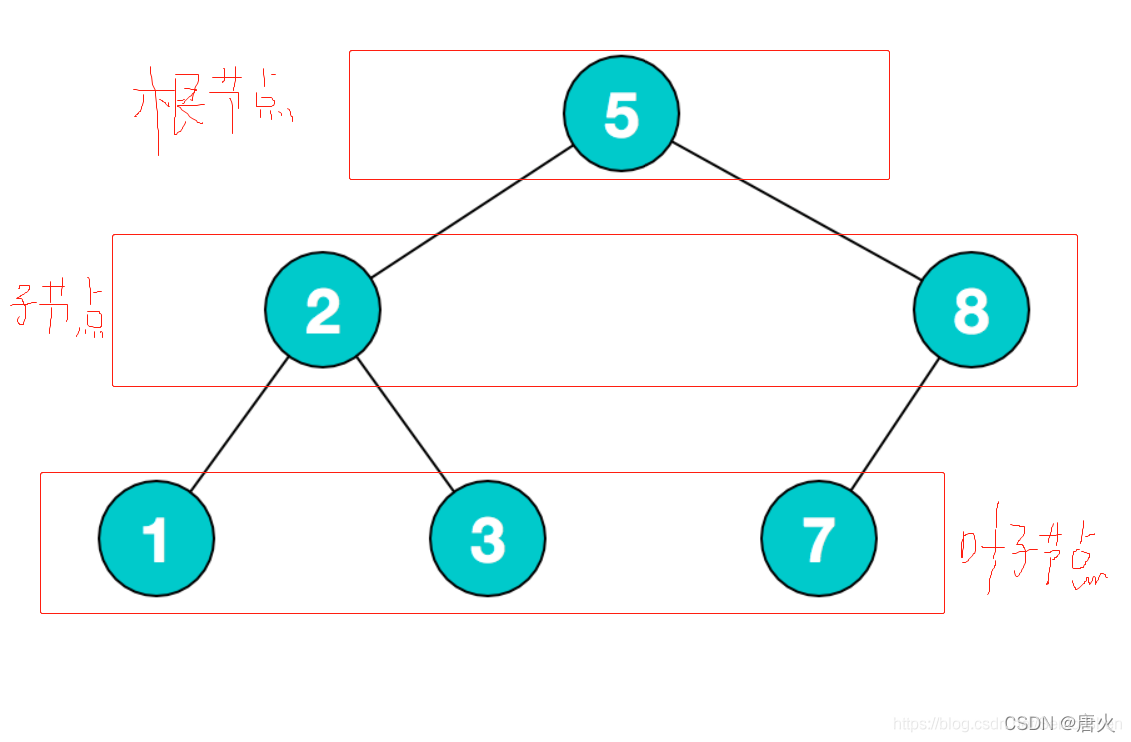
树的度—— 一棵树中最大的结点度数
双亲—— 孩子结点的上层结点叫该结点的双亲
兄弟—— 同一双亲的孩子之间互成为兄弟
祖先—— 结点的祖先是从根到该结点所经分支上的所有结点
子孙—— 以某结点为根的子树中的任一结点都成为该结点的子孙
结点的层次—— 从根结点算起，根为第一层，它的孩子为第二层……
堂兄弟—— 其双亲在同一层的结点互称为堂兄弟。
深度—— 树中结点的最大层次数
有序树—— 如果将树中结点的各子树看成从左至右是有次序的（即不能互换），则称该树为有序树，否则称为无序树。在有序树中最左边的子树的根称为第一个孩子，最右边的称为最后一个孩子。
森林—— m(m0)棵互不相交的树的集合

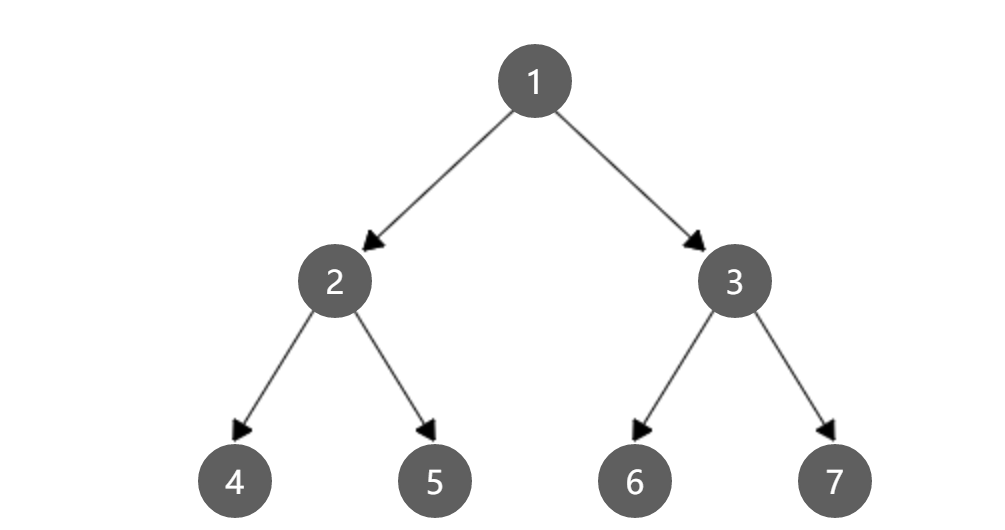
形象表示

m叉树定义

每个结点的度数 <= m;

二叉树

于是二叉树有如下五种形态

二叉树的子树有左右之分，不能颠倒

特殊的二叉树

满二叉树

重点是满
形象表示（图片中数字仅代表编号，不代表真实数值）

1.定义： 高度为h，并且含有(2^h)-1个结点的二叉树
2.对于编号为 i 的结点，如果有双亲，双亲为 i/2 向下取整；如果有左孩子，左孩子编号为 2i，如果有右孩子，右孩子编号为 (2i + 1)

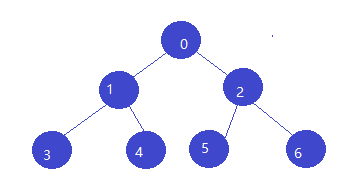
完全二叉树

1.若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。
2.如果有度为 1 的结点，那只可能有一个，且该节点只有左孩子，而无右孩子

满二叉树、完全二叉树、非完全二叉树对比

二叉排序树

形象表示

二叉排序树（Binary Sort Tree），又称二叉查找树（Binary Search Tree），亦称二叉搜索树。

定义

二叉排序树或者是一棵空树，或者是具有下列性质的二叉树：
（1）若左子树不空，则 左子树 上所有结点的值均 <= 它的 根结点 的值；
（2）若右子树不空，则 右子树 上所有结点的值均 >= 它的 根结点 的值；
（3）左、右子树也分别为二叉排序树 (递归定义)；

平衡二叉树

形象表示

定义

平衡二叉树（Self-balancing binary search tree）又被称为AVL树（有别于AVL算法），且具有以下性质：它是一棵空树或它的 左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树，同时，平衡二叉树必定是二叉搜索树，反之则不一定

二叉树性质

性质1 在二叉树的第 i 层上至多有 2^(i-1)个结点(i>=1)

用数学归纳法证明：
归纳基础：i=1时，有2^(i-1)=2^0=1。因为第1层上只有一个根结点，所以命题成立。
归纳假设：假设对所有的 j ( 1<=j < i ) 命题成立，即第j层上至多有 2^(j-1) 个结点，证明j=i时命题亦成立。
归纳步骤：根据归纳假设，第 i-1 层上至多有2^(i-2)个结点。由于二叉树的每个结点至多有两个孩子，故第 i 层上的结点数至多是第 i-1 层上的最大结点数的2倍。即 j=i 时，该层上至多有2×2^(i-2)=2^(i-1)个结点，故命题成立。

性质2 深度为k的二叉树至多有2^k-1个结点(k≥1)。

至多，即视之为满二叉树
证明：计算等比数列 2^0+2^1+…+2^(k-1)=2^k-1

性质3 在任意-棵二叉树中，若终端结点的个数为n0，度为2的结点数为n2，则no=n2+1。

回顾 m叉树的性质
1. 设m叉树中，度数为 i 的结点树为 Ni, 则总结点数为： N = N0 + N1 + … + Nm;
2. N = 分支数 + 1 , 1 为根结点
3. 于是 N = N0 + N1 + …+ Nm = 0*(N0) + 1*(N1) + … + m*(Nm) + 1
4. 对应于现在所讨论的二叉树，于是有 N = N0 + N1 + N2 = N1 + 2*(N2) + 1，于是等到结论 N0 = N2 + 1

详细证明

证明：因为二叉树中所有结点的度数均不大于2，所以结点总数(记为n)应等于0度结点数、1度结点(记为n1)和2度结点数之和：
n=no+n1+n2 (式子1)
　另一方面，1度结点有一个孩子，2度结点有两个孩子，故二叉树中孩子结点总数是：
nl+2n2
　　树中只有根结点不是任何结点的孩子，故二叉树中的结点总数又可表示为：
n=n1+2n2+1 (式子2)
　　由式子1和式子2得到：
no=n2+1

二叉树遍历

二叉树的前中后序的遍历，坐标名词针对的是根节点；无论何种遍历，左孩子永远比右孩子前

先序递归遍历 先访问根结点，再前序遍历左子树，最后前序遍历右子树。可见，这个操作的定义就是递归的

public void pre_order_traversal_recursion_way(Node root) {if (root == null) {return;}out.print(root.data + " ");pre_order_traversal_recursion_way(root.left);pre_order_traversal_recursion_way(root.right);}

中序递归遍历 先中序遍历左子树，再访问根结点，最后中序遍历右子树。由于左子树上的值都比根结点小，右子树上的值都比根结点大，所以，中序遍历一棵树所得到的结果，是从小到大有序的，可以根据这个特点，来检验你的中序遍历是否正确实现了

 void mid_order_traversal_recursion_way(Node root){if(root == null){return;}mid_order_traversal_recursion_way(root.left);out.print(root.data+" ");mid_order_traversal_recursion_way(root.right);}

后序递归遍历 先后序遍历左子树，再后序遍历右子树，最后访问根结点

void post_order_traversal_recursion_way(Node root){if(root == null){return;}post_order_traversal_recursion_way(root.left);post_order_traversal_recursion_way(root.right);out.print(root.data+" ");}

非递归先序遍历 先让根节点进栈，只要栈不为空，就可以做弹出操作；每次弹出一个结点，记得把它的左右结点都进栈。记得先右孩子，这样可以保证右子树在栈中总处于左孩子树的下面。

void pre_order_traversal_not_recursion_way(Node root) throws StackEmptyException {Stack<Node> stack = new Stack(100);Node currentNode= root;stack.push(currentNode);while (!stack.isEmpty()){currentNode = stack.pop();out.print(currentNode.data + " ");if(currentNode.right != null){stack.push(currentNode.right);}if(currentNode.left != null){stack.push(currentNode.left);}}}

非递归中序遍历

一直遍历到左子树最下边，边遍历边保存根节点到栈中
当p为空时，说明已经到达左子树最下边，这时需要出栈了
进入右子树，开始新的一轮左子树遍历(这是递归的自我实现)

private void mid_order_traversal_not_recursion_way(Node root) throws StackEmptyException {Stack<Node> stack = new Stack(100);Node currentNode = root;while (currentNode != null || !stack.isEmpty()){if(currentNode != null){stack.push(currentNode);currentNode = currentNode.left;}else{Node topNode = stack.pop();out.print(topNode.data + " ");currentNode = topNode.right;}}}

层次遍历 队列，先进先出；每出一个结点，其左右孩子进队；依此类推

 private void level_order(Node root){Queue<Node> queue = new LinkedList();Node currentNode = root;queue.add(currentNode);while (!queue.isEmpty()){currentNode = queue.poll();out.print(currentNode.data+ " ");if(currentNode.left != null){queue.add(currentNode.left);}if(currentNode.right != null){queue.add(currentNode.right);}}}