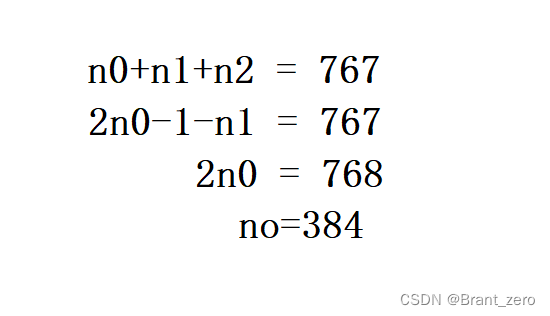在讨论一般树的存储结构及其操作之前，我们首先研究一种简单而极其重要的树结构 —— 二叉树。

二叉树的定义

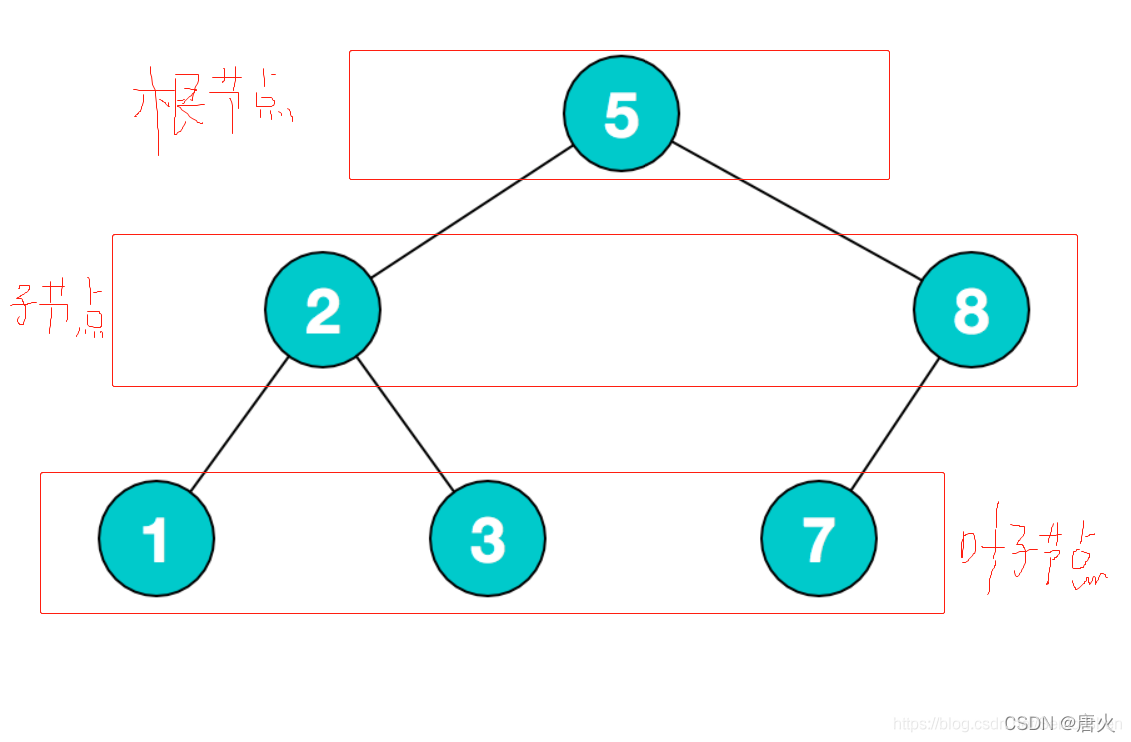
二叉树（Binary Tree） 是另外一种树型结构，它的特点是每个节点至多只有两棵子树（即二叉树中不存在度大于2的结点），并且，二叉树的子树有左右之分，其次序不能任意颠倒。

与树的递归定义类似，二叉树的递归定义如下：二叉树或者是一棵空树，或者是一棵由一个根结点和两棵互不相交的分别称为根的左子树和右子树的子树所组成的非空树。

由以上定义可以看出，二叉树中每个结点的孩子数只能是0、1或2个，并且每个孩子都有左右之分。位于左边的孩子称为左孩子，位于右边的孩子称为右孩子；以左孩子为根的子树称为左子树，以右孩子为根的子树称为右子树。

二叉树的性质

二叉树具有下列重要特性：

性质1： 在二叉树的第i层上至多有2^i-1个结点（i>=1）

利用归纳法，不难证明此性质，这里不再赘述。

性质2： 深度为k的二叉树至多有2^k-1个结点，（k>=1）.

证明：由性质1可得，深度为k的二叉树的最大结点数为：

性质3： 对任何一棵二叉树T，如果其终端结点数位n₀，度为2的结点数为n₂，则 n₀ = n₂ + 1

证明：

设n₁为二叉树T中度为1的结点数，因为二叉树中所有结点的度均小于或等于2，所以其结点总数为：

n = n₀ + n₁ + n₂

再看二叉树的分支数。除了根结点外，其余结点都有一个分支进入，设B为分支总数，则 n=B+1。由于这些分支是由度为1或2的结点射出的，所以又有 B=n₁ + 2*n₂。于是得：

n = n₁ + 2*n₂ + 1

由上述两个式子可得：

n₀ = n₂ + 1

---

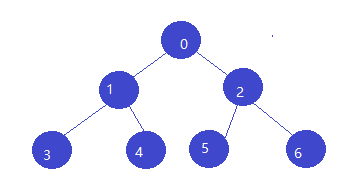
满二叉树 ：

一棵深度为k且有 2^k-1 个结点的二叉树称为满二叉树。满二叉树的特点是，每一层上的结点数都是最大结点数。

完全二叉树 ：

可以对满二叉树的结点进行连续编号，约定编号从根结点起，自上而下，自左至右。由此可以引出完全二叉树的定义。深度为k的，有n个结点的二叉树，当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应，称之为完全二叉树。

完全二叉树的特点是：（1）叶子结点只可能在层次最大的两层上出现；（2）对任一结点，若其右分支下的子孙的最大层次为l，则其左分支下的子孙的最大层次必为l或l+1。

如下图所示，（a）是一棵满二叉树，（b）是一棵完全二叉树。

---

完全二叉树将在很多场合下出现，下面介绍完全二叉树的两个重要特性.

性质4： 具有n个结点的完全二叉树的深度为 ⌊log₂n⌋+1

证明：假设深度为k，则根据性质2和完全二叉树的定义有：

2^k-1 - 1 < n <= 2^k - 1 或 2^k-1 <= n < 2^k

于是有：

k-1 <= log₂n < k，因为k是整数，所以 k = ⌊log₂n⌋+1

性质5： 如果对一棵有n个结点的完全二叉树（其深度为 ⌊log₂n⌋+1 ）的结点按层序编号（从第1层到第 ⌊log₂n⌋+1 层，每层从左到右），则对任一结点i(1<=i<=n)，有：

（1）如果i=1，则结点i是二叉树的根，无双亲；如果i>1，则其双亲PARENT(i)是结点⌊i/2⌋。

（2）如果2i>n，则结点i无左孩子（结点i为叶子结点）；否则其左孩子LCHILD(i)是结点2i。

（3）如果2i+1>n，则结点i无右孩子；否则其右孩子RCHILD(i)是结点2i+1。