【数据结构】树与二叉树的基本概念、结构特点及性质

article/2025/8/26 20:51:51

前言：本章内容主要是数据结构中树与二叉树的基本概念、结构特点及性质的引入。

文章目录

- - 树的概念
  - - 树的特点：
    - 树的常用术语：
    - 树的表示：
    - - 代码创建：
    - 树在实际中的应用：
  - 二叉树的概念
  - 特殊的二叉树
  - - 满二叉树
    - 完全二叉树
  - 二叉树的性质及其推导：
  - 练习题：
  - - - 习题1：
      - 习题2：
      - 习题3：

树的概念

数据结构中的定义的树比较有趣，它是我们所见真实树的倒置，然后再抽象的一种结构，比较有意思。同时使用树这种数据结构，可以描述现实生活中的很多事物，例如家谱、企业的组织架构等等。

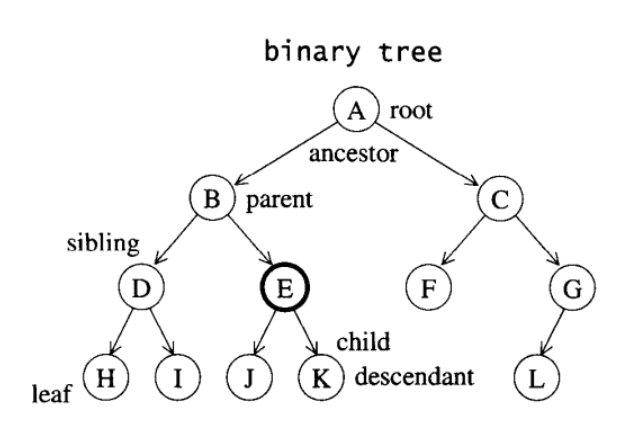
树是由n（n>=0）个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。

树的特点：

1.每个结点有零个或多个子结点；
2.没有父结点的结点为根结点；
3.每一个非根结点只有一个父结点；
4.每个结点及其后代结点整体上可以看做是一棵树，称为当前结点的父结点的一个子树；

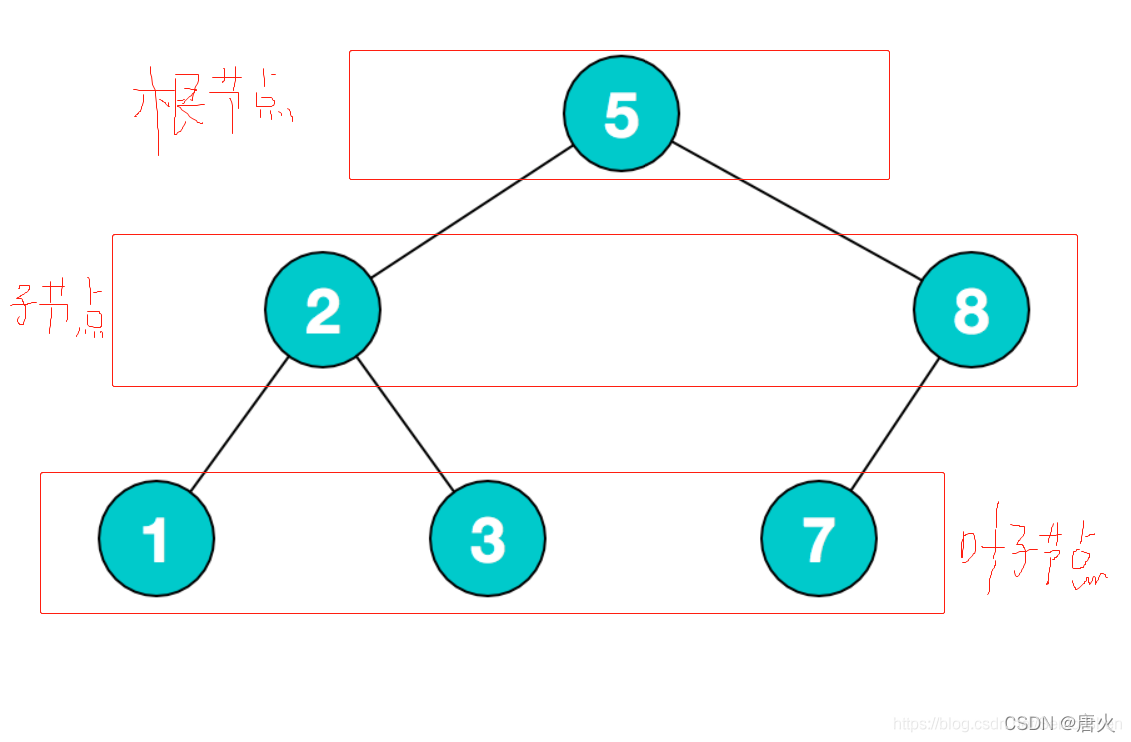
树的常用术语：

1.根结点:没有双亲节点的结点

2.孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点

3.双亲结点：若一个节点含有子节点，则这个节点称为其子节点的父节点

4.节点的度:一个节点含有的子树的个数称为该节点的度

5.叶结点：度为0的结点称为叶结点，也可以叫做终端结点

6.分支结点：度不为0的结点称为分支结点，也可以叫做非终端结点

7.结点的层次：从根结点开始，根结点的层次为1，根的直接后继层次为2，以此类推

8.结点的层序编号：将树中的结点，按照从上层到下层，同层从左到右的次序排成一个线性序列，把他们编成连续的自然数

9.树的度：树中所有结点的度的最大值

10.树的高度(深度)：树中结点的最大层次

11.森林：m（m>=0）个互不相交的树的集合，将一颗非空树的根结点删去，树就变成一个森林；给森林增加一个统一的根结点，森林就变成一棵树

12.兄弟结点：同一双亲结点的孩子结点间互称兄弟结点。

树的表示：

“左孩子右兄弟”表示法

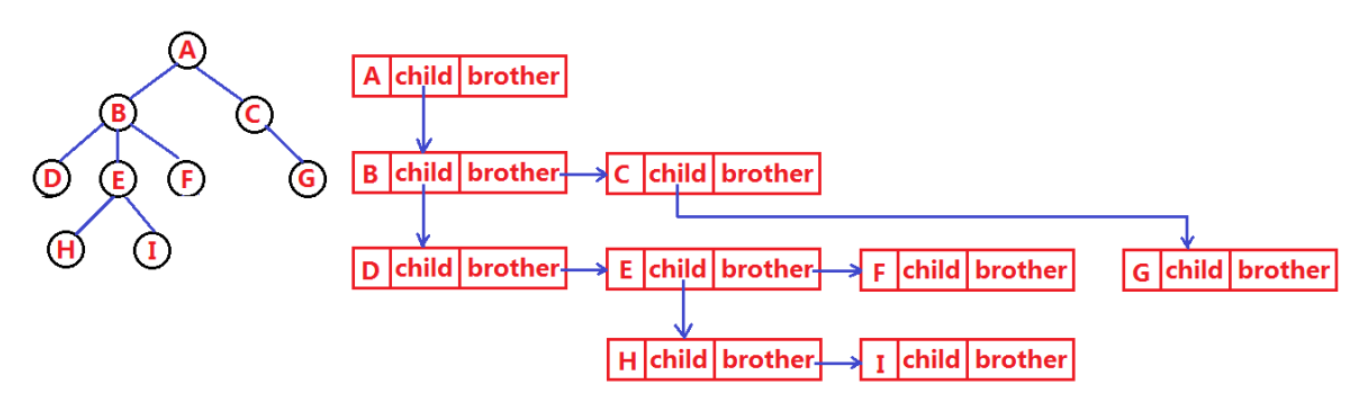
代码创建：

typedef int DataType;typedef struct node 
{struct node* child;       //指向左孩子结点struct node* brother;     //指向下一个兄弟结点DataType data;            //结构中的数据域，存储当前结点数据
}node;

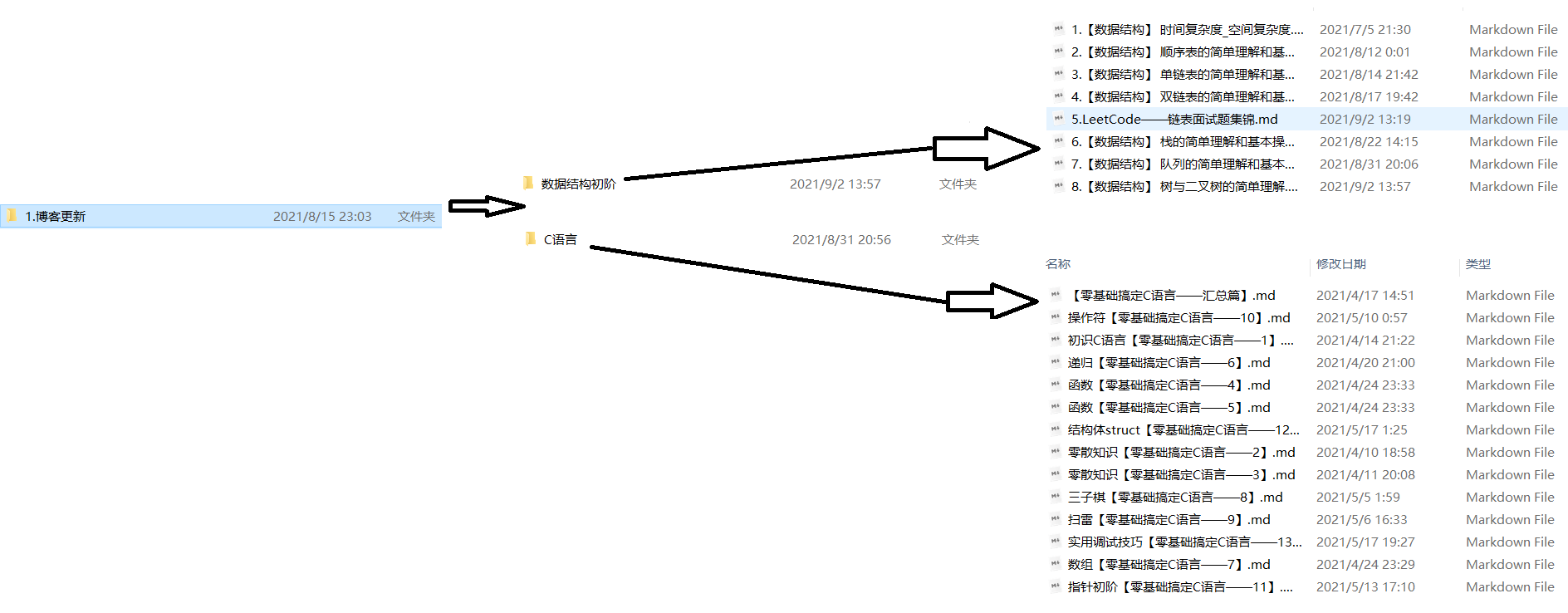
树在实际中的应用：

比如文件系统中的目录结构

二叉树的概念

一种特殊的树,见名知意，只有两个分叉的树。特点是二叉树的度最大只能为2,也就是说每个结点的子节点最多只能有两个。

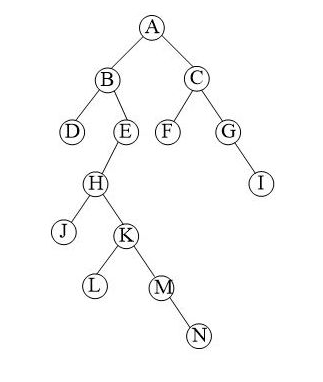
特殊的二叉树

满二叉树

核心点是 “满”

概念：每一层的结点都达到最大值**,且第n层的结点数量符合公式2^(n-1)**,层数是从1开始。

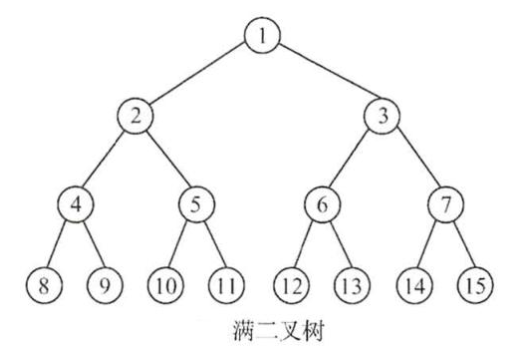
1.定义： 高度为h，并且含有(2^h)-1个结点的二叉树
2.对于编号为 i 的结点，如果有双亲，双亲为 i/2 向下取整；如果有左孩子，左孩子编号为 2i，如果有右孩子，右孩子编号为 (2i + 1)

完全二叉树

概念：对于层数(n>=2)的树,其n-1层符合满二叉树,第n层结点必须满足从左向右都连续。

比如：

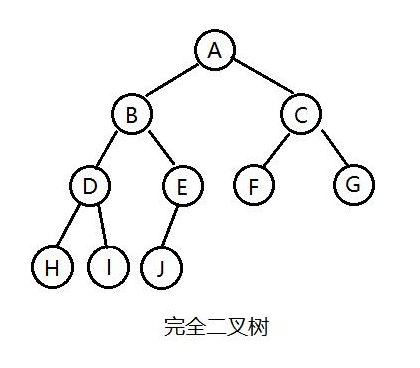
1.若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。
2.如果有度为 1 的结点，那只可能有一个，且该节点只有左孩子，而无右孩子

二叉树的性质及其推导：

性质1：二叉树第i层上的结点数目最多为 2^{i-1} (i≥1)

证明：下面用"数学归纳法"进行证明。
(01) 当i=1时，第i层的节点数目为2^{i-1}=2{0}=1。因为第1层上只有一个根结点，所以命题成立。
(02) 假设当i>1，第i层的节点数目为2^{i-1}。这个是根据(01)推断出来的！
下面根据这个假设，推断出"第(i+1)层的节点数目为2{i}“即可。
由于二叉树的每个结点至多有两个孩子，故"第(i+1)层上的结点数目” 最多是 “第i层的结点数目的2倍”。即，第(i+1)层上的结点数目最大值=2×2^{i-1}=2{i}。
故假设成立，原命题得证！

性质2：深度为k的二叉树至多有2^{k}-1个结点(k≥1)

证明：在具有相同深度的二叉树中，当每一层都含有最大结点数时，其树中结点数最多。利用"性质1"可知，深度为k的二叉树的结点数至多为：
2⁰⁺²1+…+2^k-1=2k-1
故原命题得证！

性质3：包含n个结点的二叉树的高度至少为log2 (n+1)

证明：根据"性质2"可知，高度为h的二叉树最多有2^h–1个结点。反之，对于包含n个节点的二叉树的高度至少为log2(n+1)。

性质4：在任意一棵二叉树中，若终端结点的个数为n0，度为2的结点数为n2，则n0=n2+1

证明：因为二叉树中所有结点的度数均不大于2，所以结点总数(记为n)=“0度结点数(n0)” + “1度结点数(n1)” + “2度结点数(n2)”。由此，得到等式一。
(等式一) n=n0+n1+n2
　另一方面，0度结点没有孩子，1度结点有一个孩子，2度结点有两个孩子，故二叉树中孩子结点总数是：n1+2n2。此外，只有根不是任何结点的孩子。故二叉树中的结点总数又可表示为等式二。
(等式二) n=n1+2n2+1
由(等式一)和(等式二)计算得到：n0=n2+1。原命题得证！

性质5：