NumPy下载与安装
NumPy 是 Python 的第三方扩展包,但它并没有包含在 Python 标准库中,因此您需要单独安装它。本节介绍如何在不同的操作系统上安装 NumPy。
Windows系统安装
在 Windows 系统下安装 NumPy 有两种常用方式,下面分别对其进行介绍。
使用 Python 包管理器pip来安装 NumPy,是一种最简单、最轻量级的方法。只需执行以下命令即可:
pip install numpy
在实际项目中, NumPy 通常与 SciPy 程序包一起使用,SciPy 可以看做对 NumPy 库的扩展,它在 NumPy 的基础上又增加了许多工程计算函数。因此将它们同时安装是一个不错的选择。但如果你只想针对 NumPy 进行学习,可以不用考虑这种安装方法。
注意:在 Windows 下直接使用 pip 安装 SciPy 会发生报错,需要我们解决 SciPy的依赖项问题,所以不推荐使用pip安装 SciPy 程序包。下面介绍如何使用 SciPy 栈安装。
首先我们要知道什么是 SciPy 栈?其实它是一个科学计算软件包的集成平台,这类平台囊括了常用的数值计算与机器学习库,比如 NumPy、Matplotlib、SciPy 库、IPython 等,并且它可以自动解决包之间的依赖问题。通过安装一个集成平台就可以实现上述所有软件包的安装,何乐而不为呢
下面介绍几种常用的 SciPy 栈,主要有以下几种:
Anaconda(官网下载:https://www.anaconda.com/)是一个开源的 Python 发行版,它包含了 NumPy、SciPy 等180多个科学包及其依赖项。除了支持 Windows 外,也支持 Linux 和 Mac 系统。
Anaconda 就目前应用较为广泛,因此建议安装。
Anaconda 的下载文件约 500 MB 左右,你可以选择安装 Miniconda,它是 Anaconda 的轻巧版,只需 40 余兆。
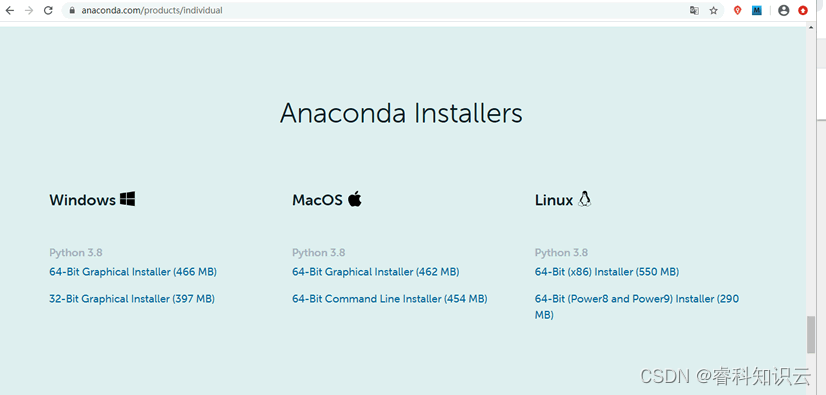
图1:Anaconda官网下载图(点击看高清图)
Python(x,y)(下载地址:https://python-xy.github.io/)是一款基于 Python、Qt (图形用户界面)和 Spyder (交互式开发环境)开发的软件,主要用于数值计算、数据分析和数据可视化等工程项目,目前只支持 Python 2 版本。
Pyzo(下载地址:https://pyzo.org/)是一个跨平台 Python IDE,基于 Python 3 编写,非常适合科学计算,它设计的宗旨就是为了简化和提供效率。
WinPython(下载地址:https://sourceforge.net/projects/winpython/files/)免费的 Python 发行版,包含了常用的科学计算包与 Spyder IDE 开发环境,但仅支持 Windows 系统。
MacOSX系统安装
Mac 系统虽然自带包管理器Homebrew,但是它不能下载 NumPy 等科学计算包,所以需要使用下列方式安装:
$ pip3 install numpy scipy matplotlib -i
https://pypi.tuna.tsinghua.edu.cn/simple
注意:-i 参数后指的是国内下载源,加快下载的速度。
Linux系统安装
在 Linux 系统中,您可以选择只单独安装 NumPy 一个软件包,也可以同时安装多个软件包。下面介绍了不同的 Linux 发行版具体的安装命令,如下所示:
1) Ubuntu/Debian
对于 Ubuntu/Debian 系统,可以在终端上执行以下命令:
$ sudo apt-get install python-numpy python-scipy python-matplotlib ipython ipython-notebook python-pandas python-sympy python-nose
2) Redhat/CentOS
在 Redhat/CentOS 系统上执行以下命令来安装 NumPy 与其它科学计算包:
$ sudo yum install numpy scipy python-matplotlib ipython python-pandas sympy python-nose
注意:不同的软件包之间必须使用“一个空格”隔开。
最后验证是否安装成功,如下所示:
打开 Python 交互解释器 ,并导入 NumPy 模块,如下图 2 所示如果未出现错误提示,则表示已安装成功。
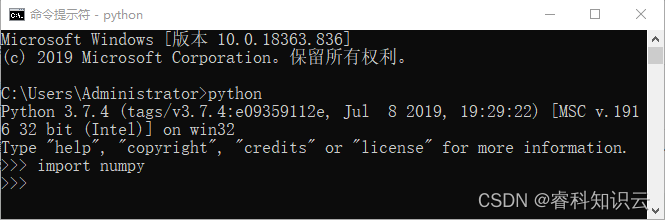
图2:Numpy安装成功
注意:这里是以 Windows 系统为例进行验证的,Linux 验证方式与其相同。