将一个给定字符串根据给定的行数，以从上往下、从左到右进行 Z 字形排列。
 比如输入字符串为 "LEETCODEISHIRING" 行数为 3 时，排列如下：
L   C   I   R
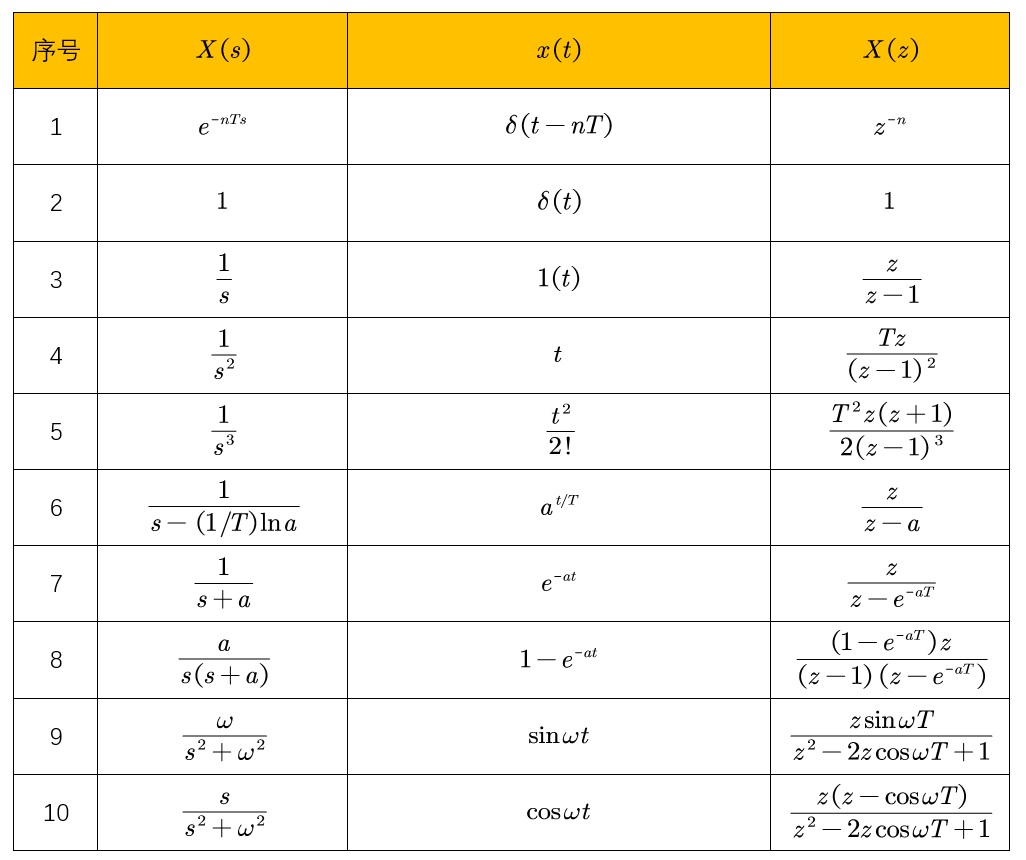
E T O E S I I G
E   D   H   N
之后，你的输出需要从左往右逐行读取，产生出一个新的字符串，比如："LCIRETOESIIGEDHN"。
请你实现这个将字符串进行指定行数变换的函数：
string convert(string s, int numRows);

示例 1:
输入: s = "LEETCODEISHIRING", numRows = 3
输出: "LCIRETOESIIGEDHN"

示例 2:
输入: s = "LEETCODEISHIRING", numRows = 4
输出: "LDREOEIIECIHNTSG"
解释:

L     D     R
E   O E   I I
E C   I H   N
T     S     G

解题思路：

如图：图中的数字是下标，i为行数，k是每一行第k个元素。

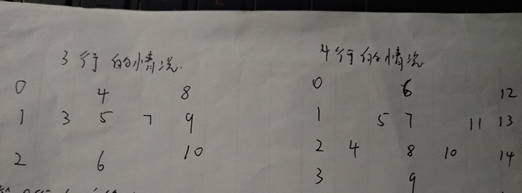
按照4行的情况来算, numRows = 4;

1.第0行的字符位于k(2*numRows-2)的位置。所对应的下标（0 ， 6， 12）

2.最后一行(numRows-1)的字符位于k(2*numRows-2)+numRows-1的位置。（3， 9，15）

3.第0行和最后一行之间第i行的字符位于k(2*numRows−2)+i 以及 (k+1)(2*numRows-2)- i处。（1， 5， 7，11， 13）

难点就是要把中间几行的规律搞清楚，就很好处理了。其实自己画一画，就能找出这些规律了。

代码实现：

class Solution {public String convert(String s,int numRows) {if( numRows == 1)return s;int temp = 2*numRows - 2;StringBuilder str = new StringBuilder();for(int i = 0; i < numRows; i++){//第0行if(i == 0){for(int k = 0; k * temp < s.length(); k++){str.append(s.charAt(k*temp));}}//第numRows-1行else if(i == numRows -1){for(int k = 0; k*temp+numRows-1 < s.length();k++){str.append(s.charAt(k*temp+numRows-1));}}//中间行else{for(int k = 0; k*temp+i < s.length(); k++){str.append(s.charAt(k*temp+i));if((k+1)*temp -i < s.length()){str.append(s.charAt((k+1)*temp - i));}}}}return str.toString();}
}

简化之后：看起来更简练。

class Solution {public String convert(String s, int numRows) {if(numRows == 1){return s;}StringBuilder ret = new StringBuilder();int n = s.length();int temp = 2 * numRows - 2;for (int i = 0; i < numRows; i++) {for (int k = 0; k + i < n; k += temp) {ret.append(s.charAt(k + i));if (i != 0 && i != numRows - 1 && k + temp - i < n)ret.append(s.charAt(k + temp - i));}}return ret.toString();}