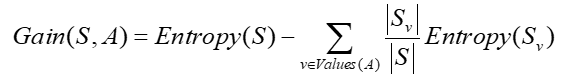最大信息系数（MIC）

article/2025/9/29 16:17:19

童鞋们觉得文章不错，就麻烦点一下下面人工智能的教程链接吧，然后随便翻阅一下

https://www.captainbed.net/qtlyx

MIC（Maximal information coefficient）一个很神奇的东西，源自于2011年发在sicence上的一个论文。

学过统计的都知道，有相关系数这么一个东西，通常叫做r。但是其实应该叫做线性相关系数，应用领域还是很窄的。而MIC这个东西呢，首先比较general，不管是什么函数关系，都可以识别，换句话说，正弦函数和双曲线函数和直线，对这个系数而言是一样的。此外还有一点，那就是，如果没有噪音的直线关系和没有噪音的正弦函数关系，他们的MIC都是1，加上相同的噪音之后，如果线性关系的MIC变成0.7了，那么正弦函数关系的MIC也变成0.7，换句话说，噪音对MIC造成的影响与变量之间的函数关系无关。当然这一论证在一篇论文中被反驳了，或者说部分反驳了。

为了说明白这个方法，首先引入一个Mutual inforamtion的东西：

是这么定义的。这里x和y是两个联系的随机变量，这个系数也可以用来衡量相关性，但是有很多缺点。比如，非均一性。不过这点在后面的论文中被推翻了，或者说，局部推翻。

p（x，y）是联合概率密度分布函数，想想就很难计算对不对，所以我们就要找一个办法来做这个事。怎么办呢？还记得蒙特卡洛么！这里有那么一点思想是这样的。

我们把两个随机变量化成散点图，然后不断的用小方格子去分割。然后计算每个方格子里面的落入概率。在某种意义上，就可以估计出联合概率密度分布了。当然，只有在数据量是无穷的情况下我们才可以认为是真的就相等了。所以，导致随后是数据量越大，MIC越好。看看第一篇nature文章的名字就知道了，Large Data Sets哦！所以如果只有几百条数据，关网页洗洗睡吧。

最后，MIC就是这么计算的。

分母下面是什么意思呢？我们之前不是对散点图残忍的分割了好多块嘛，在X方向和Y方向上就有很多段了。所以|X|就是X方向共被分成了多少段的意思。Y方向也一样。

前面还有一个限制条件，就是|X||Y|<B，也就是说，所有的方格格总数不能大于B。B又是一个什么鬼呢？很遗憾，作者说，B取数据总量的0.6或者0.55次方。

为什么?

作者表示他不想告诉你。这也没有从数学上推导出来，应该是个经验值了。

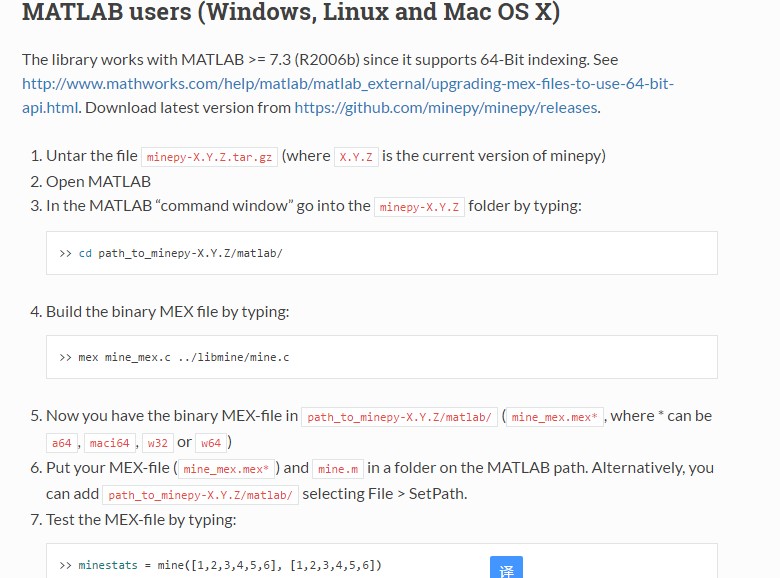
说完了，那我们来用一下吧。

装好MIC的python包，然后就可以开心的用了，不过，要注意只支持32bit的python。是不是有点蛋疼呢？所以我不能用我的Anaconda Platform了，有点小小的蛋疼呢。

好了，装python之前要好多依赖包哦，import一下，缺什么装什么吧。

import numpy as np
from minepy import MINEdef print_stats(mine):print "MIC", mine.mic()x = np.linspace(0, 1, 1000)
y = np.sin(10 * np.pi * x) + x
mine = MINE(alpha=0.6, c=15)
mine.compute_score(x, y)print "Without noise:"
print_stats(mine)
printnp.random.seed(0)
y +=np.random.uniform(-1, 1, x.shape[0]) # add some noise
mine.compute_score(x, y)print "With noise:"
print_stats(mine)

挺简单的一个例子，分别是没有噪音的正弦和有噪音的正弦。

from __future__ import division
import numpy as np
import matplotlib.pyplot as plt
from minepy import MINEdef mysubplot(x, y, numRows, numCols, plotNum,xlim=(-4, 4), ylim=(-4, 4)):r = np.around(np.corrcoef(x, y)[0, 1], 1)mine = MINE(alpha=0.6, c=15)mine.compute_score(x, y)mic = np.around(mine.mic(), 1)ax = plt.subplot(numRows, numCols, plotNum,xlim=xlim, ylim=ylim)ax.set_title('Pearson r=%.1f\nMIC=%.1f' % (r, mic),fontsize=10)ax.set_frame_on(False)ax.axes.get_xaxis().set_visible(False)ax.axes.get_yaxis().set_visible(False)ax.plot(x, y, ',')ax.set_xticks([])ax.set_yticks([])return axdef rotation(xy, t):return np.dot(xy, [[np.cos(t), -np.sin(t)],[np.sin(t), np.cos(t)]])def mvnormal(n=1000):cors = [1.0, 0.8, 0.4, 0.0, -0.4, -0.8, -1.0]for i, cor in enumerate(cors):cov = [[1, cor],[cor, 1]]xy = np.random.multivariate_normal([0, 0], cov, n)mysubplot(xy[:, 0], xy[:, 1], 3, 7, i+1)def rotnormal(n=1000):ts = [0, np.pi/12, np.pi/6, np.pi/4, np.pi/2-np.pi/6,np.pi/2-np.pi/12, np.pi/2]cov = [[1, 1],[1, 1]]xy = np.random.multivariate_normal([0, 0], cov, n)for i, t in enumerate(ts):xy_r = rotation(xy, t)mysubplot(xy_r[:, 0], xy_r[:, 1], 3, 7, i+8)def others(n=1000):x = np.random.uniform(-1, 1, n)y = 4*(x**2-0.5)**2 + np.random.uniform(-1, 1, n)/3mysubplot(x, y, 3, 7, 15, (-1, 1), (-1/3, 1+1/3))y = np.random.uniform(-1, 1, n)xy = np.concatenate((x.reshape(-1, 1), y.reshape(-1, 1)), axis=1)xy = rotation(xy, -np.pi/8)lim = np.sqrt(2+np.sqrt(2)) / np.sqrt(2)mysubplot(xy[:, 0], xy[:, 1], 3, 7, 16, (-lim, lim), (-lim, lim))xy = rotation(xy, -np.pi/8)lim = np.sqrt(2)mysubplot(xy[:, 0], xy[:, 1], 3, 7, 17, (-lim, lim), (-lim, lim))y = 2*x**2 + np.random.uniform(-1, 1, n)mysubplot(x, y, 3, 7, 18, (-1, 1), (-1, 3))y = (x**2 + np.random.uniform(0, 0.5, n)) * \np.array([-1, 1])[np.random.random_integers(0, 1, size=n)]mysubplot(x, y, 3, 7, 19, (-1.5, 1.5), (-1.5, 1.5))y = np.cos(x * np.pi) + np.random.uniform(0, 1/8, n)x = np.sin(x * np.pi) + np.random.uniform(0, 1/8, n)mysubplot(x, y, 3, 7, 20, (-1.5, 1.5), (-1.5, 1.5))xy1 = np.random.multivariate_normal([3, 3], [[1, 0], [0, 1]], int(n/4))xy2 = np.random.multivariate_normal([-3, 3], [[1, 0], [0, 1]], int(n/4))xy3 = np.random.multivariate_normal([-3, -3], [[1, 0], [0, 1]], int(n/4))xy4 = np.random.multivariate_normal([3, -3], [[1, 0], [0, 1]], int(n/4))xy = np.concatenate((xy1, xy2, xy3, xy4), axis=0)mysubplot(xy[:, 0], xy[:, 1], 3, 7, 21, (-7, 7), (-7, 7))plt.figure(facecolor='white')
mvnormal(n=800)
rotnormal(n=200)
others(n=800)
plt.tight_layout()
plt.show()

最后的效果就是这样的。很明显可以看到，左下角那个有点像三角函数的关系，Pearson系数(就是线性相关系数)为0，而MIC则有0.8。

MIC的资料：

[1]Detecting novel associationsin large data sets

[2]Equitability Analysis of theMaximal Information Coefficient, with Comparisons
[3]Equitability, mutual information, and themaximal information coefficient

童鞋们觉得文章不错，就麻烦点一下下面人工智能的教程链接吧，然后随便翻阅一下

https://www.captainbed.net/qtlyx