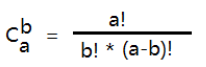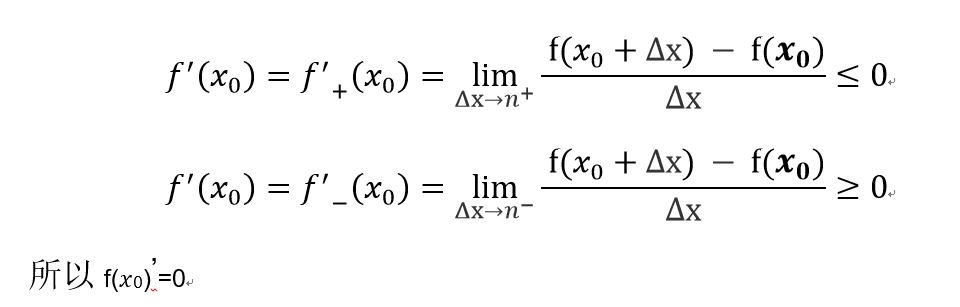前言

本文主要讨论RabbitMQ消费者的ack和nack机制，并且关注ack和nack使用上的问题记录，必要大家踩坑。

在这里插入图片描述

一、ACK机制

当生产者的发送消息到exchange，并路由到对应的队列后，MQ主动push消息到channel，由应用线程从channel中获取消息。
在这里插入图片描述

二、主动ACK

主动ACK是指在MQ主动push到channel中后，channel立马自动的给到MQ ack响应，然后MQ删除消息。
MQ使用的问题点：
1、当消费者宕机的情况下，会导致消息丢失，因为MQ已经删除了对应的消息。
2、只要队列中存在消息，MQ就会全部推送给消费者的channel。如果数据量过大，存在拖垮消费者的风险。

所以，一般使用MQ的时候选择使用手动ACK避免因消费者宕机等异常情况，导致消息丢失。

三、手动ACK

手动ACK即需要消费者主动的调用channel.ack()去通知MQ集群删除消息。
为了解决上面的第二个问题，手动ACK，一般需要搭配channel.basicQos()一起使用。Qos指的是预取量。即MQ每次发送给channel的未确认数量。
使用手动ACK也会出现如下的问题：
1、当消费逻辑发生异常后，消费者一直未主动调用channel.basicAck()，导致MQUnack数量骤升，导致MQ性能下降，甚至崩溃。
2、使用Qos，但是消费逻辑失败，未主动Ack，导致Mq unack的数量超过Qos的值。MQ将不再给消费者分配消息，阻塞整个队列，导致消息推积。

为了解决上面消费失败未主动ACK问题：
思路便是：
捕获消费处理的异常，消费成功调用channel.basicAck(). 消费失败时调用channel.basicNack()告诉MQ，消息消费失败了。

四、Nack机制

但是使用channel.basicNack又会引发另外的问题：
问题是当调用channel.basicNack后，消息会被重新存放的MQ队列的头部。下一步又消费这条会出异常的消息，又出错，塞回队列……
进入了死循环了，当然新的消息不会消费，导致堆积了。

为了解决消费失败后死循环的问题
1.创建死信队列，消费失败后通过调用channel.basicReject()进入死信队列。
2.消费失败后，存入存储中间件(Mysql , redis)等进行重试消费。

五、MQ unack的影响

接下来我们来分析下MQ中unack的数量过多的影响。
RabbitMq的设计就是允许消费者客户端很久不做ack，所以对于unack的消息，RabbitMQ并不会主动的去删除消息。并且MQ的的unack消息是存放在内存的，当队列中unack消息过多，会占用大量内存，导致MQ性能下架。除非consumer断连。这些unack的消息才会重新回到reday状态。

总结

为了解决上述使用RabbitMQ-ack的问题。
1、为了提供消息可靠性，应该使用RabbitMQ的手动Ack。
2、选择合适Qos值，一般建议100-300。太少可能存在队列推积，太多会占用MQ的内存。
3、当消费失败后，不能使用channel.basicNack() ，应该配合死信队列和存储中间件进行重试。
4、开启手动ACK后需要及时主动ack,避免因MQ unack数量骤升导致的MQ性能下降。