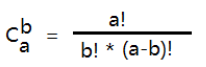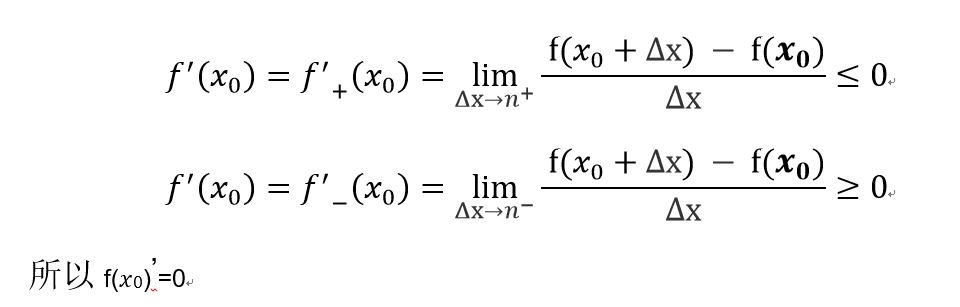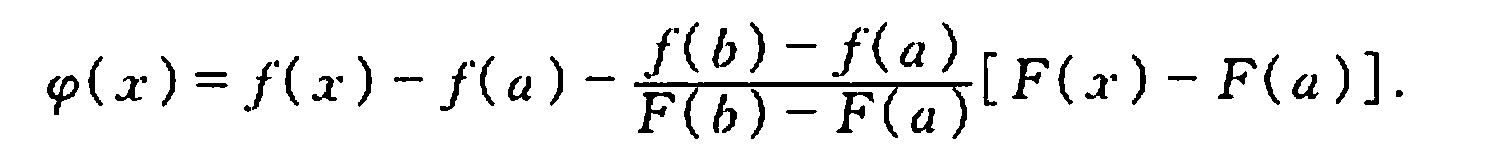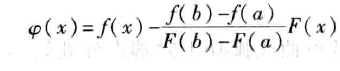本目录提供老猿Python所有相关博文的一级目录汇总,带星号的为付费专栏:
一、专栏列表
本部分为老猿所有专栏的列表,每个专栏都有该专栏置顶的博文目录:
- Python基础教程目录
- PyQt入门学习
- * 使用PyQt开发图形界面Python应用
- PyQt+moviepy音视频剪辑实战
- *moviepy音视频开发专栏
- OpenCV-Python图形图像处理
- *OpenCV-Python初学者疑难问题集
- 小白学爬虫
- *Python爬虫入门
- n行Python代码系列
- 5G基础知识学习
- 人工智能数学基础
- 零基础学区块链
二、各专栏博文目录
本部分即为上面说的各专栏文档目录列表:
- Python基础教程博文目录
- PyQt入门学习博文目录
- * 使用PyQt开发图形界面Python应用博文目录
- PyQt+moviepy音视频剪辑实战博文目录
- *moviepy音视频开发博文目录
- OpenCV-Python图形图像处理 博文目录
- *OpenCV-Python初学者疑难问题集 博文目录
- web前端开发小白学爬虫博文目录
- *Python爬虫入门专栏文章目录
- n行Python代码系列专栏文章目录
- 5G基础知识学习博文目录
- 人工智能数学基础专栏目录
- 零基础学区块链博文目录
三、汇总目录
- 老猿Python博文按标题排序汇总目录
- 老猿博客首页
声明:
- 本人还比较勤奋,因此博文有点多,但绝大多数是原创,部分文章存在灌水的情况,也是通过将长文的关键知识点单独发布出来好提高搜索率,如果要完全使用别人的博文知识,会说明转载和转载原文的地址,如果是一些网上不错文章,会在博文内标记参考博文的地址;
- 本人的博文专栏(Python、爬虫、PyQt、moviepy、5G等)都是自己零基础开始学习、研究和验证后整理而成的,从知识层面上都可以说是入门的知识,因此更适合有一定计算机基础知识的初学者学习;但这些专栏都是有自己或多或少的独特见解,是老猿进行了很多的细节研究后的知识总结,有些知识点是老猿多方查阅资料、反复测试验证甚至阅读源码(如moviepy)之后整理出来的,例如已经完结的PyQt相关专栏提供的知识点个人认为目前为止很多是网上包括Qt和PyQt介绍文章都没有的,并且还非常系统和完整,moviepy和5G也准备做成这样的;
- 本人的收费专栏文章都有对应的免费专栏,只是收费专栏的内容更深入、或案例更多,收费和免费内容范围基本一致,只是收费专栏的文章介绍更具体、内容更深入、案例更多。
对于缺乏Python基础的同仁,可以通过老猿的免费专栏《专栏:Python基础教程目录》从零开始学习Python。
如果有兴趣也愿意支持老猿的读者,欢迎购买付费专栏。
如果对文章内容存在疑问,可以在博客评论区留言,或关注:老猿Python 微信公号发消息咨询。
关于老猿的付费专栏
- 付费专栏《https://blog.csdn.net/laoyuanpython/category_9607725.html 使用PyQt开发图形界面Python应用》专门介绍基于Python的PyQt图形界面开发基础教程,对应文章目录为《 https://blog.csdn.net/LaoYuanPython/article/details/107580932 使用PyQt开发图形界面Python应用专栏目录》;
- 付费专栏《https://blog.csdn.net/laoyuanpython/category_10232926.html moviepy音视频开发专栏 )详细介绍moviepy音视频剪辑合成处理的类相关方法及使用相关方法进行相关剪辑合成场景的处理,对应文章目录为《https://blog.csdn.net/LaoYuanPython/article/details/107574583 moviepy音视频开发专栏文章目录》;
- 付费专栏《https://blog.csdn.net/laoyuanpython/category_10581071.html OpenCV-Python初学者疑难问题集》为《https://blog.csdn.net/laoyuanpython/category_9979286.html OpenCV-Python图形图像处理 》的伴生专栏,是笔者对OpenCV-Python图形图像处理学习中遇到的一些问题个人感悟的整合,相关资料基本上都是老猿反复研究的成果,有助于OpenCV-Python初学者比较深入地理解OpenCV,对应文章目录为《https://blog.csdn.net/LaoYuanPython/article/details/109713407 OpenCV-Python初学者疑难问题集专栏目录 》
- 付费专栏《https://blog.csdn.net/laoyuanpython/category_10762553.html Python爬虫入门 》站在一个互联网前端开发小白的角度介绍爬虫开发应知应会内容,包括爬虫入门的基础知识,以及爬取CSDN文章信息、博主信息、给文章点赞、评论等实战内容。
前两个专栏都适合有一定Python基础但无相关知识的小白读者学习,第三个专栏请大家结合《https://blog.csdn.net/laoyuanpython/category_9979286.html OpenCV-Python图形图像处理 》的学习使用。
对于缺乏Python基础的同仁,可以通过老猿的免费专栏《https://blog.csdn.net/laoyuanpython/category_9831699.html 专栏:Python基础教程目录)从零开始学习Python。
如果有兴趣也愿意支持老猿的读者,欢迎购买付费专栏。
如果有问题咨询,请关注老猿Python微信公众号发消息咨询: