1.nack 简介

       webrtc 中nack是最基本的QOS策略，与ack机制不同的地方是nack是接收端检测到丢包时，告知发送端具体丢包的序号，接收端收到nack后从缓存中找到对应的包并发送出去。

2. nack实现

 

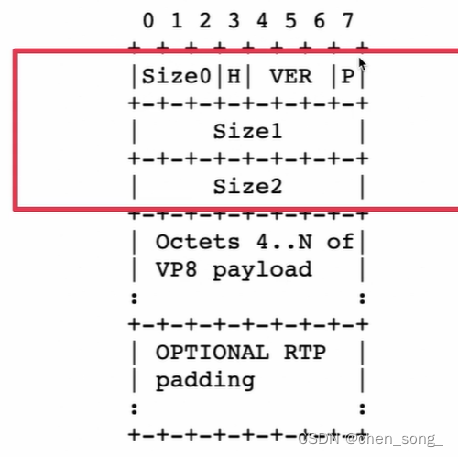
nack rtcp报文格式如上图所示，pt=205。Packet identifier(PID) 为丢包起始参考值，Bitmap of Lost Packets(BLP)为16位的bitmap，对应为1的为表示丢包数据，具体如下抓包分析：

 

Packet identifier(PID)为176。Bitmap of Lost Packets(BLP)：0x6ae1。解析的时候需要按照小模式解析，0x6ae1对应二进制：110101011100001倒过来看1000 0111 0101 0110。按照1bit是丢包，0bit是没有丢包解析，丢失报文序列号分别是：176 177 182 183 184 186 188 190 191与wireshark解析一致，当然pid和blp可以有多个。

nack实现一般会维护如下几个序列：

nacklist（missing_seq_nums）	存储丢失rtp包（比如当前序号5，下一个序号10，那么6,7,8,9都会放到nacklist中）
recoveredList	存储重传包(防止需要重传的包已经在重传包中了，重传包有可能优先过来)
keyFrameList	存储当前关键帧序号（当nacklist太超过最大长度时候，删除关键帧前面的序号，如果还不能满足需要强制I帧，保证画面不会黑屏，出现跳帧）

3.nack重要细节

1）丢包序列长度

        nacklist webrtc 中默认1000

2）每个包多久nack一次

      一个rtt时间nack一次，接收端rtt可以通过XR扩展计算获取。

3）每个包nack多少次

     默认10次

参考文献

1)https://www.jianshu.com/p/a7f6ec0c9273