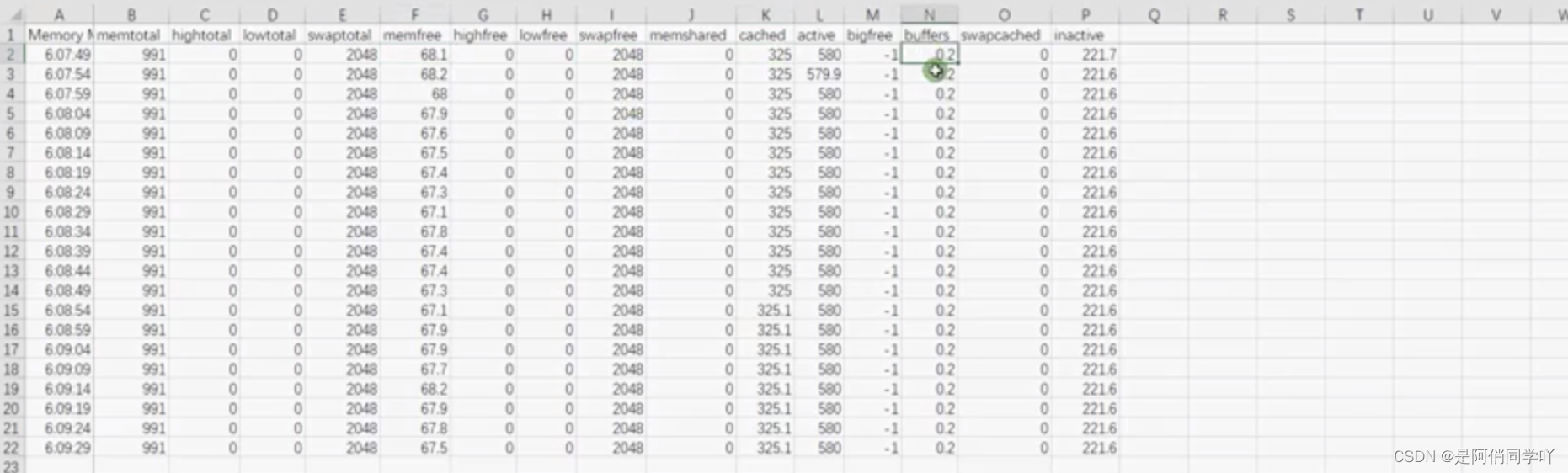
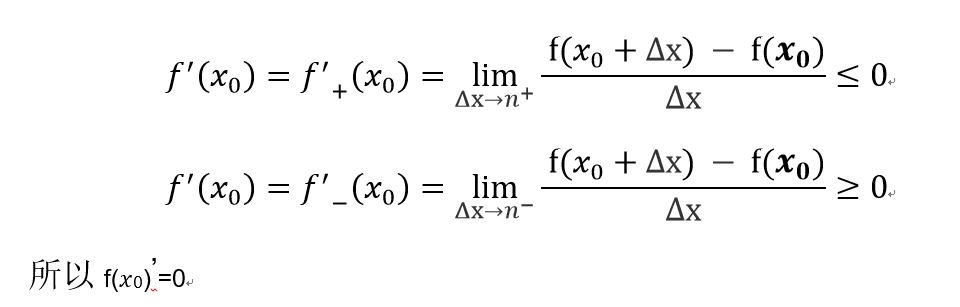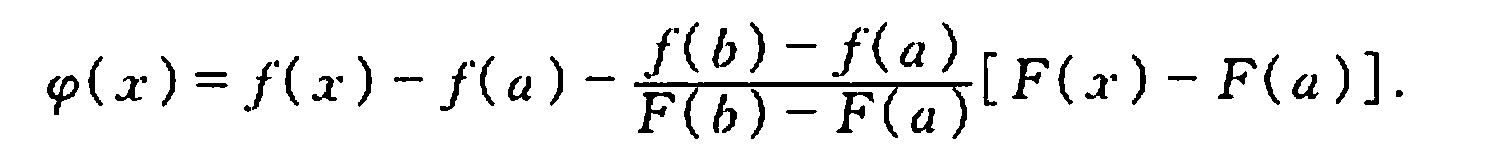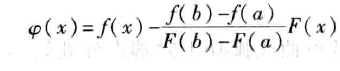流媒体弱网优化之路(NACK)——纯NACK方案的优化探索

article/2025/10/6 16:27:01

流媒体弱网优化之路(NACK)——纯NACK方案的优化探索

——
我正在的github给大家开发一个用于做实验的项目 —— github.com/qw225967/Bifrost目标：可以让大家熟悉各类Qos能力、带宽估计能力，提供每个环节关键参数调节接口并实现一个json全配置，提供全面的可视化算法观察能力。欢迎大家使用
——

文章目录

  • 流媒体弱网优化之路(NACK)——纯NACK方案的优化探索
  • 一、NACK简介
  • 二、Nack的理解
    • 2.1 一种补救策略
    • 2.2 什么时候要？
    • 2.3 要多少？
    • 2.4 怎么要？
  • 三、计算分析
    • 3.1 rtt强相关
    • 3.2 补包次数计算
    • 3.3 Nack的定时发送
    • 3.4 nack重传限制
  • 四、实验
    • 4.1 实验参数：
    • 4.2 方案一结果：
    • 4.3 方案二结果：
    • 4.4 结果分析
  • 五、总结

  近期在针对纯丢包场景做一些简单的探索实验，一个让我困扰的问题就是：不使用FEC而只是通过纯NACK进行补偿，到底能在实验环境下抵抗多少的丢包呢？每一次丢包补偿的最大时长是多久呢（一个包在发生丢包状态下补回的时长）？就此问题我展开了一系列的分析和简单的实验demo，demo放在我的github上。

一、NACK简介

  ACK是到达通知技术。以TCP为例，他可靠因为接收方在收到数据后会给发送方返回一个“已收到数据”的消息（ACK），告诉发送方“我已经收到了”，确保消息的可靠。

  NACK也是一种通知技术，只是触发通知的条件刚好的ACK相反，在未收到消息时，通知发送方“我未收到消息”，即通知未达。

二、Nack的理解

2.1 一种补救策略

  nack是常用的丢包补救策略。作为最简单、最常用的补救方式，已经被各大音视频厂商进行了大量的实验和研究。集合 zego、网易云信、百度云等厂商的实现/文章，我们将Nack策略作一些关键归纳。总结起来无非以下几点：什么时候要、要多少、怎么要？

2.2 什么时候要？

  nack作为接收方反馈的方式，要达到两个目的：
   ■ 及时找上行要丢失的数据；
   ■ 优先要最重要的数据。
  因此在设计上，我们需要：数据新旧的时序性、旧数据淘汰机制、关键数据的识别机制。在数据丢失的第一时间甚至只是乱序到达我们都开始去做重传。

2.3 要多少？

  nack是rtcp数据，属于控制信息。信令在整个传输中流量的占比应该严格控制，目前网络的做法，rtcp信令可能只占到整体流量的5%左右，xx公司则是会达到近10%的占比（包含了各类带宽估计的feedback），而某著名媒体服务商也达到了12%。每个nack数据包最大也只为网络传输的MTU大小（1500字节），如果按20ms的定时要nack，传输数据量每秒50个包，每个包可以携带约300 ~ 400个seq（xx公司是347个）。因此计算得到一秒最大可以要将近15000 ~ 20000个数据包。往往我们1.2m的码率每秒也只有500 - 600个包，因此我们在整个传输中间我们向上行索要seq号有部分是重复的。
  经验归纳出来：
  ■ 在带宽允许的情况下，要保证能补就补，尽量延迟超时机制；
  ■ 在索要seq的数量上做一个最大的控制量，某著名媒体服务商在70%丢包的环境下会索要最高达27次。

2.4 怎么要？

  nack请求哪些seq也是非常重要的。我们常用的会分为两类：
   ■ 视频数据：关键帧、非关键帧
   ■ 音频数据。关键帧数据肯定是需要更多优先级倾斜的，相比于普通数据，他要的次数更多，大约多40%。而音频数据较小，在整体传输中流畅率是比较好保证的，因此即使维持在普通传输的重传频率上依然能保证较好的流畅性。
同时，请求的时机也很关键，实验证明，前松后紧的策略可以有效提高抗丢包性能（前面要的频率低，如果还没补上则越要越快）

三、计算分析

3.1 rtt强相关

在这里插入图片描述
  上图的过程是一个假设在30%数据丢包率，40ms定时nack的状态下请求包的过程。
   ■ 时间为0ms的时候：sdk1发送20个数据包，sdk2因为丢包30%接到了14个；
   ■ 等待40ms定时器触发时：nack里的seq有6个；
   ■ 到60ms时：sdk1接到了sdk2的nack信令，立刻传出6个数据包；
   ■ 80ms时：sdk1再次发出16个数据包（10个正常数据+6个丢包数据），但实际到达sdk2的又少了5个——11个。通过计算可知，其中nack索要的包再次丢失的概率为11%。（向上取整的方式）

3.2 补包次数计算

  (不做重传限制)计算：16 x 30% x 6/16 ≈ 2个。这2个包可能再次丢失，加入到下次的重传过程中。也就是下次重传会有6个本次丢失的流数据包和2个前一次丢失的数据包，也就是8个。按这个累计计算，下次再丢失第一个的概率是：18 x 30% x 2/18 ≈ 1个。最后会再重传一次，也就是时间戳0ms的数据可能经过3次重传才能理论上完全补上，因此是：160ms时长，最少三次重传，才能保证在30%丢包的网络中实现补包。
  （有一个rtt的重传限制的话），那么很有可能二次丢失的包会再次时延一个rtt之后再重传，可能会导致时延增大。
虽然理论上最少使用3次重传就可以抵抗30%丢包，但实际测试中，往往有部分数据会消耗更多的重传次数，而大部分数据可以在2次重传就补回。

3.3 Nack的定时发送

提示：此处讨论的是定时做nack重传的方式，而非丢失立即重传的方式。（该方式在webrtc中使用）

  我们可知，nack定时器的时间40ms和RTT时间是一致的时候我们可以保证在3次重传下抵抗30%的丢包。线上一般rtt可能小于40ms，如果定时器继续维持40ms则有可能导致不能及时重传数据。因此在nack定时器的粒度上我们应该尽量维持较细的粒度，然后通过重传时间计算该次是否需要重传对应的seq数据。

3.4 nack重传限制

  数据是连续性到达，我们对哪些数据该发应该做接收时间记录。比如刚加入丢失队列的数据，理应等待一段时间再重传，这样就可能卡在我们定时器的最后时刻导致该包多等待一个周期。（以上图为例，这段可以这么理解：发包间隔是2ms，那么理论上下一个包到达的速度应该是2ms，当他能连续在RTT/10(2ms) ~ RTT/2(20ms)的时间内到达是正常的，当大于 RTT/2可能已经丢失，如果等到一个RTT的时间则太长了，此时实时性就会变差）。
同时，重传应该分为两种情况讨论：
   ■ 第一次丢失：我应该给予网络更多的宽容度，因为乱序到达的情况也不少，因此一般第一次丢失的情况会给RTT/2 ~ RTT的限制时间
   ■ 重复丢失：当重复丢失时我们应该意识到，重传的包在来的路上再次丢失或者我们回复的nack丢失了，无论如何我们都要尽快地去补回包，因此逐渐加快我们的频率，至少是于RTT/2或者是小于RTT/2的频率。这样虽然我们可能多发了一次nack，但是会抵抗二次丢包造成的可能，也就是把第三次丢包的发生概率降低。

四、实验

  我们实现一个发送端和接收端。发送端的功能是：不断发送序号为1-65535，大小1400的假数据包。接收端实现nack的逻辑，大致的逻辑是和mediasoup中的nack类似。具体的代码可以查看我的github：https://github.com/qw225967/transport-demo。
  这里列一下大致的nack代码，同时列出关键的影响因素：
   ■ nack定时器——单位ms；
   ■ nack限制间隔——单位ms（一般是rtt）；

/******************************************************** @author      : dog head* @date        : Created in 2022/3/2 1:52 下午* @mail        : qw225967@github.com* @project     : receiver* @file        : nack_gen.cpp* @description : TODO*******************************************************/#include "nack_gen.h"
#include "pack.h"
#include "test_tp.h"namespace transportdemo {/* Static. */constexpr size_t MaxPacketAge{ 10000u };constexpr size_t MaxNackPackets{ 1000u };constexpr uint32_t DefaultRtt{ 100u };//	constexpr uint8_t MaxNackRetries{ 10u };//	constexpr uint64_t TimerInterval{ 40u };// =================== nack test ===================constexpr uint8_t MaxNackRetries{ 20u };constexpr uint64_t TimerInterval{ 20u };// =================== nack test ===================/* Instance methods. */NackGenerator::NackGenerator() : rtt(DefaultRtt) {}NackGenerator::~NackGenerator() {}// Returns true if this is a found nacked packet. False otherwise.bool NackGenerator::ReceivePacket(TESTTPPacketPtr packet) {TESTTPHeader* header = reinterpret_cast<TESTTPHeader *>(packet->mutable_buffer());uint16_t seq    = header->get_sequence();if (!this->started) {this->started = true;this->lastSeq = seq;return false;}// Obviously never nacked, so ignore.if (seq == this->lastSeq)return false;// May be an out of order packet, or already handled retransmitted packet,// or a retransmitted packet.if (SeqLowerThan(seq, this->lastSeq)) {auto it = this->nackList.find(seq);// It was a nacked packet.if (it != this->nackList.end()) {this->nackList.erase(it);return true;}return false;}AddPacketsToNackList(this->lastSeq + 1, seq);this->lastSeq = seq;return false;}void NackGenerator::AddPacketsToNackList(uint16_t seqStart, uint16_t seqEnd) {// Remove old packets.auto it = this->nackList.lower_bound(seqEnd - MaxPacketAge);this->nackList.erase(this->nackList.begin(), it);// If the nack list is too large, remove packets from the nack list until// the latest first packet of a keyframe. If the list is still too large,// clear it and request a keyframe.uint16_t numNewNacks = seqEnd - seqStart;if (this->nackList.size() + numNewNacks > MaxNackPackets){if (this->nackList.size() + numNewNacks > MaxNackPackets){this->nackList.clear();return;}}for (uint16_t seq = seqStart; seq != seqEnd; ++seq){if (this->nackList.find(seq) == this->nackList.end())this->nackList.emplace(std::make_pair(seq, NackInfo{ seq, seq, 0, 0 }));}}double CalculateRttLimit2SendNack(int tryTimes) {return tryTimes < 3 ?  (double)(tryTimes*0.4) + 1 : 2;}std::vector<uint16_t> NackGenerator::GetNackBatch() {uint64_t nowMs = GetCurrentStamp64();NackFilter filter = NackFilter::TIME;std::vector<uint16_t> nackBatch;auto it = this->nackList.begin();while (it != this->nackList.end()) {NackInfo& nackInfo = it->second;uint16_t seq       = nackInfo.seq;auto limit_var = uint64_t( this->rtt / CalculateRttLimit2SendNack(nackInfo.retries) );if (filter == NackFilter::TIME && nowMs - nackInfo.sentAtMs >= limit_var) {//      if (filter == NackFilter::TIME && nowMs - nackInfo.sentAtMs >= this->rtt) {nackBatch.emplace_back(seq);nackInfo.retries++;auto oldMs = nackInfo.sentAtMs;if (oldMs == 0){oldMs = nowMs;}nackInfo.sentAtMs = nowMs;std::cout << "retry seq:" << seq << ", times:" << unsigned(nackInfo.retries) << ", interval:" << nowMs-oldMs << std::endl;if (nackInfo.retries >= MaxNackRetries) {it = this->nackList.erase(it);} else {++it;}continue;}++it;}return nackBatch;}void NackGenerator::Reset() {this->nackList.clear();this->started = false;this->lastSeq = 0u;}
} // namespace transport-demo

4.1 实验参数：

   弱网参数：20%随机丢包率+70ms（rtt）。
   ■ 方案一：定时40ms触发一次nack信令发送定时器，再次发送限制为：一个rtt时长。
   ■ 方案二：定时20ms触发一次nack信令发送定时器，再次发送限制为：动态变化，随着重传次数增加而增加：0.7rtt——>0.6rtt——>0.5*rtt 随后稳定。

  这样设计的目的是为了缩短包补偿的间隔，降低卡顿率。

4.2 方案一结果：

在这里插入图片描述
  如图中， 序号为：11741 —— 11496 中：约245个包。

  发生丢包的记录为：63 条。
    一次重传：46条，占比18.77%；
    二次重传：15条，占比6.12%，卡顿时长：80+35(rtt/2) = 115ms ；
    三次重传：2条，占比0.81%，卡顿时长：120+80+35(rtt/2) = 235ms；

4.3 方案二结果：

在这里插入图片描述
  如图中， 序号为：1433 —— 1720 中：约287个包。

  发生丢包的记录为：63 条。
    一次重传：58条，占比20.2%；
    二次重传：3条，占比1.04%，卡顿时长：60+35(rtt/2) = 95ms；
    三次重传：1条，占比0.35%，卡顿时长：60+60+35(rtt/2) = 155ms；
    四次重传：1条，占比0.35%，卡顿时长：60+60+60+35(rtt/2) = 215ms；

4.4 结果分析

  1.我们通过加快发送nack的频率，缩短了补包时间。在同样重传3次的情况下，我们可以缩短将近80ms的延迟；
  2.第二方案的实现中我们可以看到，即使发生了4次重传，也比之前235ms的耗时更小，而且这种表现在高延迟环境下会体现更明显。

五、总结

  在音视频传输中，使用纯nack方案来做丢包补偿是不能满足所有需求的。上述20%丢包环境下，发生3次重复性丢包的概率已经不低，假设我们不惜代价（牺牲带宽）地增大nack量。收获的效果其实并不会很好，因为不断发生的重复丢包会导致我们补包的稳定性不高。时长时短的到达包就会造成我们画面类似于ppt般的卡顿。
  因此对于纯nack方案的最佳性能，实际应用中并不理想。那么现阶段非常流行的fec+nack是如何将我们的网络质量提高到抗70%丢包并无感知的？实际就是通过不断平和fec（前向纠错）与nack的配比来实现的（即使如此，使用fec+nack也会消耗带宽为原流2倍以上的带宽才实现的）。后续我将会结合fec和nack来做一些实验FEC的实践奥秘，看看fec是如何有效的实现弱网抵抗的。那么这篇文章就到这里结束，感兴趣的同学也可以下载我nack 的demo测试一下，也许会发现更有意思的东西。


http://chatgpt.dhexx.cn/article/MYhCaqjX.shtml

相关文章

WebRTC源码分析 nack详解

WebRTC源码分析 nack详解

1、Nack过程 1.1 nack是什么 丢包重传(NACK)是抵抗网络错误的重要手段。NACK在接收端检测到数据丢包后&#xff0c;发送NACK报文到发送端&#xff1b;发送端根据NACK报文中的序列号&#xff0c;在发送缓冲区找到对应的数据包&#xff0c;重新发送到接收端。NACK需要发送端&am…
阅读更多...
谈谈网络通信中的 ACK、NACK 和 REX

谈谈网络通信中的 ACK、NACK 和 REX

目录 名词解释 问题 1&#xff1a; 接收方如何判断数据包是否丢失&#xff1f; 问题 2&#xff1a;发送方如何确认数据包已经丢失&#xff1f; 问题 3&#xff1a;重传超时的计算规则&#xff1f; 问题 4&#xff1a;发送方的数据包要缓存多久&#xff1f; 问题 5&#x…
阅读更多...
费马定理_高数_1元微积分

费马定理_高数_1元微积分

定理 设 f(x) 在 x0 点处满足&#xff1a;1、可导 2、取得极值&#xff0c;则有 f ’ (x0)0 证明 不妨假设 f(x) 在点 x0 处取得极大值&#xff0c;则存在 x0 的邻域 U( x0 )&#xff0c;对任意的 x属于U( x0 )&#xff0c;都有 根据导数定义与极限的保号性有 又 f(x) 在点…
阅读更多...
高等数学费马定理的证明

高等数学费马定理的证明

阅读更多...
老猿Python博客文章目录索引

老猿Python博客文章目录索引

本目录提供老猿Python所有相关博文的一级目录汇总&#xff0c;带星号的为付费专栏&#xff1a; 一、专栏列表 本部分为老猿所有专栏的列表&#xff0c;每个专栏都有该专栏置顶的博文目录&#xff1a; Python基础教程目录PyQt入门学习* 使用PyQt开发图形界面Python应用PyQtmo…
阅读更多...
(组合数+快速幂+lucas+费马小引理)acwing 887. 求组合数 III

(组合数+快速幂+lucas+费马小引理)acwing 887. 求组合数 III

887. 求组合数 III 题目链接https://www.acwing.com/problem/content/889/ 题目&#xff1a; 思路&#xff1a; #include<iostream> #include<cstdio> using namespace std; typedef long long LL; int n; int qmi(LL a,int k,int p){int res1;while(k){if(k&…
阅读更多...
（组合数 +快速幂+逆元+费马小引理）acwing 886. 求组合数 II

（组合数 +快速幂+逆元+费马小引理）acwing 886. 求组合数 II

886. 求组合数 II 题目链接https://www.acwing.com/problem/content/888/ 题目&#xff1a; 思路&#xff1a; #include<iostream> #include<cstdio> using namespace std; typedef long long LL; const int mod1e97;//mod为质数 int a,b,n; int fact[100010],…
阅读更多...
Leetcode-数学费马平方和定理-633. 平方数之和

Leetcode-数学费马平方和定理-633. 平方数之和

题目633. 平方数之和&#xff1a; 题解&#xff1a; 1&#xff0c;暴力枚举sqrt class Solution { public:bool judgeSquareSum(int c) {if(c < 2 ){return true;}for(long a 0; a*a < c; a){double b sqrt(c - a * a);if((int)b b){return true;}}return false;} …
阅读更多...
费马定理、罗尔中值定理、零点存在定理、拉格朗日中值定理、

费马定理、罗尔中值定理、零点存在定理、拉格朗日中值定理、

介值定理 介值定理如果AB,则开区间&#xff08;a,b&#xff09;内可能取不到端点值A,B 即介值定理如果C不等于端点值&#xff0c;那么 ξ ξ ξ可以是属于开区间&#xff0c;如果C等于端点值&#xff0c;那么 ξ ξ ξ必须属于闭区间。 零点存在定理 假设函数f(x)在闭区间[a,…
阅读更多...
费马引理的证明

费马引理的证明

设 f(x)在 ξ处最大&#xff0c;故不论Δx是正或负&#xff0c;总有 设 &#xff0c; 则 。 故由极限的保号性有 &#xff08;1&#xff09; 而当 时&#xff0c; &#xff0c; 故 &#xff08;2&#xff09; 由(1)&#xff0c;(2)两式及 存在知&#xff0c;必有 设 f(x)在 ξ处…
阅读更多...
费马引理、罗尔定理、拉格朗日中值定理

费马引理、罗尔定理、拉格朗日中值定理

算法交流群纯数学:232875138
阅读更多...
费马引理

费马引理

转载于:https://www.cnblogs.com/fuhang/p/7976329.html
阅读更多...
高等数学——微分中值定理

高等数学——微分中值定理

本文始发于个人公众号&#xff1a;TechFlow&#xff0c;原创不易&#xff0c;求个关注 今天和大家回顾一下高数当中的微分中值定理&#xff0c;据说是很多高数公式的基础。由于本人才疏学浅&#xff0c;所以对于这点没有太深的认识。但是提出中值定理的几个数学家倒是如雷贯耳&…
阅读更多...
（机器学习、人工智能数学基础：高等数学篇）第三章：微分中值定理：第一节：微分中值定理

（机器学习、人工智能数学基础：高等数学篇）第三章：微分中值定理：第一节：微分中值定理

文章目录 一&#xff1a;费马引理二&#xff1a;罗尔定理三&#xff1a;拉格朗日中值定理四&#xff1a;柯西中值定理五&#xff1a;泰勒公式&#xff08;1&#xff09;泰勒公式&#xff08;2&#xff09;常见泰勒展开式 一&#xff1a;费马引理 费马引理&#xff1a;如果函数…
阅读更多...
高等数学（总结1-导数的几个定理）

高等数学（总结1-导数的几个定理）

1&#xff09;费马引理&#xff1a; 证明的关键&#xff1a;如果在x0处可导&#xff0c;则在x0处的左导数等于右导数等于导数。 意义&#xff1a;显然(x0&#xff0c;f(x0))是f(x)在x0邻域内的一个极值点&#xff0c;推广&#xff1a;f(x)的极值点&#xff08;驻点&#x…
阅读更多...
人工智能数学基础：费马引理、罗尔定理、拉格朗日微分中值定理、柯西中值定理

人工智能数学基础：费马引理、罗尔定理、拉格朗日微分中值定理、柯西中值定理

一、费马&#xff08;Fermat&#xff09;引理 费马&#xff08;Fermat&#xff09;引理&#xff1a;设函数f(x)在点x0的某邻域U(x0)内有定义&#xff0c;并且在x0处可导&#xff0c;如果对任意的x∈U(x0)&#xff0c;有f(x)≤f(x0)(或f(x)≥f(xo))&#xff0c;那么f’(x0)0。 …
阅读更多...
nmon结果分析工具_使用nmon analyzer 分析指标

nmon结果分析工具_使用nmon analyzer 分析指标

监控结果分析 使用nmon analyser对nmon文件进行解析&#xff0c;生成带图表信息的xlsx格式文件。 下载地址&#xff1a;http://nmon.sourceforge.net/pmwiki.php?nSite.Nmon-Analyser nmon analyser转换数据 进入工具目录&#xff0c;双击nmon analyser vxx_x.xlsm格式文件&…
阅读更多...
Linux数据存储监控工具 - nmon

Linux数据存储监控工具 - nmon

nmon介绍 nmon 是 IBM 公司开发的 Linux 性能监控工具&#xff0c;可以实时展示系统性能情况&#xff0c;也可以将监控数据写入文件中&#xff0c;并使用 nmon 分析器做数据展示。 nmon 可监控的数据类型 CPU使用率内存使用情况磁盘适配器文件系统中的可用空间页面空间和页面速…
阅读更多...
nmon下载及使用方法

nmon下载及使用方法

nomn官方文档&#xff1a;http://www.ibm.com/developerworks/cn/aix/library/analyze_aix/ nomn下载页面&#xff1a; AIX:https://www.ibm.com/developerworks/community/wikis/home?langen#!/wiki/Power%20Systems/page/nmon Linux: nmonanalyser 下载页面&#xff1a;http…
阅读更多...
nmon使用及监控数据分析

nmon使用及监控数据分析

【使用】 【监控数据分析】 参考链接&#xff1a;nmon监控数据分析 性能测试中,各个服务器资源占用统计分析是一个很重要的组成部分,通常我们使用nmon这个工具来进行监控以及监控结果输出。 一、在监控阶段使用类似下面的命令 ./nmon -f write_3s_20vu.nmon -t -s 30 -c 100 进…
阅读更多...
推荐文章

Copyright @ 2022~2023