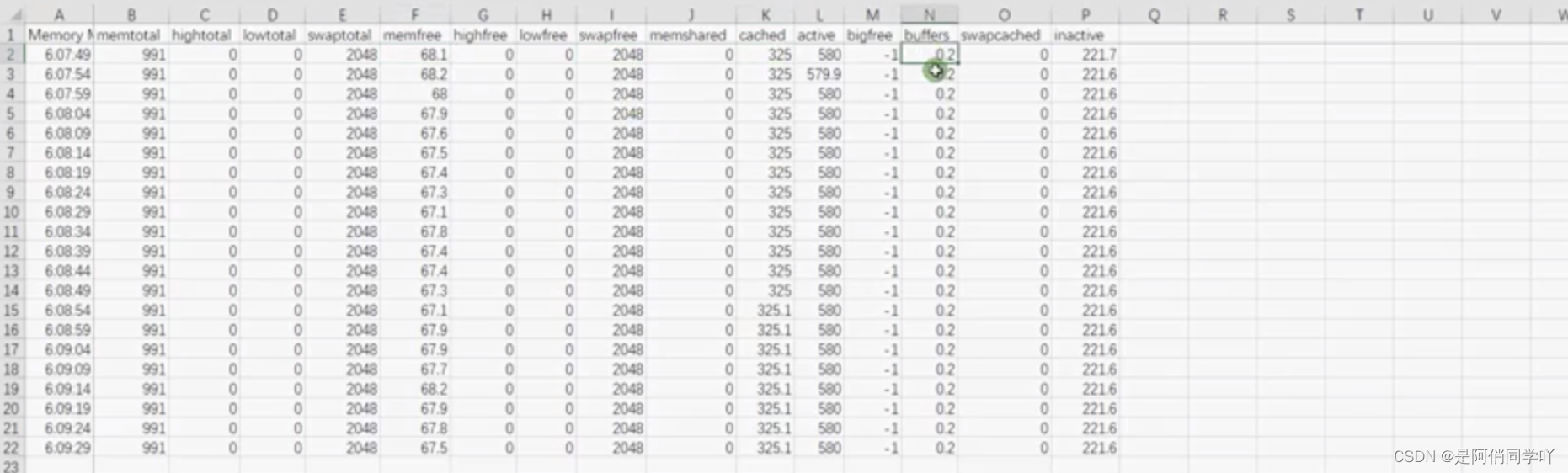
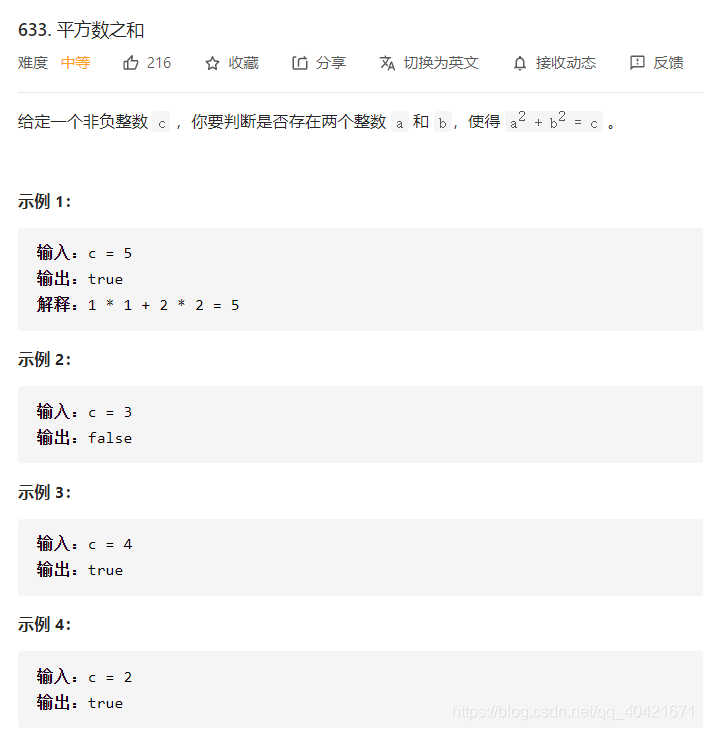
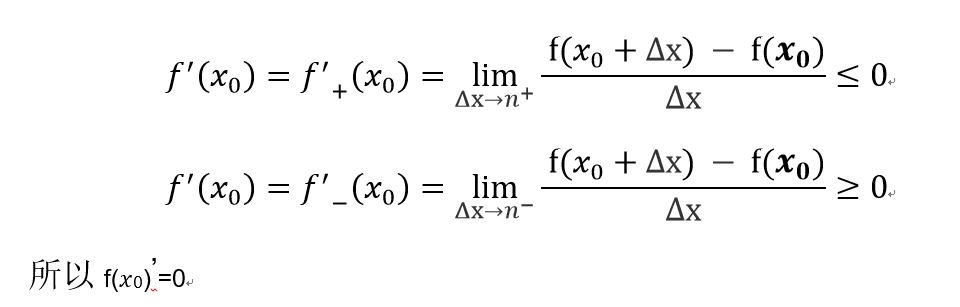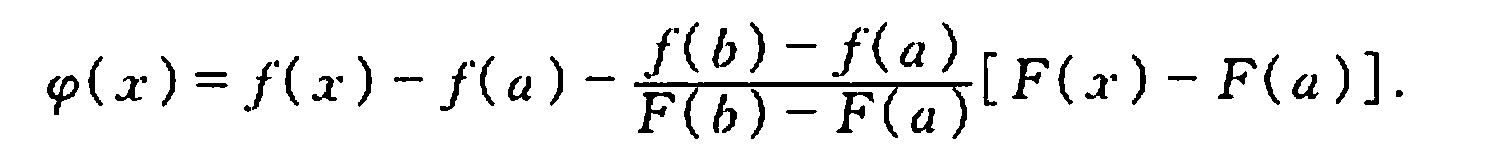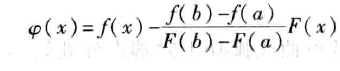题目633. 平方数之和：

题解：

1，暴力枚举+sqrt

class Solution {
public:bool judgeSquareSum(int c) {if(c <= 2 ){return true;}for(long  a = 0; a*a <= c; a++){double b = sqrt(c - a * a);if((int)b == b){return true;}}return false;}
};

2，双指针

为什么双指针不会错过正确答案？本质是二维矩阵搜索

class Solution {
public:bool judgeSquareSum(int c) {if(c <= 2 ){return true;}int l = 0, r = sqrt(c)+1;while(l < r){int mid = (l+r)/2;if( (float)sqrt(c-mid*mid) == (int) sqrt(c-mid*mid)) {return true;}else{r = mid-1;}}return false;}
};

3，费马平方和定理

class Solution {
public:bool judgeSquareSum(int c) {for (int base = 2; base * base <= c; base++) {// 如果不是因子，枚举下一个if (c % base != 0) {continue;}// 计算 base 的幂int exp = 0;while (c % base == 0) {c /= base;exp++;}// 根据 Sum of two squares theorem 验证if (base % 4 == 3 && exp % 2 != 0) {return false;}}// 例如 11 这样的用例，由于上面的 for 循环里 base * base <= c ，base == 11 的时候不会进入循环体// 因此在退出循环以后需要再做一次判断return c % 4 != 3;}
};