python解常微分方程
python解常微分方程的步骤如下:
- 将计算区间分为n个小段,在每一小段上将求解的曲线作为直线处理;
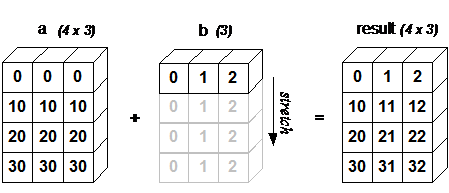
- 将一个n阶常微分方程转换成[y_n,y_n-1,…,y_i,…,y_0]向量的线性方程组,其中y_i表示y的i阶导数;
- 确定初始状态
- 迭代求解每一个点的y值(欧拉法),最后通过matplotlib做出曲线图。
以下面的三阶常系数微分方程为例:
1. 假设求解区间为0~4,划分为400个小区间
2. 转换成对应的线性方程组,如下图
3. 初始状态设为y2_0 = 2, y1_0 = 1, y0_0 = 0
4. 求解及出图,见代码
from scipy.integrate import odeint
import numpy as np
import matplotlib.pyplot as plty2_0 = 2
y1_0 = 1
y0_0 = 0
y0 = [y0_0, y1_0,y2_0]# 函数func,y是指上面提到的有y的各阶导数组成的向量,t是指自变量
def func(y, t):T=[[1,1,1], [1,0,0],[0,1,0]]return T@yx = np.arange(0, 4.0, 0.1)
t=x
y = odeint(func, y0, t)print(x)
print(y)plt.plot(x,y[:,0])
plt.show()
结果如下:
python求解点绕定轴转动后的坐标
用python计算定点绕定轴转动一定角度的坐标,输出结果如下:
import numpy as npdef main():x = np.array([1,0,0])y = np.array([0,1,0])z = np.array([0,0,1])axis_in = input('Enter the coordinates of rotation axis:\n')axis = np.array([np.float(n) for n in axis_in.split()])#print (axis)angle_in = input('Enter the rotation angle:\n')angle = np.float(angle_in)*np.pi/180#print (np.degrees(angle)) point_in = input('Enter the coordinates to be rotated:\n')point = np.array([np.float(n) for n in point_in.split()])#print (point)axis1 = np.array([axis[0],axis[1],0])theta = np.arccos((axis1@x)/np.linalg.norm(axis1))print ('theta: ', np.degrees(theta))t1 = np.array([[np.cos(-theta), -np.sin(-theta),0], [np.sin(-theta), np.cos(-theta),0], [0, 0, 1]])#zprint ('coordinates transform matrix:\n', t1)point1 = t1@pointprint ('transformed coordinates I:\n', point1)phi = np.arccos((axis@z)/np.linalg.norm(axis))print ('phi: ', np.degrees(phi))t2 = np.array([[np.cos(-phi), 0, np.sin(-phi)], [0, 1, 0], [-np.sin(-phi), 0, np.cos(-phi)]])#yprint ('coordinates transform matrix:\n', t2)point2 = t2@point1print ('transformed coordinates II:\n', point2)t3 = np.array([[np.cos(angle), -np.sin(angle),0], [np.sin(angle), np.cos(angle),0], [0, 0, 1]])#zprint ('rotation matrix under new coordinates:\n', t3)rotation = np.transpose(t1) @ np.transpose(t2) @ t3 @ t2 @ t1print ('rotation matrix under original coordinates:\n', rotation)point_rotated = rotation @ np.transpose(point)print ('the coordinates of rotated point is: \n', point_rotated)if __name__ == "__main__":main()
python绘制球面渐开线
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3Dr_theta=np.radians(45)
l=1000cr,ctheta=np.mgrid[0:l*np.sin(r_theta):1000j,0:6.28:50j]
cx=cr*np.cos(ctheta)
cy=cr*np.sin(ctheta)
cz=np.sqrt(cx**2+cy**2)/np.tan(r_theta)gammar=np.linspace(0,1,100)
theta=np.arctan(np.sin(r_theta)*np.tan(gammar))/np.sin(r_theta)-gammar
R=np.arctan(np.tan(r_theta)/np.cos(gammar ))
x=l*np.sin(R)*np.sin(theta)
y=l*np.sin(R)*np.cos(theta)
z=l*np.cos(R)fig=plt.figure()
fig.suptitle('sperical Involute')ax = Axes3D(fig)ax.plot_surface(cx,cy,cz)
ax.plot(x,y,z)
plt.axis('equal')plt.show()
多元酸水解pH值计算
磷酸二氢钾的水解系数
化简得到的平衡方程:
[H+]^5
+ (k1+c) [H+]^4
+ (k1k2-k) [H+]^3
+ (k1k2k3-(kk1+ck1k2)) [H+]^2
- (kk1k2+2ck1k2k3) [H+]^1
- kk1k2k3 = 0
python求解,有点毛病,python算不出来,后来改用的MATLAB。
from sympy import *x = Symbol('x')k1 = 0.00752
k2 = 0.0000000623
k3 = 0.00000000000022
k = 0.00000000000001
c =0.01
p4=k1+c
p3=k1*k2-k
p2=k1*k2*k3-(k*k1+c*k1*k2)
p1=-(k*k1*k2+2*c*k1*k2*k3)
p0=-k*k1*k2*k3print(p4,p3,p2,p1,p0)
print(solve([x**5+p4*x**4+p3*x**3+p2*x**2+ p1*x+0.1+p0],[x]))