关系数据可视化

article/2025/10/1 3:47:47

关系数据可视化

本文所做的数据的数据可视化实现基于python 3.9.4，需安装matplotlib、numpy、pyecharts、pandas、plotly等依赖库，可通过下述命令完成。

pip install matplotlib
pip install numpy
pip install -v pyecharts==1.1.0
pip install plotly
pip install pandas

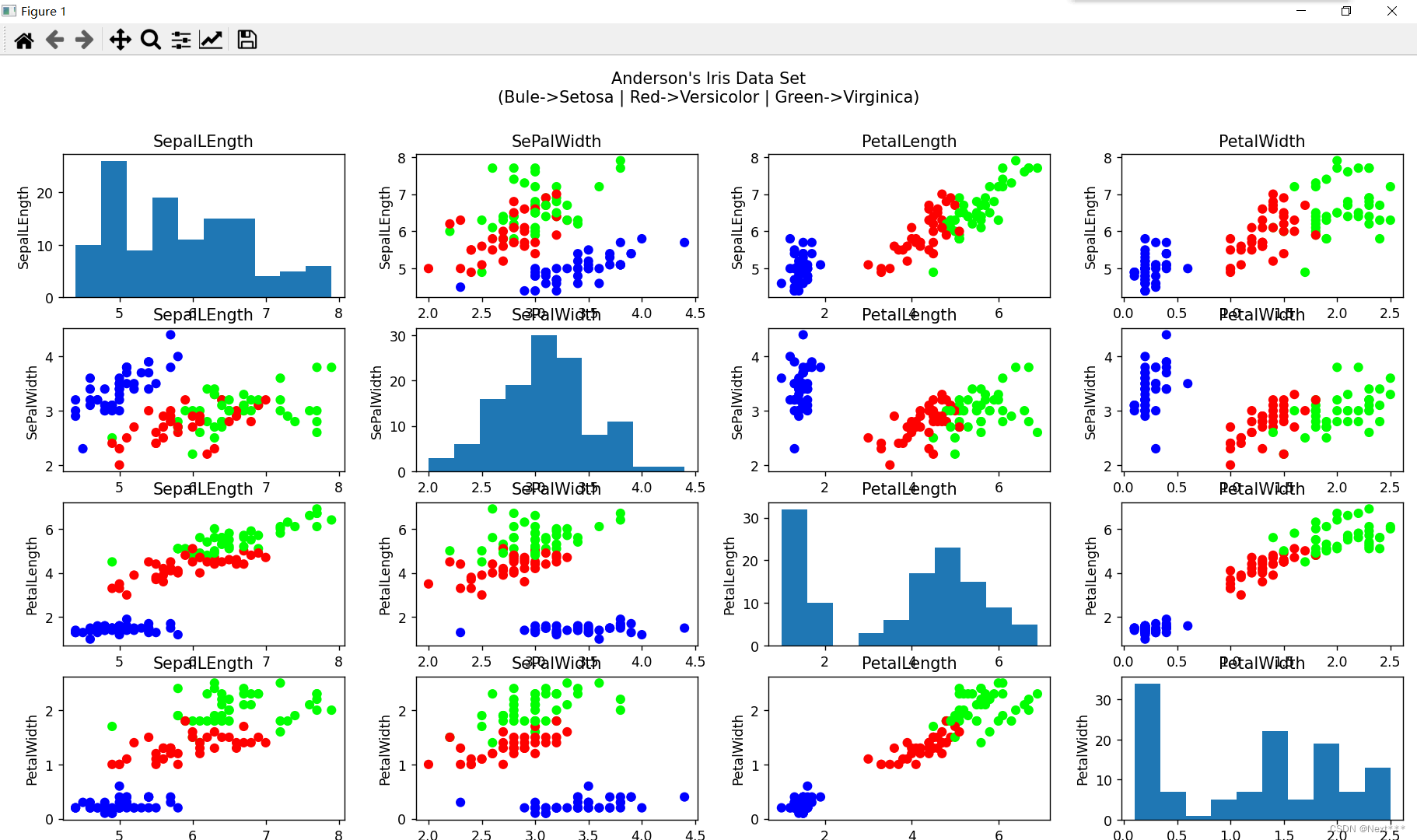
散点图

又称XY散点图，将数据以点的形式展现，显示变量间的相互关系或者影响程度，点的位置由变量的数值决定。

场景：显示若干数据系列中各数值之间的关系，类似XY轴，判断两变量之间是否存在某种关联，或者发现数据的分布或聚合情况

优点：

  • 可以展示数据的分布和聚合情况

  • 适合展示较大的数据集

缺点：

  • 散点图看上去比较乱，基本只能看相关、分布和聚合，其他信息均不能很好展现

类似图表： 气泡图

示例

import numpy as np
import matplotlib.pyplot as plt# Scatter plot
N = 50
x = np.random.rand(N)
y = np.random.rand(N)
colors = np.random.rand(N)
area = (30 * np.random.rand(N))**2  # 0 to 15 point radiiplt.scatter(x, y, s=area, c=colors, alpha=0.5)
plt.title('Scatter plot')
plt.show()# Scatter plot on polar axis
# Compute areas and colors
N = 150
r = 2 * np.random.rand(N)
theta = 2 * np.pi * np.random.rand(N)
area = 200 * r**2
colors = thetafig = plt.figure()
ax = fig.add_subplot(111, projection='polar')
c = ax.scatter(theta, r, c=colors, s=area, cmap='hsv', alpha=0.75)
plt.title('Scatter plot on polar axis')
plt.show()from matplotlib.ticker import NullFormatter
# Scatter plot with histograms
# the random data
N = 1000
x = np.random.randn(N)
y = np.random.randn(N)# no labels
nullfmt = NullFormatter()         # definitions for the axes
left, width = 0.1, 0.65
bottom, height = 0.1, 0.65
bottom_h = left_h = left + width + 0.02rect_scatter = [left, bottom, width, height]
rect_histx = [left, bottom_h, width, 0.2]
rect_histy = [left_h, bottom, 0.2, height]# start with a rectangular Figure
plt.figure(1, figsize=(8, 8))axScatter = plt.axes(rect_scatter)
axHistx = plt.axes(rect_histx)
axHisty = plt.axes(rect_histy)# no labels
axHistx.xaxis.set_major_formatter(nullfmt)
axHisty.yaxis.set_major_formatter(nullfmt)# the scatter plot:
axScatter.scatter(x, y)# now determine nice limits by hand:
binwidth = 0.25
xymax = max(np.max(np.abs(x)), np.max(np.abs(y)))
lim = (int(xymax/binwidth) + 1) * binwidthaxScatter.set_xlim((-lim, lim))
axScatter.set_ylim((-lim, lim))bins = np.arange(-lim, lim + binwidth, binwidth)
axHistx.hist(x, bins=bins)
axHisty.hist(y, bins=bins, orientation='horizontal')axHistx.set_xlim(axScatter.get_xlim())
axHisty.set_ylim(axScatter.get_ylim())plt.title('Scatter plot with histograms')
plt.show()# Scatter Masked
N = 100
r0 = 0.6
x = 0.9 * np.random.rand(N)
y = 0.9 * np.random.rand(N)
area = (20 * np.random.rand(N))**2  # 0 to 10 point radii
c = np.sqrt(area)
r = np.sqrt(x * x + y * y)
area1 = np.ma.masked_where(r < r0, area)
area2 = np.ma.masked_where(r >= r0, area)
plt.scatter(x, y, s=area1, marker='^', c=c)
plt.scatter(x, y, s=area2, marker='o', c=c)
# Show the boundary between the regions:
theta = np.arange(0, np.pi / 2, 0.01)
plt.plot(r0 * np.cos(theta), r0 * np.sin(theta))plt.title('Scatter Masked')
plt.show()# 3D scatter plot
from mpl_toolkits.mplot3d import Axes3D  # noqa: F401 unused importdef randrange(n, vmin, vmax):'''Helper function to make an array of random numbers having shape (n, )with each number distributed Uniform(vmin, vmax).'''return (vmax - vmin)*np.random.rand(n) + vminfig = plt.figure()
ax = fig.add_subplot(111, projection='3d')n = 100# For each set of style and range settings, plot n random points in the box
# defined by x in [23, 32], y in [0, 100], z in [zlow, zhigh].
for c, m, zlow, zhigh in [('r', 'o', -50, -25), ('b', '^', -30, -5)]:xs = randrange(n, 23, 32)ys = randrange(n, 0, 100)zs = randrange(n, zlow, zhigh)ax.scatter(xs, ys, zs, c=c, marker=m)ax.set_xlabel('X Label')
ax.set_ylabel('Y Label')
ax.set_zlabel('Z Label')
plt.title('3D scatter plot')
plt.show()

散点图
极坐标散点图
直方图散点图
分割线散点图

漏斗图

有多个梯形从上到下叠加而成。从上到下的项有逻辑上的顺序关系，梯形面积表示某个环节上业务量与上一个环节的差异。

场景： 适用于业务流程比较规范、周期长、环节多的单流程单项分析，通过漏斗各环节业务数据的比较能够直观地发现和说明问题所在的环节，进而做出决策。

说明：

  • 漏斗图总是开始于一个100%的数量，结束于一个较小的数量；

  • 在开始和结束之间由N个流程环节组成，每个环节用一个梯形来表示；

  • 梯形的上底宽度表示当前环节的输入情况，下底表示当前环节的输出，上底与下底之间的差表现了在当前环节业务量的减小量，当前梯形边的斜率表现了当前环节的减小率；

  • 漏斗图的所有环节的流量都应该使用同一个度量。

类似图表： 金字塔图、对称漏斗图（旋风）、对比漏斗图

示例

from plotly import graph_objects as gofig = go.Figure(go.Funnel(y=[u"喜欢音乐", u"喜欢中国音乐", u"喜欢国风音乐", u"喜欢近现代国风", u"喜欢安九的歌曲"],x=[98367, 83164, 73532, 58172, 32829],textposition="inside",textinfo="value+percent initial",opacity=0.65,marker={"color": ["deepskyblue", "lightsalmon", "tan", "teal", "silver"],"line": {"width": [4, 2, 2, 3, 1, 1],"color": ["wheat", "wheat", "blue", "wheat", "wheat"]}},connector={"line": {"color": "royalblue","dash": "dot","width": 3}})
)
fig.show()fig = go.Figure()
fig.add_trace(go.Funnel(name='广东',y=[u"喜欢音乐", u"喜欢中国音乐", u"喜欢国风音乐", u"喜欢近现代国风", u"喜欢安九的歌曲"],x=[82732, 72635, 62735, 47272, 45262],textinfo="value+percent initial"))fig.add_trace(go.Funnel(name='台湾',orientation="h",y=[u"喜欢音乐", u"喜欢中国音乐", u"喜欢国风音乐", u"喜欢近现代国风", u"喜欢安九的歌曲"],x=[63738, 42826, 41272, 40832, 35262],textposition="inside",textinfo="value+percent previous"))fig.add_trace(go.Funnel(name='云南',orientation="h",y=[u"喜欢音乐", u"喜欢中国音乐", u"喜欢国风音乐", u"喜欢近现代国风", u"喜欢安九的歌曲"],x=[98273, 83736, 76353, 69354, 54362],textposition="outside",textinfo="value+percent total"))fig.show()

漏斗图
多层漏斗图

树图

通过树形结构来展现层级数据的组织关系，以父子层次结构来组织对象，是枚举法的一种表达方式

场景：适用于与组织结构相关的分析，即有明确的层次关系数据

优点：

  • 展现层次关系

  • 可以看到各层级指标间的关系，科进行简单的上卷、下钻等操作

缺点：

  • 数据层级不宜过多

  • 每层的成员不宜过多

  • 无法展现个部分的占比关系

类似图表：矩阵树图

示例

from pyecharts import options as opts
from pyecharts.charts import Treedata = [{"name": "诗歌分类","children": [{"name": "古诗分类","children": [{"name": "按音律分类","children": [{"name": "古体诗", "value": 1000},{"name": "近体诗", "value": 2000},{"name": "词", "value": 3000},{"name": "曲", "value": 4000}]},{"name": "按内容分类","children": [{"name": "叙事诗", "value": 1000},{"name": "抒情诗", "value": 2000},{"name": "送别诗", "value": 3000},{"name": "边塞诗", "value": 4000},{"name": "山水田园诗", "value": 5000},{"name": "咏史诗", "value": 6000},{"name": "咏物诗", "value": 7000},{"name": "悼亡诗", "value": 8000},{"name": "讽喻诗", "value": 9000}]}]},{"name": "新诗分类","children": [{"name": "叙事诗", "value": 1000},{"name": "抒情诗", "value": 2000},{"name": "格律诗", "value": 3000},{"name": "自由诗", "value": 4000},{"name": "散文诗", "value": 5000},{"name": "韵脚诗", "value": 6000},{"name": "现代诗", "value": 7000}]}]
}]c = (Tree().add("诗歌分类",data,collapse_interval=10,# BT: Bottom to top# RL: Right to left# LR: Left to right# TB: Top to buttomorient="TB",# Divergent tree graph# layout="radial",).set_global_opts(title_opts=opts.TitleOpts(title="诗歌分类"))
)
c.render("诗歌分类.html")

树图

矩阵树图

采用矩形表示层次结构的节点，父子层次关系用矩阵间相互嵌套来表达。从根节点开始，空间根据相应的子节点数目被分成多个矩形，矩形的面积大小对应节点的属性，每个矩形又按照相应节点的子节点递归的进行分割，直到叶子节点为止。

场景：适合展现具有层级关系的数据，能够直观体现同级之间的比较

优点：

  • 图形更紧凑，同样大小的画布可以展现更多信息

  • 可以展现成员间的权重

缺点：

  • 不够直观、明确，不像树图那么清晰

  • 分类占比太小时不容易排布

类似图表：树图、马赛克图、热力图

from pyecharts import options as opts
from pyecharts.charts import TreeMapdata = [{"value": 120,"name": "四书","children": [{"value": 30, "name": "大学"},{"value": 40, "name": "中庸"},{"value": 40, "name": "论语"},{"value": 10, "name": "孟子"},],},{"value": 180,"name": "五经","children": [{"value": 30, "name": "礼记"},{"value": 40, "name": "尚书"},{"value": 40, "name": "诗经"},{"value": 25, "name": "周易"},{"value": 45, "name": "春秋"},],},{"value": 240,"name": "六艺","children": [{"value": 30, "name": "礼"},{"value": 40, "name": "乐"},{"value": 50, "name": "射"},{"value": 25, "name": "御"},{"value": 45, "name": "书"},{"value": 50, "name": "数"},],},
]c = (TreeMap().add("四书五经六艺", data).set_global_opts(title_opts=opts.TitleOpts(title="四书五经六艺"))
)
c.render("四书五经六艺.html")

矩阵树图

桑基图

通过页面访问量PV和访客数量UV推算出网页的转化率，进而可以了解网站的整体运营效果和某一类商品的最终成交量

场景： 适用于电商或与营销相关的分析，比如分析购物网站中，哪些商品最畅销或者哪一个时间段是访问高峰

优点：

  • 特别适合分析展现网站流量的运营数据

  • 显示结果直观，可以清晰的看到各个维度指标变化的情况

  • 支持以某个节点查看该节点所在的流程情况

缺点：

  • 应用面窄，只能显示三级维度的流程数据

  • 对显示的度量要求很严格

示例

import pandas as pd
from pyecharts.charts import Sankey
from pyecharts import options as optsdf = pd.DataFrame({'舞蹈类别': ['古典舞', '民族舞', '惊鸿舞', '民族舞', '惊鸿舞', '古典舞', '惊鸿舞'],'舞蹈名称': ['唐宫夜宴', '喜上眉梢', '一舞倾城', '碎梦忧人', '飞雪玉花', '鸿音', '一舞倾城'],'推荐结果': ['未观看', '观看', '观看', '未观看', '未观看', '观看', "未观看"],'观看次数': [937, 732, 837, 635, 1823, 1298, 397]
})nodes = []
for i in range(3):vales = df.iloc[:, i].unique()for value in vales:dic = {}dic['name'] = valuenodes.append(dic)first = df.groupby(['舞蹈类别', '舞蹈名称'])['观看次数'].sum().reset_index()
second = df.iloc[:, 1:]
first.columns = ['source', 'target', 'value']
second.columns = ['source', 'target', 'value']
result = pd.concat([first, second])linkes = []
for i in result.values:dic = {}dic['source'] = i[0]dic['target'] = i[1]dic['value'] = i[2]linkes.append(dic)pic = (Sankey().add('舞蹈推荐分析',nodes,linkes,linestyle_opt=opts.LineStyleOpts(opacity=0.3, curve=0.5, color='source'),label_opts=opts.LabelOpts(position='right'),node_gap=30,#orient="vertical",).set_global_opts(title_opts=opts.TitleOpts(title='舞蹈推荐分析'))
)
pic.render('舞蹈推荐分析.html')

桑基图


http://chatgpt.dhexx.cn/article/T77kTr2d.shtml

相关文章

Echarts数据可视化

Echarts数据可视化

Echarts Echarts 简介Echarts快速上手柱状图柱状图的基本使用其他常见效果 通用配置项titletooltiptoolboxlegend 折线图折线图基本配置其他效果 饼状图 Echarts 简介 Echarts 缩写来自 Enterprise Charts&#xff08;商业级数据图表&#xff09;&#xff0c;是百度的一个开源的…
阅读更多...
实验4 Matplotlib数据可视化

实验4 Matplotlib数据可视化

1. 实验目的 ①掌握Matplotlib绘图基础&#xff1b; ②运用Matplotlib&#xff0c;实现数据集的可视化&#xff1b; ③运用Pandas访问csv数据集。 2. 实验内容 ①绘制散点图、直方图和折线图&#xff0c;对数据进行可视化&#xff1b; ②下载波士顿数房价据集&#xff0c;并…
阅读更多...
数据可视化-期末复习重点笔记

数据可视化-期末复习重点笔记

文章目录 前言一、绘制常见图形。1.1 sinx、cosx曲线图1.2 散点图1.2.1通过matplotlib实现1.2.2通过pyecharts实现 1.3 柱形图1.3.1通过matplotlib实现1.3.2通过pyecharts实现 1.4 柱形堆叠图1.4.1通过matplotlib实现1.4.2通过pyecharts实现 1.5 折线图1.6 拟合曲线1.7 堆叠面积…
阅读更多...
【独家】一文读懂数据可视化

【独家】一文读懂数据可视化

前言 数据可视化，是指将相对晦涩的的数据通过可视的、交互的方式进行展示，从而形象、直观地表达数据蕴含的信息和规律。 早期的数据可视化作为咨询机构、金融企业的专业工具，其应用领域较为单一，应用形态较为保守。步入大数据时代，各行各业对数据的重视程度与日俱增，随之…
阅读更多...
4.2 数据可视化

4.2 数据可视化

一、 数据可视化介绍 1. 概念 数据可视化&#xff1a;是指以 图形、图像、地图、动画 等更为生动、易于理解的方式展现具体数据&#xff0c;诠释数据之间的关系和发展的趋势&#xff0c;以期更好地理解和使用数据。 大数据可视化分析利用支持信息可视化的用户界面以及支持分…
阅读更多...
一图胜千言！这10种可视化技术你必须知道

一图胜千言！这10种可视化技术你必须知道

全文共4549字，预计学习时长9分钟 图片来源：Willian Justen deVasconcellos on Unsplash 相比于浩如烟海的数据表格，大部分人还是更喜欢视觉资料，这一点已不足为奇。也是出于这个原因，人们通常才会在学术论文的前几页加上一张图表，并且清楚地标记上各种注释。 当数据科学家…
阅读更多...
谷歌浏览器输入网址显示该网页无法正常运作

谷歌浏览器输入网址显示该网页无法正常运作

谷歌浏览器 是一款大家喜爱使用的浏览器&#xff0c;它为我们的生活提供了便捷&#xff0c; 可是&#xff0c;不少朋友还不知道怎么解决谷歌浏览器无法打开网页的问题 具体如下&#xff1a; 首先&#xff0c;请大家找到电脑中的“谷歌浏览器”&#xff0c;点击进入主界面&…
阅读更多...
谷歌浏览器无法上网，其他浏览器正常，换chrome搜索引擎

谷歌浏览器无法上网，其他浏览器正常，换chrome搜索引擎

谷歌浏览器无法上网&#xff0c;其他浏览器正常&#xff0c;第一种情况&#xff1a;打开代理设置&#xff0c;开启自动检测设置&#xff0c;重新打卡浏览器 情况二&#xff1a;打开windows注册表&#xff0c;删除配置&#xff0c;重启浏览器不废话&#xff0c;上图 情况三&…
阅读更多...
chrome谷歌浏览器通过小米路由器访问网页一会儿后显示：无法访问Internet

chrome谷歌浏览器通过小米路由器访问网页一会儿后显示：无法访问Internet

近一个月&#xff0c;出现了chrome浏览器国内的网页也没法打开了&#xff0c;使用其他浏览器就能正常使用&#xff0c;比如&#xff1a;Edge。 家里宽带上使用的是小米路由器&#xff0c;用chrome访问网站出现如下截图&#xff1a; 经过网上查找相关资料&#xff0c;结合实践配…
阅读更多...
一招搞定谷歌搜索、谷歌学术无法訪问的问题

一招搞定谷歌搜索、谷歌学术无法訪问的问题

近期，谷歌搜索、谷歌学术“突然”无法訪问了？我百思不得其解啊，禁不住想问一下：前辈们。你们这是要如何？我们写个论文easy吗？怒火燃尽，言归正传，事实上要解决问题也是非常easy的，原理不赘述。直接上菜。下面谨代表个人意见，大仙们有好的方法记得留言共享讨论。谢谢。…
阅读更多...
解决Chrome中打不开Google搜索结果链接

解决Chrome中打不开Google搜索结果链接

由于Google的搜索结果都要经过Google跳转&#xff08;Safari上视乎没有跳转&#xff0c;可以直接进入结果页面&#xff09;&#xff0c;默认跳转使用未加密的HTTP连接&#xff0c;经常被我国GFW拦截&#xff0c;导致无法打开Google搜索结果&#xff01; 解决办法是&#xff0c;…
阅读更多...
关于chrome浏览器地址和不能搜索访问的问题

关于chrome浏览器地址和不能搜索访问的问题

正版的chrome浏览器地址 这里别下载错&#xff0c;我就是重装电脑之后下载chrome浏览器然后发现是盗版本的。正版地址:https://www.google.cn/intl/zh-CN/chrome/ 浏览器默认下载地址最好改为除C盘以外的盘&#xff0c;避免C盘以后爆满&#xff0c;在设置里面改。 不能搜索…
阅读更多...
Google chrome谷歌浏览器，打开后是百度搜索或其他搜索怎么办？

Google chrome谷歌浏览器，打开后是百度搜索或其他搜索怎么办？

如果遇到Google浏览器打开后是百度或者其他浏览器&#xff0c;说明我们在谷歌浏览器的设置有问题&#xff0c;只需要下面简单的操作就可以完成替换。 setting-on start-open a specific page or set of a page,在下面的框中手动敲入www.google.com就欧克了
阅读更多...
搜索引擎突然无法访问问题

搜索引擎突然无法访问问题

1.winR键运行 2.输入 inetcpl.cpl 打开 3.点击上方的高级 点击下面重置 勾选删除个人配置 4.最后重启
阅读更多...
实用技巧：Google 搜索打不开的解决方法【图文教程】

实用技巧：Google 搜索打不开的解决方法【图文教程】

很多人都喜欢用 Google 搜索&#xff0c;但自从 Google 服务器搬离中国大陆后&#xff0c;大陆用户用 Google 搜索时会自动跳转到 google.com.hk&#xff0c;不仅莫名其妙的关键字被过滤&#xff0c;而且经常出现“无法显示此网页”&#xff0c;相当悲催。 大家比较熟悉的解决方…
阅读更多...
股票机械交易系统

股票机械交易系统

最近有一个想法就是开发一个股票机械的交易系统&#xff0c;利用网格法去操作&#xff0c;没有半点人的感情。大家有什么想法可以和我交流&#xff0c;也可以提出您的宝贵意见。
阅读更多...
Python +Echarts +PyQt5设计股票期货自动交易系统 一、软件界面设计

Python +Echarts +PyQt5设计股票期货自动交易系统 一、软件界面设计

效果图： 1、python下 使用Qt Designer创建一个窗体 这里选择创建Main Window窗体 得到可视化可编辑窗体。 2、创建布局 每个界面采用Frame控件进行布局，以方便后期显示与隐藏，整体布局中将左侧与顶部位置空出来用于插入侧边菜单栏和顶栏。
阅读更多...
Python +Echarts +PyQt5设计股票期货自动交易系统 二、软件界面响应（一）

Python +Echarts +PyQt5设计股票期货自动交易系统 二、软件界面响应（一）

Python +Echarts +PyQt5设计股票期货自动交易系统 二、软件界面响应 效果图： 上一章《 Python +Echarts +PyQt5设计股票期货自动交易系统 一、软件界面设计 》中我们进行了基本的界面样式、布局、和基础内容设计，其中布局部分包含了四大模块，即： 1、行情模块 （1）、行…
阅读更多...
金融信息化及交易管理系统（股票交易系统APP）

金融信息化及交易管理系统（股票交易系统APP）

目 录 1 绪 论 1 1.1 选题背景及意义 1 1.2 研究现状 1 1.3 研究主要内容 4 2 需求分析与实施方案 5 2.1 虚拟金融信息化交易系统的功能 5 2.2 可行性分析 5 2.3 系统开发技术 5 2.4 系统开发工具及环境 6 2.5 系统开发方式 7 3 需求分析 8 3.1 系统结构 8 3.2 系统描述 9 3.2.…
阅读更多...
同花顺股票自动交易

同花顺股票自动交易

本文转载自&#xff1a; http://www.cnblogs.com/lovebanyi/archive/2012/01/17/2324997.html 作者&#xff1a;lovebanyi 转载请注明该声明。 由于大部分的券商没有提供交易接口。只对顶级的一些机构或大公司提供接口。所以普通的股民大部分是没有办法享受到一些自动化交易的…
阅读更多...
推荐文章

Copyright @ 2022~2023