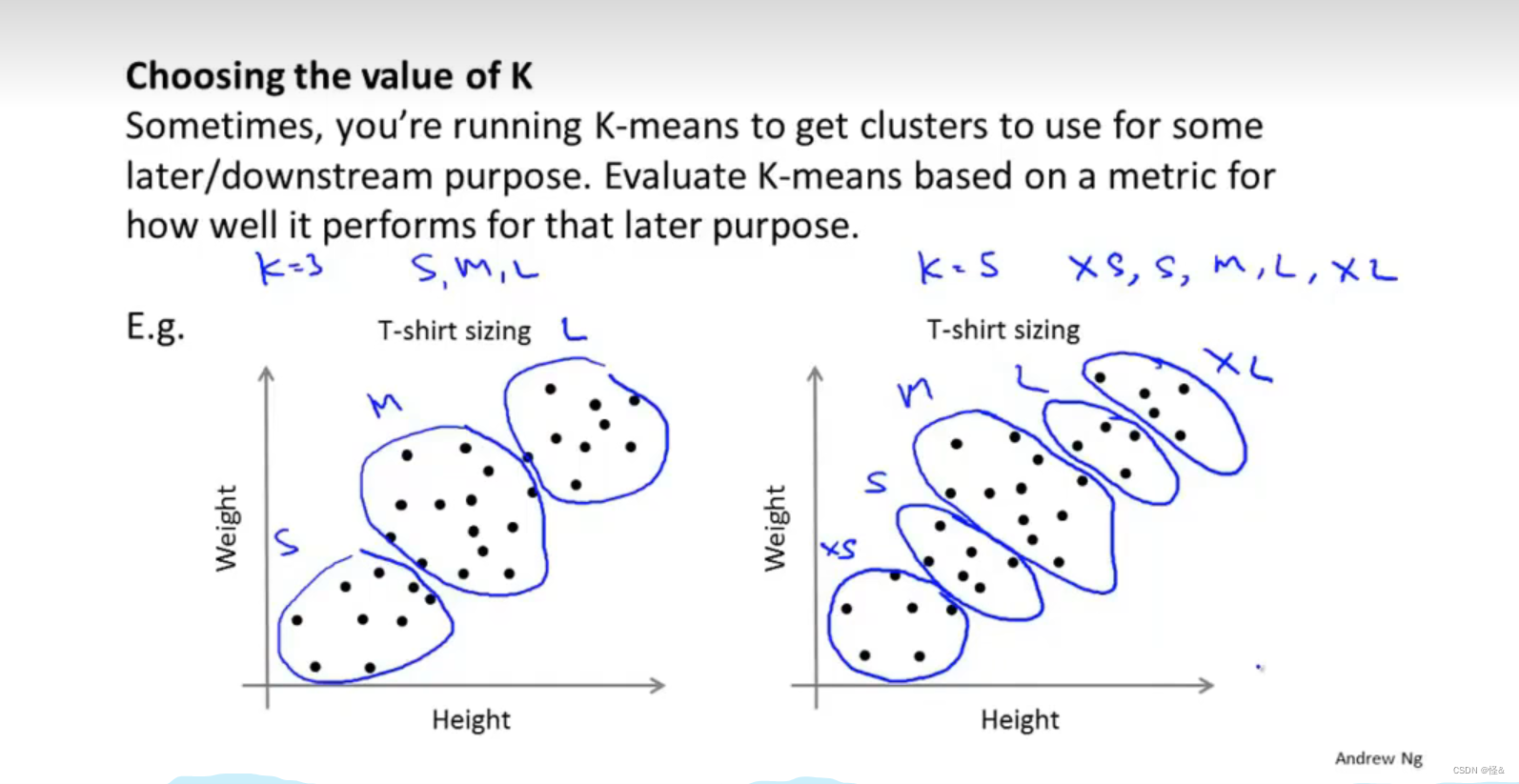
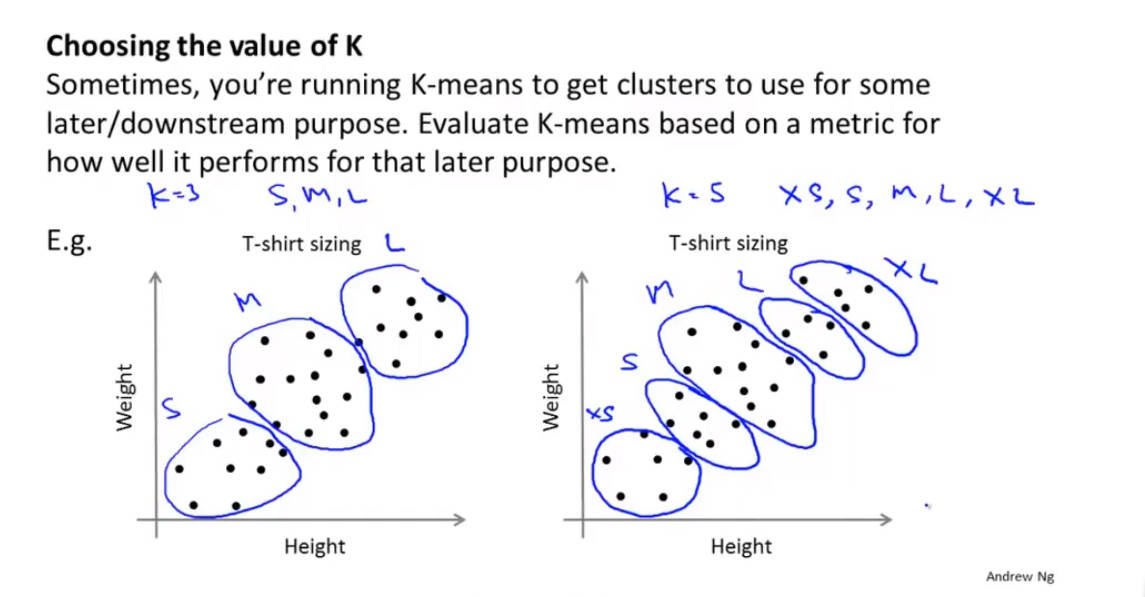
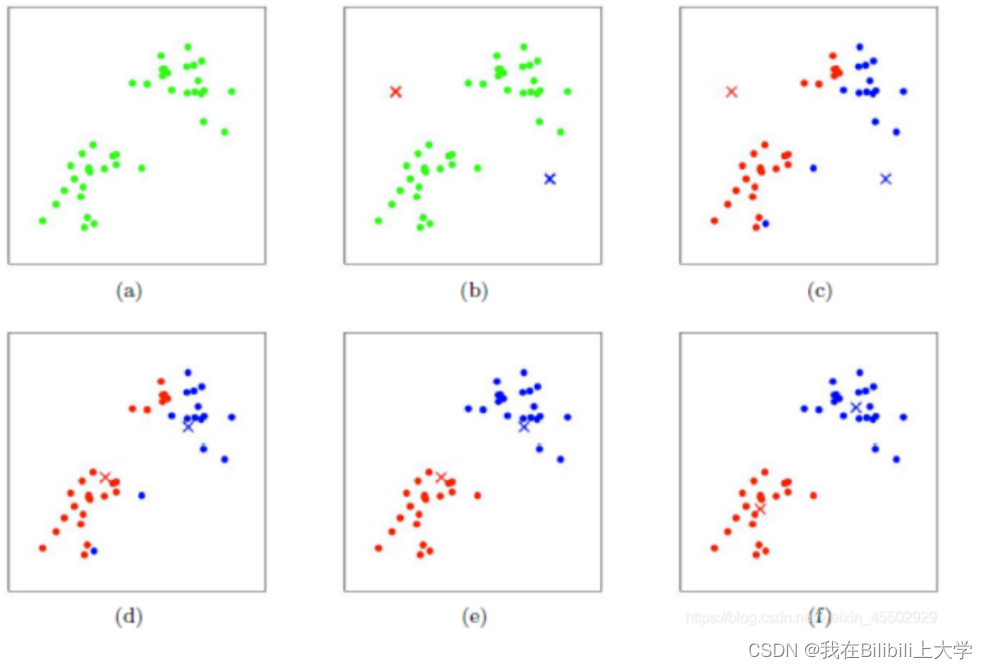
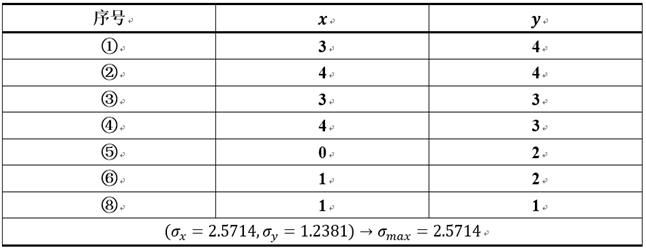
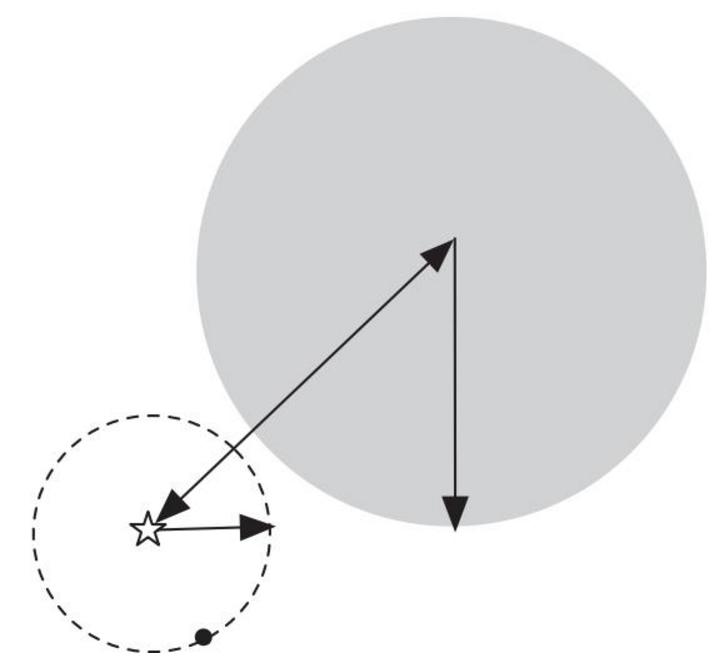
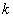学习笔记4-K均值聚类算法

K-均值聚类的一般流程

（1）收集数据：可以使用任何方法收集数据

（2）准备数据：需要数值型数据来计算距离，也可以将标称型数据映射为二值型数据再用于距离计算

（3）分析数据：使用任意方法

（4）训练算法：不适用于无监督学习，即无监督学习没有训练过程

（5）测试算法：应用于聚类算法、观察结果。可以使用量化的误差指标如误差平方和来平均算法的结果

（6）使用算法：可以用于所希望的任何应用。通常情况下，簇质心可以代表整个簇的数据来做出决策

K-均值算法的伪代码

创建k个点作为起始质心（经常是随机选择）

当任意一个点的簇分配结果发生改变时：

对数据集中的每个数据点：

对每个质心：

计算质心与数据点之间的距离：

将数据点分配到距其最近的簇

对每一个簇，计算簇中所有点的均值并将均值作为质心

程序清单10-1 K-均值聚类支持函数

from numpy import *#load data
def loadDataSet(fileName):dataMat = []fr = open(fileName)for line in fr.readlines(): curLine = line.strip().split('\t')fltLine = list(map(float,curLine)) #因为python3中map的返回值变了，所以要加list() 和上章一样修改dataMat.append(fltLine)return dataMat

#计算两个向量的欧式聚类
def distEclud(vecA,vecB):return sqrt(sum(power(vecA - vecB, 2)))  # la.norm(vecA-vecB) 向量AB的欧式距离

#生成簇中心矩阵，每个簇中心向量值是样本每一维的平均值，初始情况下是随机值
def randCent(dataSet,k):#获取数据集中的特征个数n = shape(dataSet)[1]centroids = mat(zeros((k,n)))#遍历数据中的每一维for j in range(n):#计算每一维的最大值和最小值，获得每一维的数据跨度，这样就可以生成数据范围内的随机数minJ = min(dataSet[:,j])rangeJ = float(max(dataSet[:,j])-minJ)#这里注意randint函数中的参数范围一定按大小顺序传入,此处使用random.rand(k,1)函数一定在文件头部写上如下语句#from numpy import *centroids[:,j] = mat(minJ + rangeJ * random.rand(k,1))return centroids

datMat = mat(loadDataSet('Ch10/testSet.txt'))

min(datMat[:,0])

matrix([[-5.379713]])

min(datMat[:,1])

matrix([[-4.232586]])

max(datMat[:,0])

matrix([[ 4.838138]])

max(datMat[:,1])

matrix([[ 5.1904]])

randCent(datMat,2)

matrix([[ 0.44915025,  2.53003187],[-3.05625203,  0.67781452]])

distEclud(datMat[0],datMat[1])

5.184632816681332

程序清单10-2 K-均值聚类算法

#k-均值聚类算法函数，后两个参数为计算两个向量之间的距离函数引用和计算簇中心的函数引用
def kMeans(dataSet,k,disMeas=distEclud,createCent=randCent):#获得样本数量m = shape(dataSet)[0]#定义簇分配结果矩阵，包含两列，一列记录簇索引值，一列记录存储误差值（误差指当前点到簇质心的距离）culsterAssment = mat(zeros((m,2)))#获取簇中心矩阵centroids = createCent(dataSet,k)#簇中心变量是否变化标志clusterChanged = True#迭代次数实现不确定，当簇中心矩阵不再变化时停止迭代while(clusterChanged):clusterChanged = False# 遍历每个样本for i in range(m):# 定义最小距离和最小距离所属的类索引minDist = infminIndex = -1# 遍历所有的簇中心，计算该样本与所有簇中心的距离，比较获得距离最小的簇中心for j in range(k):distJI = disMeas(centroids[j, :], dataSet[i, :])#更新最小距离和最近中心索引if distJI < minDist:minDist = distJIminIndex = j# 如果样本聚类索引不等于计算出的最短距离中心索引，则继续迭代，并更新矩阵值if culsterAssment[i, 0] != minIndex:clusterChanged = TrueculsterAssment[i, :] = minIndex, minDist ** 2# print("centroids:", centroids)#在迭代中，聚类变化，则簇中心变化，需要在每次迭代中更新簇中心            for cent in range(k):#过滤出已经聚类的样本ptsInClust = dataSet[nonzero(culsterAssment[:,0].A==cent)[0]]  #https://blog.csdn.net/xinjieyuan/article/details/81477120 参加该贴，理解上句代码含义centroids[cent,:] = mean(ptsInClust,axis=0)return centroids,culsterAssment

dataMat = mat(loadDataSet('Ch10/testSet.txt'))

mycentroids,clusterAssing = kMeans(dataMat,4)

print(mycentroids)

[[ 2.6265299   3.10868015][ 2.65077367 -2.79019029][-2.46154315  2.78737555][-3.53973889 -2.89384326]]

dataMat1 = dataMat[nonzero(clusterAssing[:,0].A==0)[0]]#此处的0指的是指取第一个索引，看那个索引就知道了
dataMat2 = dataMat[nonzero(clusterAssing[:,0].A==1)[0]]
dataMat3 = dataMat[nonzero(clusterAssing[:,0].A==2)[0]]
dataMat4 = dataMat[nonzero(clusterAssing[:,0].A==3)[0]]import matplotlib.pyplot as plt
fig=plt.figure()
ax1=fig.add_subplot(111)
ax1.scatter(dataMat1[:,0].flatten().A[0],dataMat1[:,1].flatten().A[0],c='m',marker='o')
ax1.scatter(dataMat2[:,0].flatten().A[0],dataMat2[:,1].flatten().A[0],c='r',marker='*')
ax1.scatter(dataMat3[:,0].flatten().A[0],dataMat3[:,1].flatten().A[0],c='g',marker='s')
ax1.scatter(dataMat4[:,0].flatten().A[0],dataMat4[:,1].flatten().A[0],c='y',marker='^')
ax1.scatter(mycentroids[0,0],mycentroids[0,1],c='c',marker='+')
ax1.scatter(mycentroids[1,0],mycentroids[1,1],c='c',marker='+')
ax1.scatter(mycentroids[2,0],mycentroids[2,1],c='c',marker='+')
ax1.scatter(mycentroids[3,0],mycentroids[3,1],c='c',marker='+')
plt.show()

在这里插入图片描述

二分k-means聚类

可以使用SSE(sum of squared error误差平方和)来度量聚类的效果，SSE值越小表示数据点接近于它的质心，聚类效果越好。因为对误差取了平方，因此更加重视那些远离质心的点。

二分k-means聚类算法的思想是先将所有数据点当作一个簇，然后将该簇一分为二。之后在现有的簇中选择一个簇进行划分，选择哪个簇取决于划分哪个簇后能使SSE值最小。不断重复上述过程，直到达到用户要求的簇的个数

二分K-均值算法（bisecting K-means）的伪代码

将所有点看成一个簇

当簇数目小于k时：

对于每个簇：

计算总误差：

在给定的簇上面进行K-均值聚类（k=2）：

计算将该簇一分为二之后的总误差

选择使得误差最小的那个簇进行划分操作

程序清单10-2 二分K-均值聚类算法

def biKmeans(dataSet,k,distMeas=distEclud):#数据集，簇数，计算距离的方法m=shape(dataSet)[0]clusterAssment = mat(zeros((m,2)))#定义簇分配结果矩阵-第1列：簇索引值，第2列：存储误差（点到簇中心的距离）centroid0=mean(dataSet,axis=0).tolist()[0]#初始簇中心--仅1个centList=[centroid0] #创建一个列表--用于存放centroidsfor j in range(m):clusterAssment[j,1]=distMeas(mat(centroid0),dataSet[j,:])**2while (len(centList) < k):  #尝试划分每一簇lowestSSE = inf  #初始化 SSEfor i in range(len(centList)):#对于每一个中心点ptsInCurrCluster = dataSet[nonzero(clusterAssment[:, 0].A == i)[0],:] #筛选当前在第i簇的所有数据点centroidMat, splitClustAss = kMeans(ptsInCurrCluster, 2, distMeas)#将第i个cluster划分，k=2,kMeanssseSplit = sum(splitClustAss[:, 1])#计算第i个cluster的SSE 误差总和sseNotSplit = sum(clusterAssment[nonzero(clusterAssment[:, 0].A != i)[0], 1])# 其他clusters的SSEprint("sseSplit, and notSplit: ", sseSplit, sseNotSplit)# 划分后的误差和没有进行划分的数据集的误差之和为本次误差if (sseSplit + sseNotSplit) < lowestSSE: #判断误差bestCentToSplit = i    #记录应该被划分的中心的索引bestNewCents = centroidMat #最好的新划分出来的中心bestClustAss = splitClustAss.copy()lowestSSE = sseSplit + sseNotSplit  #更新总的误差平方和#更新簇的分配结果bestClustAss[nonzero(bestClustAss[:, 0].A == 1)[0], 0] = len(centList)  #将1改变为新增簇的编号,#cluster i被分为2个clusters,第2个cluster作为新添加的clusterbestClustAss[nonzero(bestClustAss[:, 0].A == 0)[0], 0] = bestCentToSplit    #将0改变为划分簇的编号#第1个cluster仍作为cluster iprint('the bestCentToSplit is: ', bestCentToSplit)#被划分的cluster--第i个clusterprint('the len of bestClustAss is: ', len(bestClustAss))#被划分的cluster i的样本数目#使用新生成的两个质心坐标代替原来的质心坐标centList[bestCentToSplit] = bestNewCents[0, :].tolist()[0]centList.append(bestNewCents[1, :].tolist()[0])#给簇和误差结果矩阵重新赋值clusterAssment[nonzero(clusterAssment[:, 0].A == bestCentToSplit)[0],:] = bestClustAss#用新的聚类结果替换原来的return mat(centList), clusterAssment #返回：簇中心，簇分配结果

datMat3 = mat(loadDataSet('Ch10/testSet2.txt'))

centList,myNewAssments = biKmeans(datMat3,3)

sseSplit, and notSplit:  453.033489581 0.0
the bestCentToSplit is:  0
the len of bestClustAss is:  60
sseSplit, and notSplit:  77.5922493178 29.1572494441
sseSplit, and notSplit:  12.7532631369 423.876240137
the bestCentToSplit is:  0
the len of bestClustAss is:  40

def plotKMeans(dataSet, clusterAssment, cenroids):"""函数说明：绘制聚类后情况:param dataSet: 数据集:param clusterAssment: 聚类结果:param cenroids: 质心坐标:return:"""m = shape(dataSet)[0]x0 = dataSet[nonzero(clusterAssment[:, 0] == 0), 0][0].tolist()y0 = dataSet[nonzero(clusterAssment[:, 0] == 0), 1][0].tolist()x1 = dataSet[nonzero(clusterAssment[:, 0] == 1), 0][0].tolist()y1 = dataSet[nonzero(clusterAssment[:, 0] == 1), 1][0].tolist()x2 = dataSet[nonzero(clusterAssment[:, 0] == 2), 0][0].tolist()y2 = dataSet[nonzero(clusterAssment[:, 0] == 2), 1][0].tolist()x3 = dataSet[nonzero(clusterAssment[:, 0] == 3), 0][0].tolist()y3 = dataSet[nonzero(clusterAssment[:, 0] == 3), 1][0].tolist()plt.scatter(x0, y0, color = 'red', marker='*')plt.scatter(x1, y1, color = 'yellow', marker='o')plt.scatter(x2, y2, color = 'blue', marker='s')plt.scatter(x3, y3, color = 'green', marker='^')for i in range(shape(cenroids)[0]):plt.scatter(cenroids[i, 0], cenroids[i, 1], color='k', marker='+', s=200)plt.show()

print("step 3: show the result...")
plotKMeans(datMat3,myNewAssments,centList)
print('the error of biKmeans:', sum(myNewAssments[:, 1]))

step 3: show the result...

在这里插入图片描述

the error of biKmeans: 106.749498762

import numpy as np
from math import radians, cos, sin, asin, sqrt
import matplotlib.pyplot as pltdef distSLC(vecA, vecB):'''函数说明：计算根据经纬度计算两点之间的距离:param vecA: 一个点坐标向量:param vecB: 另一个点坐标向量:return: 距离'''a = sin(vecA[0,1] * np.pi/180) * sin(vecB[0,1] * np.pi/180)b = cos(vecA[0,1]* np.pi/180) * cos(vecB[0,1]* np.pi/180) * cos(np.pi * (vecB[0,0]-vecA[0,0]) /180)return np.arccos(a + b)*6371.0

def clusterClubs(numClust = 5):"""函数说明：对地图坐标进行聚类，并在地图图片上显示聚类结果:param numClust: 聚类数目:return:"""clubsCoordinate = []fr = open('Ch10/places.txt')for line in fr.readlines():lineCur = line.strip().split('\t')# lineMat = np.mat(lineCur)[0, -2:]   #获取最后两列经纬度# fltLinr = map(float, lineMat.tolist()[0])# clubsCoordinate.append(list(fltLinr))clubsCoordinate.append([float(lineCur[-1]), float(lineCur[-2])])    #获取最后两列经纬度clubsCoordinateMat = np.mat(clubsCoordinate)cenroids, clusterAssment = biKmeans(clubsCoordinateMat, numClust,distMeas=distSLC)plotKMeans(clubsCoordinateMat, clusterAssment, cenroids)fig = plt.figure()rect = [0.1, 0.1, 0.8, 0.8] #使用矩阵来设置图片占绘制面板的位置，左下角0.1,0.1,右上角0.8,0.8scatterMarkers = ['s', 'o', '^', '8', 'p', 'd', 'v', 'h', '>', '<'] #形状列表axprops = dict(xticks=[], yticks=[])ax0 = fig.add_axes(rect, label='ax0', **axprops)imgP = plt.imread('Ch10/Portland.png')   #基于一幅图像来创建矩阵ax0.imshow(imgP)    #绘制该矩阵ax1 = fig.add_axes(rect, label='ax1', frameon=False)for i in range(numClust):ptsInCurrCluster = clubsCoordinateMat[np.nonzero(clusterAssment[:, 0].A == i)[0], :]markerStyle = scatterMarkers[i % len(scatterMarkers)]ax1.scatter(ptsInCurrCluster[:, 0].flatten().A[0], ptsInCurrCluster[:, 1].flatten().A[0], marker=markerStyle,s=90) #flatten()将m*n的矩阵转化为1*(m×n)的矩阵,.A[0]矩阵转化为数组后获取数组第一维数据ax1.scatter(cenroids[:, 0].flatten().A[0], cenroids[:, 1].flatten().A[0], marker='+', s=300)print(sum(clusterAssment[:,1]))plt.show()

clusterClubs()

sseSplit, and notSplit:  3073.83037159 0.0
the bestCentToSplit is:  0
the len of bestClustAss is:  69
sseSplit, and notSplit:  1049.90192822 1388.79984556
sseSplit, and notSplit:  3818.38240361E:\Anaconda3\lib\site-packages\numpy\matrixlib\defmatrix.py:549: RuntimeWarning: Mean of empty slice.return N.ndarray.mean(self, axis, dtype, out, keepdims=True)._collapse(axis)
E:\Anaconda3\lib\site-packages\numpy\core\_methods.py:73: RuntimeWarning: invalid value encountered in true_divideret, rcount, out=ret, casting='unsafe', subok=False)1685.03052602
the bestCentToSplit is:  0
the len of bestClustAss is:  32
sseSplit, and notSplit:  48.1802401926 2238.74422706
sseSplit, and notSplit:  979.633985283 1049.90192822
sseSplit, and notSplit:  307.448480884 1588.75739229
the bestCentToSplit is:  2
the len of bestClustAss is:  25
sseSplit, and notSplit:  48.1802401926 1696.24832645
sseSplit, and notSplit:  1002.31501283 507.406027612
sseSplit, and notSplit:  24.9658774756 1823.25729307
sseSplit, and notSplit:  117.645985825 1661.7059724
the bestCentToSplit is:  1
the len of bestClustAss is:  37

在这里插入图片描述