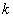🌵🌵🌵前言

✨你好啊，我是“ 怪& ”，是一名在校大学生哦。
🌍主页链接：怪&的个人博客主页
☀️博文主更方向为：课程学习知识、作业题解、期末备考。随着专业的深入会越来越广哦…一起期待。
❤️一个“不想让我曾没有做好的也成为你的遗憾”的博主。
💪很高兴与你相遇，一起加油！

一、应用

市场分割，社交网络分析，组织计算机集群（更好的组织数据集），银河系构成

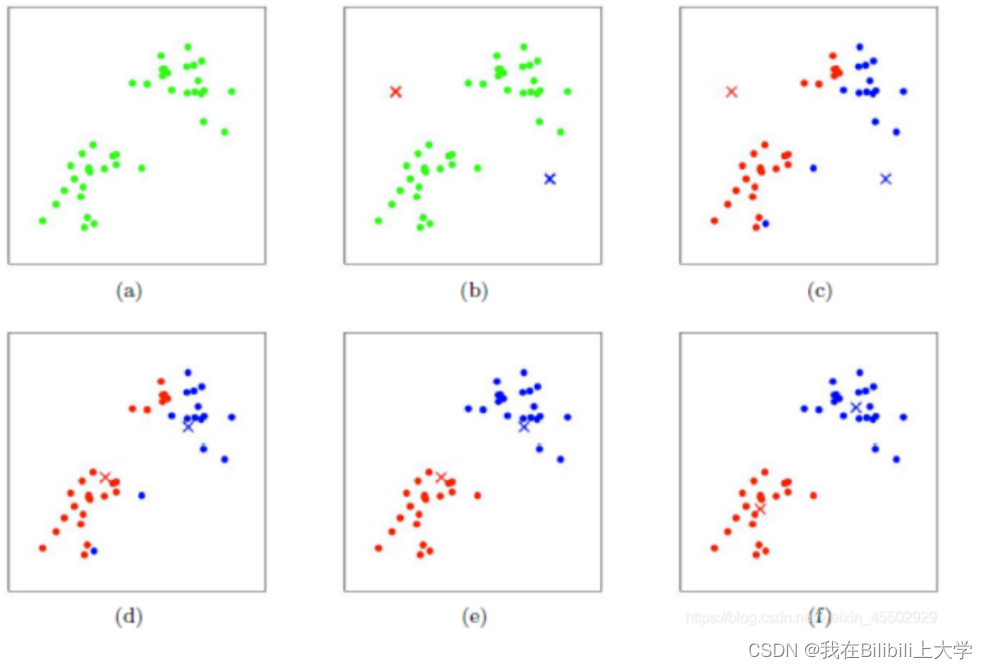
二、k-means

如果遇到没有点的簇中心，则随机初始化

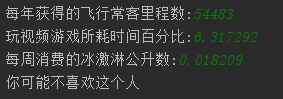
1、参数：

2、过程

3、应用

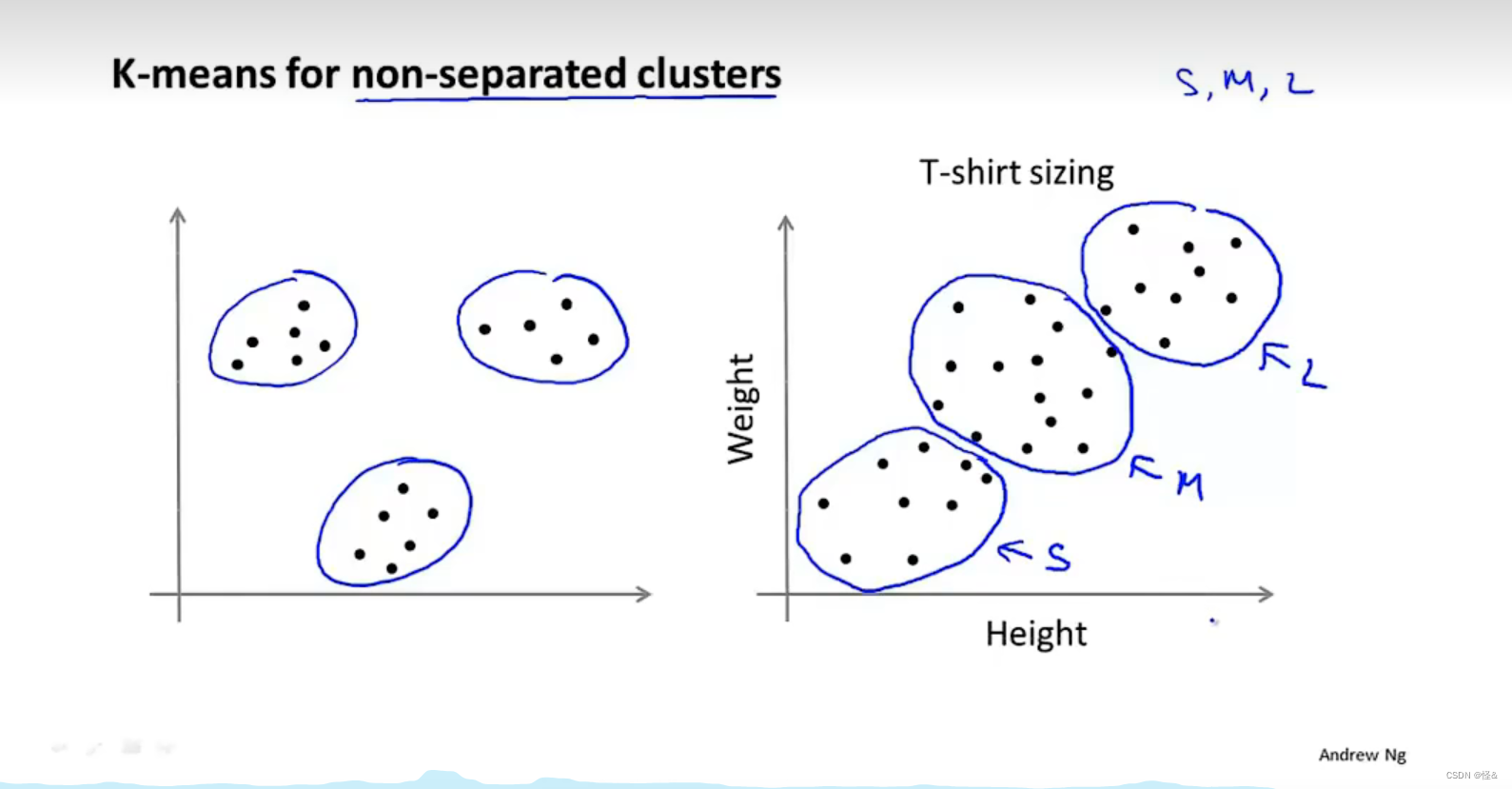
4、优化目标

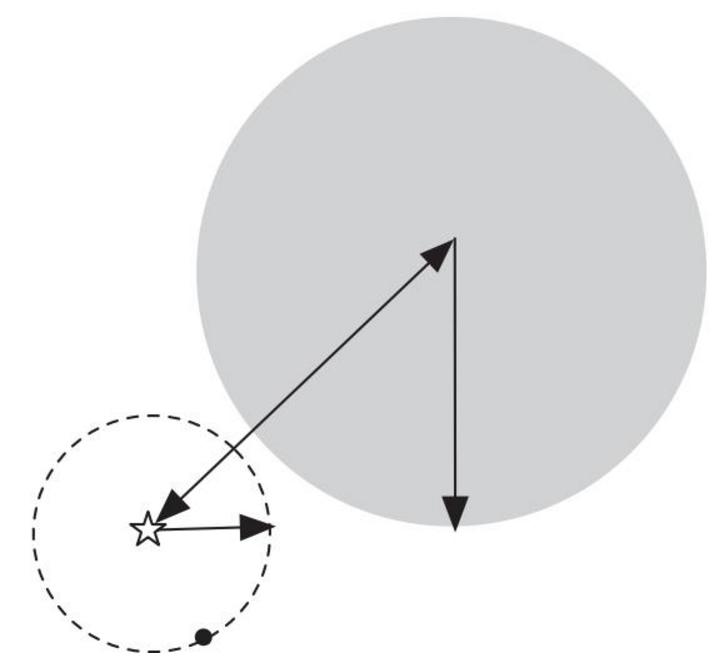
迭代思想，代价函数J也叫失真函数

两部分：
最小化J关于c的变量（找该点距离最小的簇中心）
最小化J关于u的变量
然后保持迭代

5、随机初始化

避免局部最优

k均值算法可能会收敛至不同的结果，这取决于聚类的初始化状态

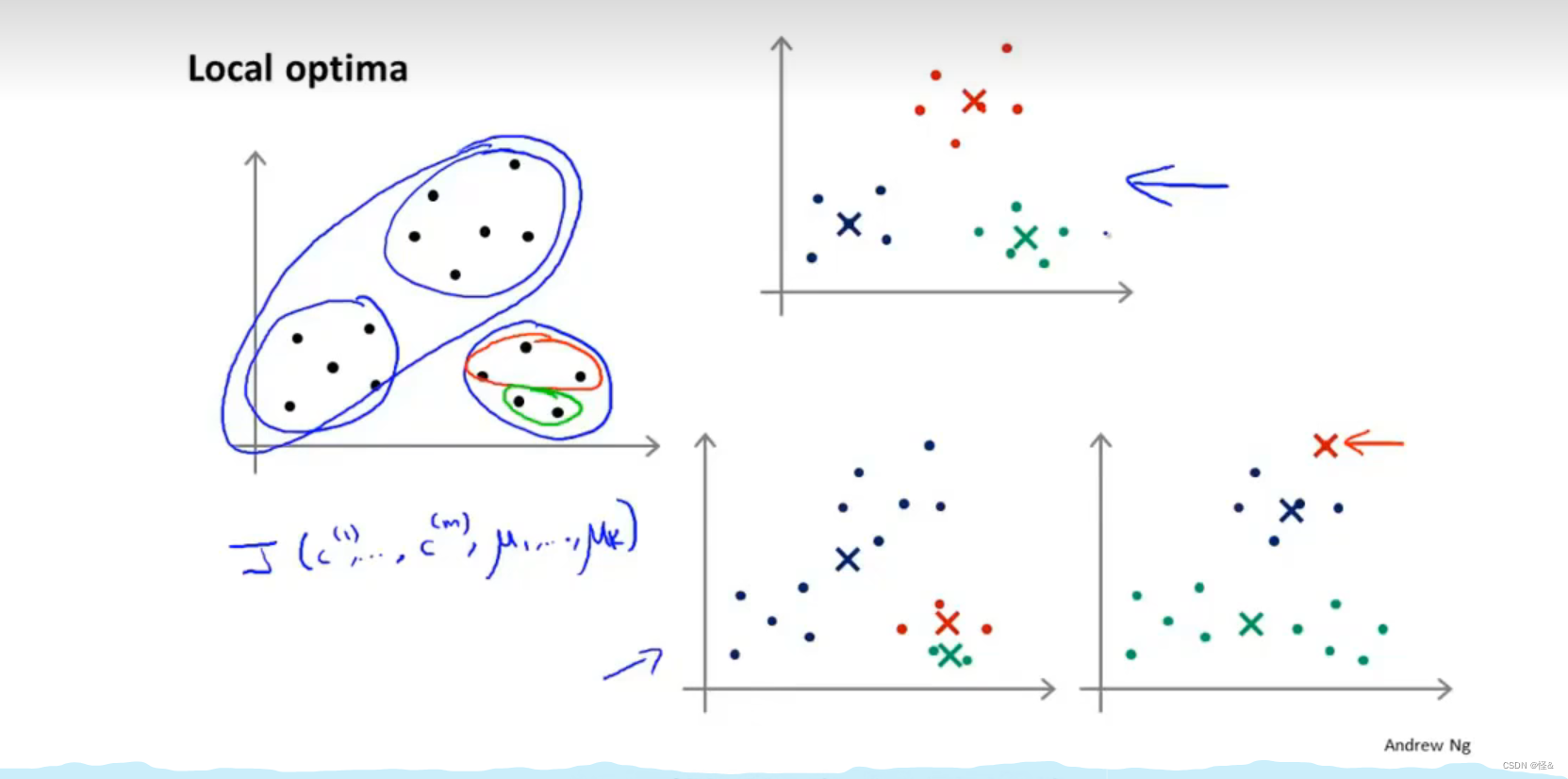
初始化不好，会陷入局部最优（畸变函数J落入局部最优）：
可以初始化k均值算法多次并运行，以此来确保我们最终能得到一个足够好的结果(尽可能好的局部最优和全局最优)

聚类相对较少时，2/3/4，随机初始化有较大的影响，可以很好的最小化畸变函数

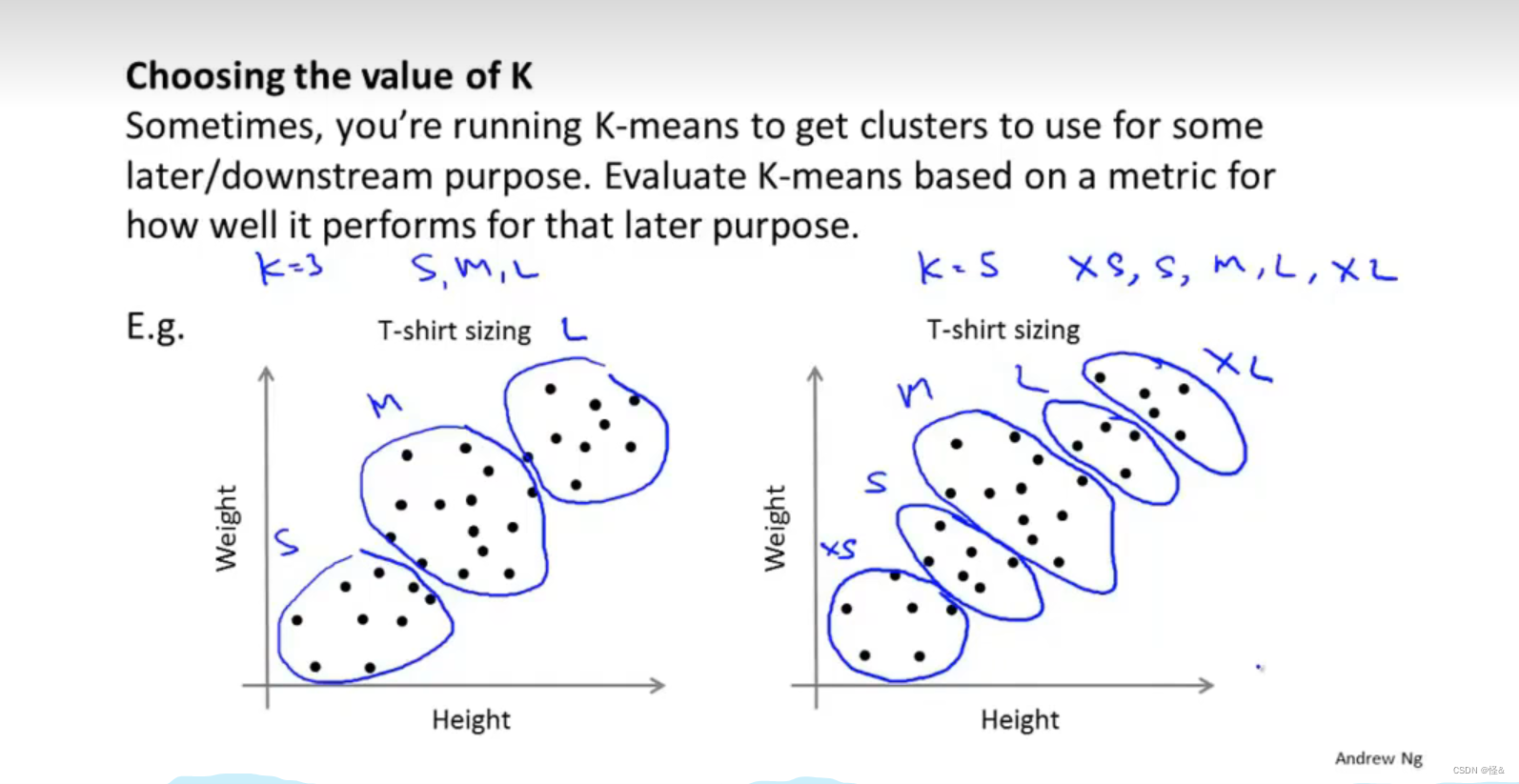
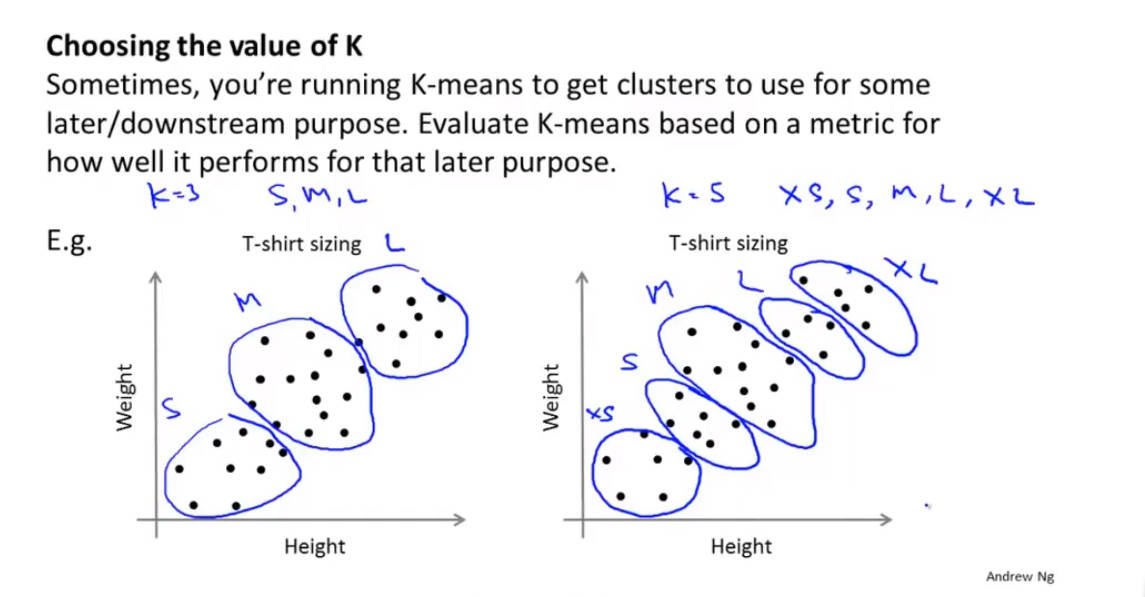
6、聚类数量的选择

1、通过观察可视化的图
2、观察聚类算法的输出

肘部法则：可很好的解决部分问题，例如左图

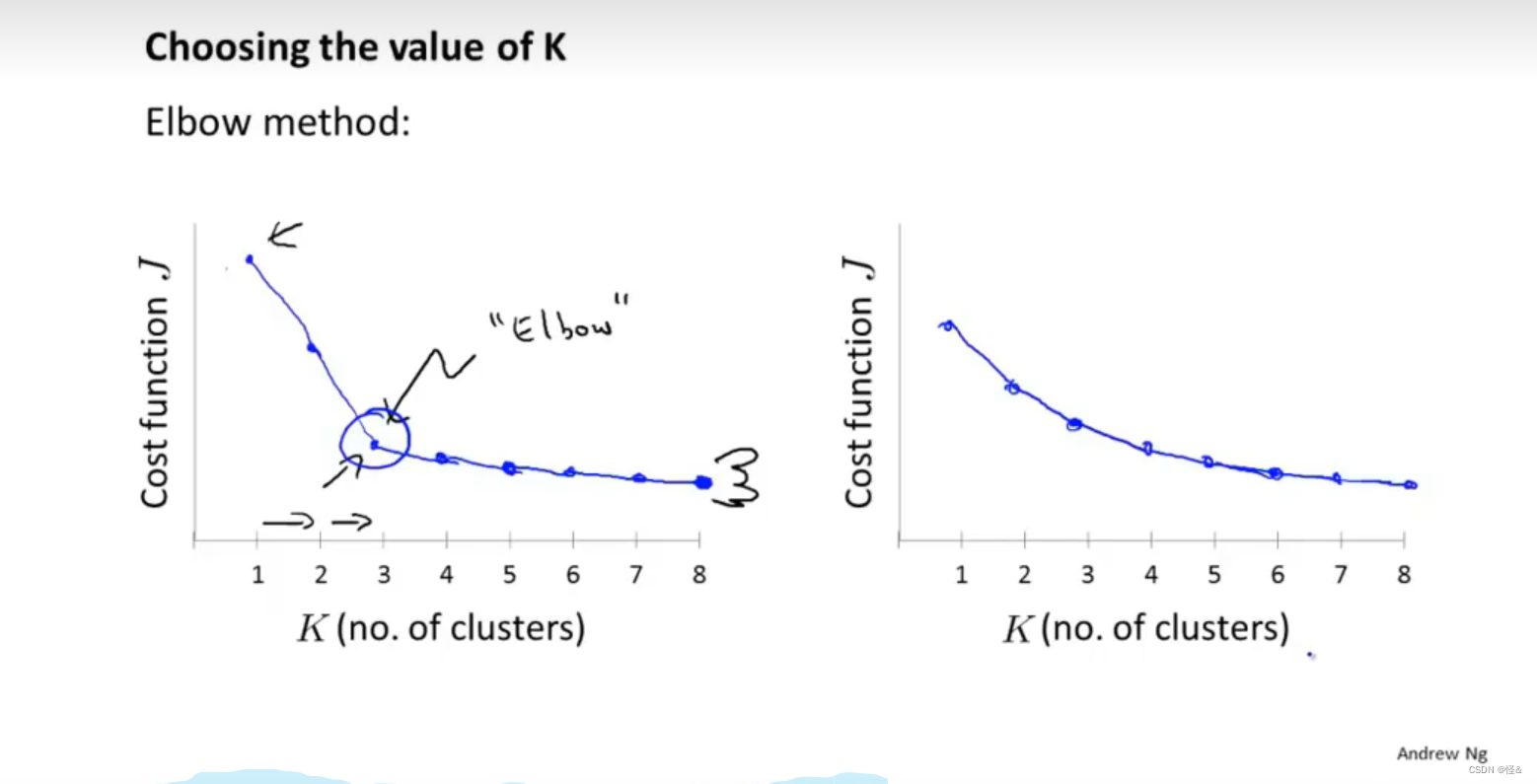
从实际需求出发（后续的下游目的）：运行此k-means算法的目的

❤️❤️❤️忙碌的敲代码也不要忘了浪漫鸭！