数据结构–汉罗塔

题目描述

在经典汉诺塔问题中，有 3 根柱子及 N 个不同大小的穿孔圆盘，盘子可以滑入任意一根柱子。一开始，所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
1.一次只能移动一个圆盘.
2.每个步骤都包括从一座塔中取出上部圆盘并将其放在另一座塔的顶部或空的柱子上.
3.不能将较大的圆盘放置在较小的圆盘上.

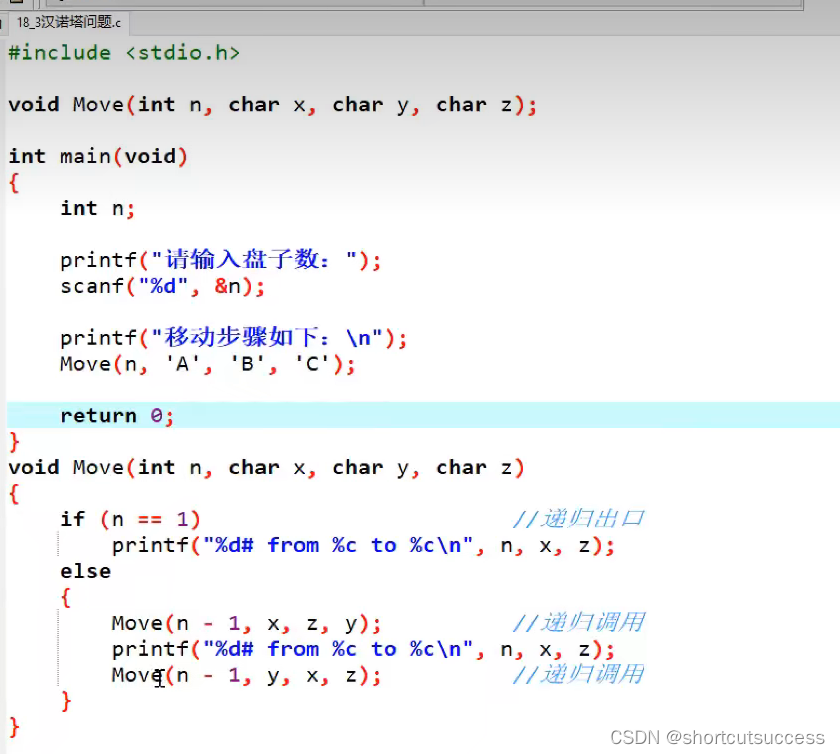
先上代码：

#include <stdio.h>void hanoi(int paraN, char paraSource, char paraDestination, char paraTransit) {printf("paraN is %d, paraN address is %d, paraSource address is %d,paraDestination address is %d, paraTransit address is %d\r\n",paraN, &paraN, &paraSource, &paraDestination, &paraTransit);//打印此时汉罗塔盘子的个数以及和各个柱子的地址if (paraN <= 0) {return;} else {hanoi(paraN - 1, paraSource, paraTransit, paraDestination);printf("%c -> %c \r\n", paraSource, paraTransit);hanoi(paraN - 1, paraDestination, paraSource, paraTransit);}
}void hanoiTest() {printf("---- addToTest begins. ----\r\n");printf("2 plates\r\n");hanoi(2, 'A', 'B', 'C');printf("3 plates\r\n");hanoi(3, 'A', 'B', 'C');printf("---- addToTest ends. ----\r\n");
}int main() {hanoiTest();
}

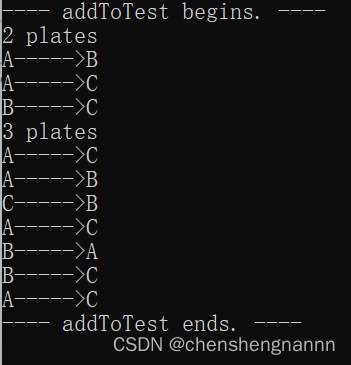
运行结果：

D:\study.clion\untitled7\cmake-build-debug\untitled7.exe
---- addToTest begins. ----
2 plates
paraN is 2, paraN address is 6421968, paraSource address is 6421976,paraDestination address is 6421984, paraTransit addr
ess is 6421992
paraN is 1, paraN address is 6421904, paraSource address is 6421912,paraDestination address is 6421920, paraTransit addr
ess is 6421928
paraN is 0, paraN address is 6421840, paraSource address is 6421848,paraDestination address is 6421856, paraTransit addr
ess is 6421864
A -> B
paraN is 0, paraN address is 6421840, paraSource address is 6421848,paraDestination address is 6421856, paraTransit addr
ess is 6421864
A -> C
paraN is 1, paraN address is 6421904, paraSource address is 6421912,paraDestination address is 6421920, paraTransit addr
ess is 6421928
paraN is 0, paraN address is 6421840, paraSource address is 6421848,paraDestination address is 6421856, paraTransit addr
ess is 6421864
B -> C
paraN is 0, paraN address is 6421840, paraSource address is 6421848,paraDestination address is 6421856, paraTransit addr
ess is 6421864
3 plates
paraN is 3, paraN address is 6421968, paraSource address is 6421976,paraDestination address is 6421984, paraTransit addr
ess is 6421992
paraN is 2, paraN address is 6421904, paraSource address is 6421912,paraDestination address is 6421920, paraTransit addr
ess is 6421928
paraN is 1, paraN address is 6421840, paraSource address is 6421848,paraDestination address is 6421856, paraTransit addr
ess is 6421864
paraN is 0, paraN address is 6421776, paraSource address is 6421784,paraDestination address is 6421792, paraTransit addr
ess is 6421800
A -> C
paraN is 0, paraN address is 6421776, paraSource address is 6421784,paraDestination address is 6421792, paraTransit addr
ess is 6421800
A -> B
paraN is 1, paraN address is 6421840, paraSource address is 6421848,paraDestination address is 6421856, paraTransit addr
ess is 6421864
paraN is 0, paraN address is 6421776, paraSource address is 6421784,paraDestination address is 6421792, paraTransit addr
ess is 6421800
C -> B
paraN is 0, paraN address is 6421776, paraSource address is 6421784,paraDestination address is 6421792, paraTransit addr
ess is 6421800
A -> C
paraN is 2, paraN address is 6421904, paraSource address is 6421912,paraDestination address is 6421920, paraTransit addr
ess is 6421928
paraN is 1, paraN address is 6421840, paraSource address is 6421848,paraDestination address is 6421856, paraTransit addr
ess is 6421864
paraN is 0, paraN address is 6421776, paraSource address is 6421784,paraDestination address is 6421792, paraTransit addr
ess is 6421800
B -> A
paraN is 0, paraN address is 6421776, paraSource address is 6421784,paraDestination address is 6421792, paraTransit addr
ess is 6421800
B -> C
paraN is 1, paraN address is 6421840, paraSource address is 6421848,paraDestination address is 6421856, paraTransit addr
ess is 6421864
paraN is 0, paraN address is 6421776, paraSource address is 6421784,paraDestination address is 6421792, paraTransit addr
ess is 6421800
A -> C
paraN is 0, paraN address is 6421776, paraSource address is 6421784,paraDestination address is 6421792, paraTransit addr
ess is 6421800
---- addToTest ends. ----进程已结束,退出代码0

分析

以下分为七个部分

1.自顶向下，逐渐求精：

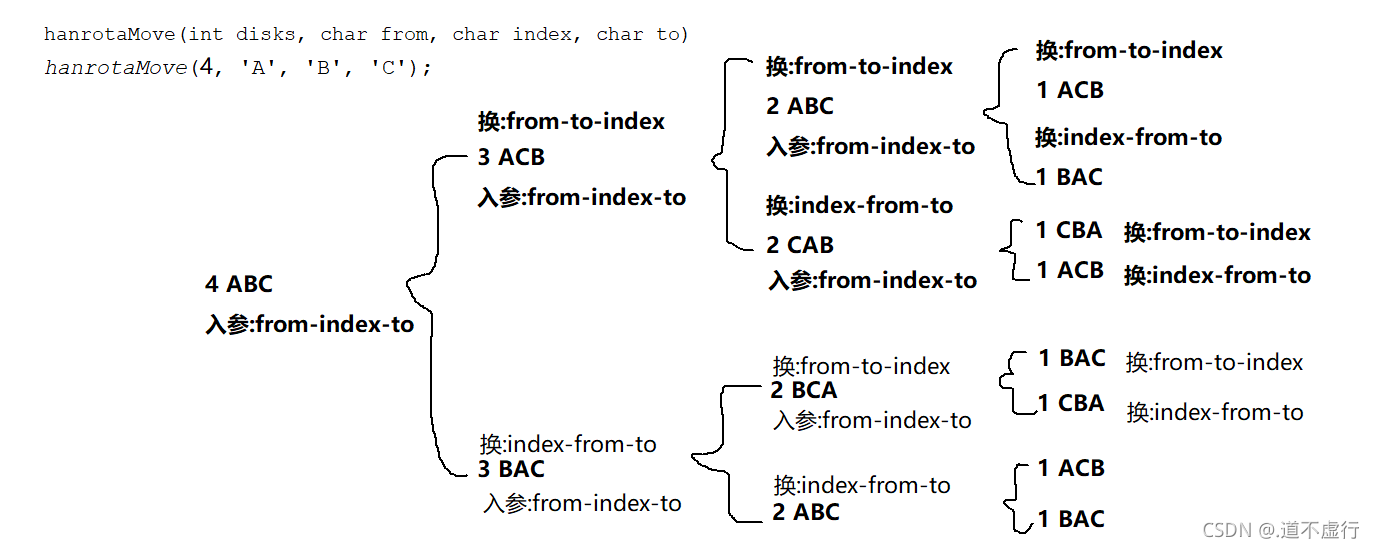
​ 汉罗塔问题的求解方式为自顶向下，逐渐求精。也就是说，若现在有n个盘子，要将这n个盘子从a柱子移动到c柱子，那么我们就可以先把n-1个盘子从a柱子移动到b柱子，然后将第n个柱子移动到c柱子，最后再将那n-1个柱子从b’柱子移动到c柱子上。对于那n-1个盘子，则需要将n-2个盘子从a柱子移动c柱子，再将第n-1个盘子从a柱子移动到b柱子，最后再将那n-2个盘子从c柱子移动到b柱子上…以此类推，可以看出，这里有三个子问题，这三个子问题的思路一致，所以可以用递归来解决。

2.函数调用、递归与分治：

为了解决汉罗塔问题，在上述我们也说了，需要用到递归的方法。具体点说，我们需要编写一个函数，就是上面代码中的void hanoi(int paraN, char paraSource, char paraDestination, char paraTransit)；函数。其中paraN表示要移动的圆盘个数，后面三个分别 表示a,b,c柱子。

3.形参与实参：

在函数调用过程中，我们使用形参来表示函数的输入参数，而实参则是在函数调用时提供的具体数值。在汉诺塔问题中，形参 paraN、paraSource、paraDestination和 paraTransit分别表示要移动的圆盘数和三个柱子。在函数调用时，我们需要提供实际的圆盘数和三个柱子的具体名称，如 void hanoi(int paraN, char paraSource, char paraDestination, char paraTransit)。

4.有意义、规范的标识符：

在编写程序时，使用有意义、规范的标识符可以使代码更易于理解和维护。也就是命名规范。

5.时间复杂度：

汉诺塔问题的时间复杂度为 O(2^n)。n表示有n个盘子。

    if (paraN <= 0) {return;} else {hanoi(paraN - 1, paraSource, paraTransit, paraDestination);printf("%c -> %c \r\n", paraSource, paraTransit);hanoi(paraN - 1, paraDestination, paraSource, paraTransit);}

设盘子个数为n时，需要T（n)步，把A柱子n-1个盘子移到B柱子，需要T（n-1)步，A柱子最后一个盘子移到C柱子一步，B柱子上n-1个盘子移到C柱子上T（n-1)步。
得递推公式T（n）=2T（n-1)+1
所以汉诺塔问题的时间复杂度为O(2^n);

6.递归栈：

递归函数的调用过程需要使用递归栈来保存每个函数调用的状态。在汉诺塔问题中，每个递归调用会创建一个新的函数调用帧，并将其压入递归栈中。当递归调用返回时，对应的函数调用帧会被弹出，恢复到上一层调用的状态。因此，在解决汉诺塔问题的过程中，递归栈的深度等于递归调用的层数，即 n。

7.空间复杂度：

汉诺塔问题的空间复杂度为 O(n)，其中 n 是圆盘的数量。

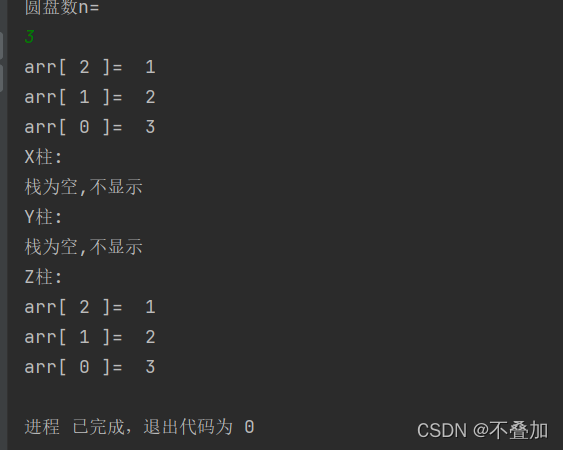
接下来我会以三个盘子为例来讲解。我们把实现汉罗塔的代码单独拿出来说

第一步：我们要先将a柱子上的前两个移动到b柱子上

第二步：我们将a柱子上第三个盘子移动到c柱子上

第三步：将b柱子上的两个盘子移动到c柱子上

当然 我相信伙伴们应该想不明白上面两个盘子怎么移。其实和上述一样。现在我们单独来看前两个盘子，因为第三个盘子是最大的，所以移动前两个盘子的时候不必考虑盘子的大小。在移动前两个盘子的时候，也是要先将第一个盘子先移到c柱子上，然后再将第二个盘子移动到b柱子上，最后再将第一个盘子从c柱子移到b柱子。这样一看是不是和上面的步骤大体一致？所以我们可以写成递归的形式。

无论多少个盘子，就像是n个，都是先将n-1个盘子先从a柱子移动到b柱子，再将第n个盘子移动到c柱子，最后将这n-1个盘子从b柱子移动到c柱子。这样就完成了盘子的移动。

hanoi(paraN - 1, paraSource, paraTransit, paraDestination);
printf("%c -> %c \r\n", paraSource, paraDestination);
hanoi(paraN - 1, paraTransit, paraDestination, paraSource);

所以小伙伴们应该可以理解这三句代码了。

注意:

用递归就一定要有退出条件。在这里，递归的退出条件就是paraN=0。当paraN=0时，就没有盘子在上面了，当然也就没有办法移动了。