一、参考链接：

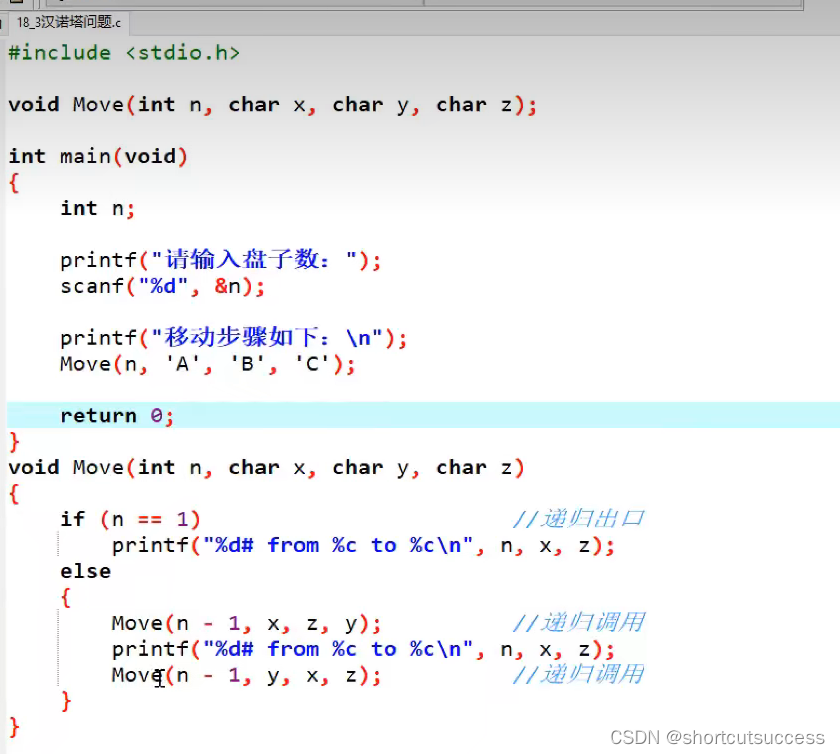
1、普通汉罗塔链接（这边也是我的博文）：

(166条消息) 递归经典算法案例题（汉罗塔、阶乘、斐波那契代码）_南风~古草的博客-CSDN博客_汉罗塔


 

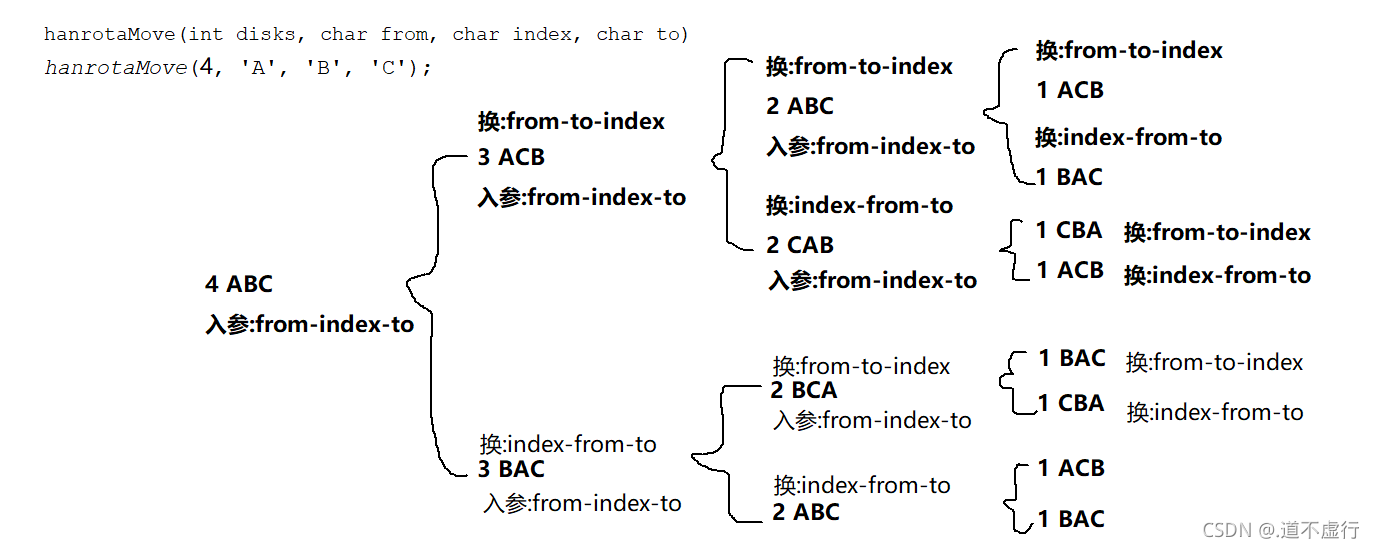
2、大佬的多柱汉罗塔博文（有数学推导，该代码为C++，我这篇python多柱是根据其C++该写过来，思想纯借鉴，plus的地方为个人理解的注释）

(166条消息) 多柱汉诺塔问题浅析——算法及公式推导_li-ucas的博客-CSDN博客_多柱汉诺塔

二、具体题目： 

经典的汉诺塔问题。汉诺塔来源于印度传说的一个故事，上帝创造世界时作了三根金刚石柱子，在一根柱子上从下往上按大小顺序摞着64片黄金圆盘。上帝命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一回只能移动一个圆盘。有预言说，这件事完成时宇宙会在一瞬间闪电式毁灭。也有人相信婆罗门至今仍在一刻不停地搬动着圆盘。恩，当然这个传说并不可信，如今汉诺塔更多的是作为一个玩具存在。有一天你就收到了一个汉诺塔玩具作为生日礼物。 你是个怕麻烦的人，显然将64个圆盘逐一搬动直到所有的盘子都到达第三个柱子上很困难，所以你决定作个小弊，找来了m根一模一样的柱子，通过这m个柱子来更快的把所有的盘子移到第三个柱子上，移动规则一样。 问题：在一次游戏中，使用了n个圆盘时，三根柱子，至少需要多少次移动才能把他们都移到第三个柱子上？很显然，在没有其他柱子时，问题的解是2^(n-1)，但现在有了这m个柱子的帮助（m<n），又该最少移动多少次呢？ ①要求输入任意的m, n都能给出正确结果。 ②要考虑任意的输入

 三、代码和注释：

# 动态规划思想，算过一次的结果存在，后面直接用
dicts = {}# 分治，穷举（优点在于有限界约束条件，多余的步骤提前结束）
def help(n,m):# 盘子数小于零没意义，柱子数小于3时已经不是汉罗塔问题，1或者2根柱子根本移不了if(n<0 or m < 3):return -1# 柱子数合理的前提下，1个盘移动一次即可if(n==1):return 1# 用元组记录当前求的是几个盘几根柱子的问题nowNM = (n,m)# 返回值为True，说明字典中保存得有当前要计算的结果if(judgeDicts(nowNM)):# 根据键取出值，即得当前要计算的结果return dicts[nowNM]# 三根柱子，可直接简化运算，返回2的盘子数次方-1（普通汉罗塔中的结论）if(m == 3):nowValue = pow(2,n)-1else:# 从起始柱子到目标柱子，柱子的排列顺序可以打乱#n-1个盘可移往m根柱子中的任意一根（顺序随意，此处为过度柱），剩下的一个盘可移往除前面那根过度柱子外的m-1根柱子中任意一根（目的柱）#n-1个盘再从过度柱移往目标柱nowValue = 2 * help(n-1,m)+help(1,m-1)# 穷举，然有限界约束条件# 过度桩盘子每递减1，目标桩盘子递增1。之前过度桩算了n-1,所以从n-2开始# 举例：4盘4柱，分为(3,4)(1,3)注意这一项在前面算过，遍历只需后两项（当然后两项也有可能被限制条件打断）；# (2,4)(2,3)；(1,4)(3,3)for i in range(n-2,0,-1):temp = 2*help(i,m)+help(n-i,m-1)# 通多数学推算，到后面的各项结果会相等，即temp=nowValue,走else分支提前跳出循环，省去多余的步骤# 原理2*前者+后者，前者权重大而后者权重小，理论上前者越小，终值越小# 但是到一定程度，前者减小的同时，后者增加的跨度极具变更大，我们要求移动次数尽量少，就不用管后面的了（数学案例总结）if(temp<nowValue):nowValue = tempelse:break# 在字典中记录当前几盘几柱的解,以便后面复用dicts[nowNM] = nowValue# print(dicts)return nowValuedef judgeDicts(nowNM):# 默认字典中没有保存当前n盘m柱的结果flag = False;# 遍历字典，如果字典的键相同，说明字典集合中，以前保存得有该结果for i in dicts:if(i==nowNM):return Truereturn flagif __name__ == '__main__':print("盘子数为：",end=" ")n = int(input())print("柱子数为：",end=" ")m = int(input())print("最少需要移动的次数为:",end=" ")print(help(n,m))

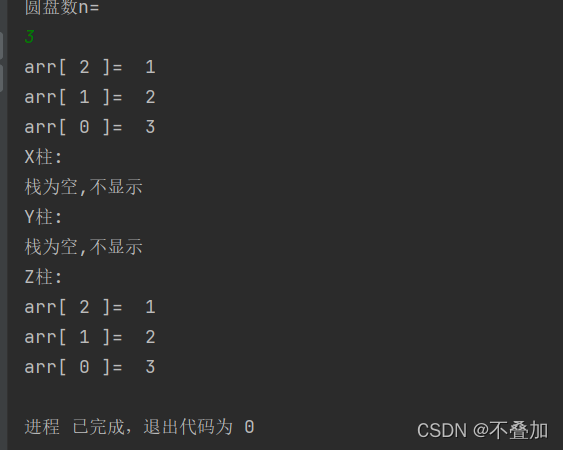
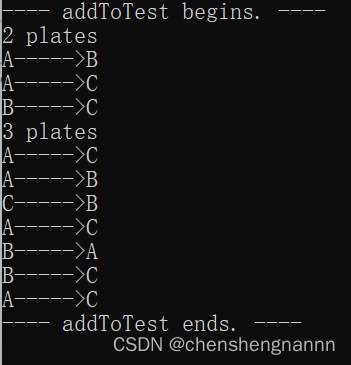
四、运行结果测试：