目录
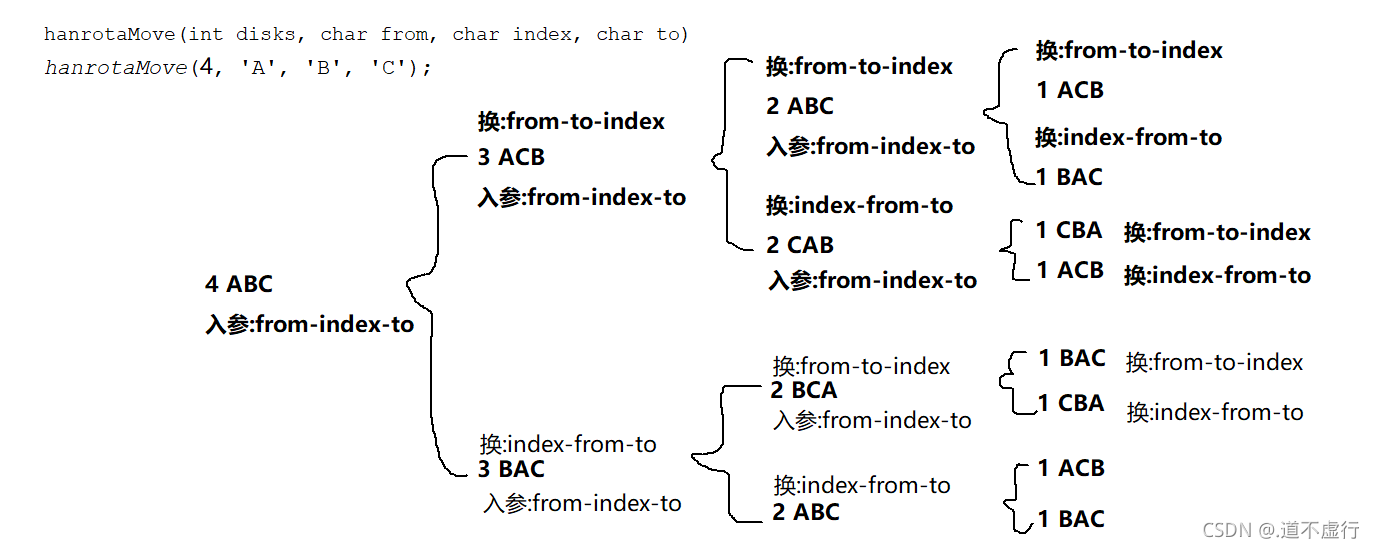
1、汉罗塔问题解决思路:
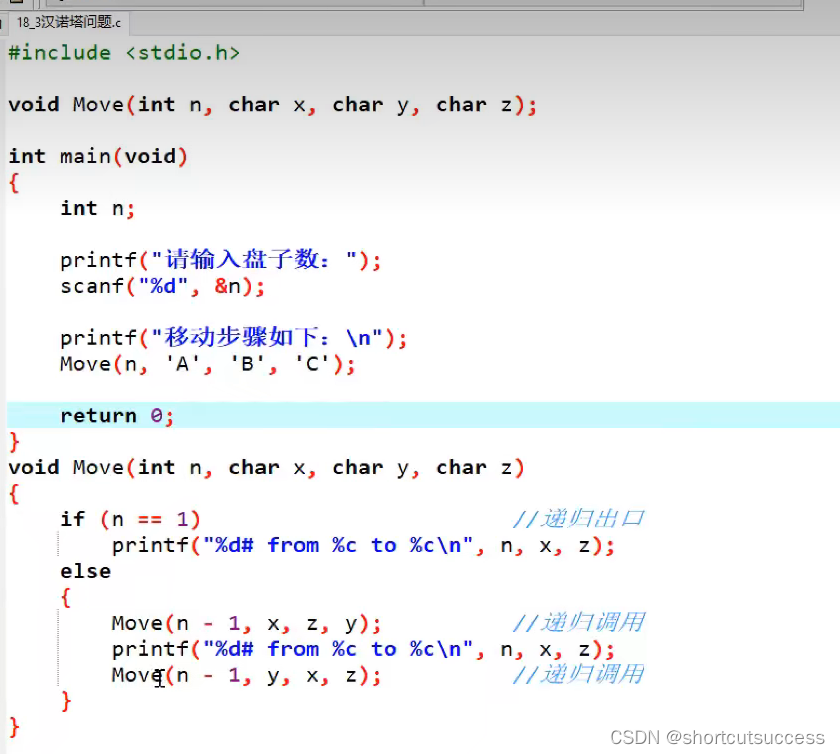
2、代码实现:
函数部分:
全部代码:
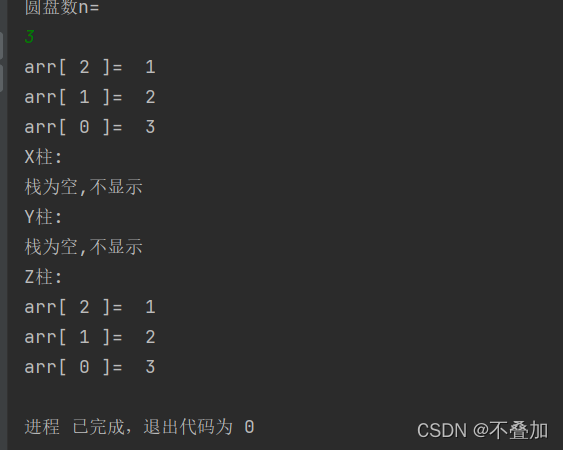
运行结果:
3、结语:
1、汉罗塔问题解决思路:
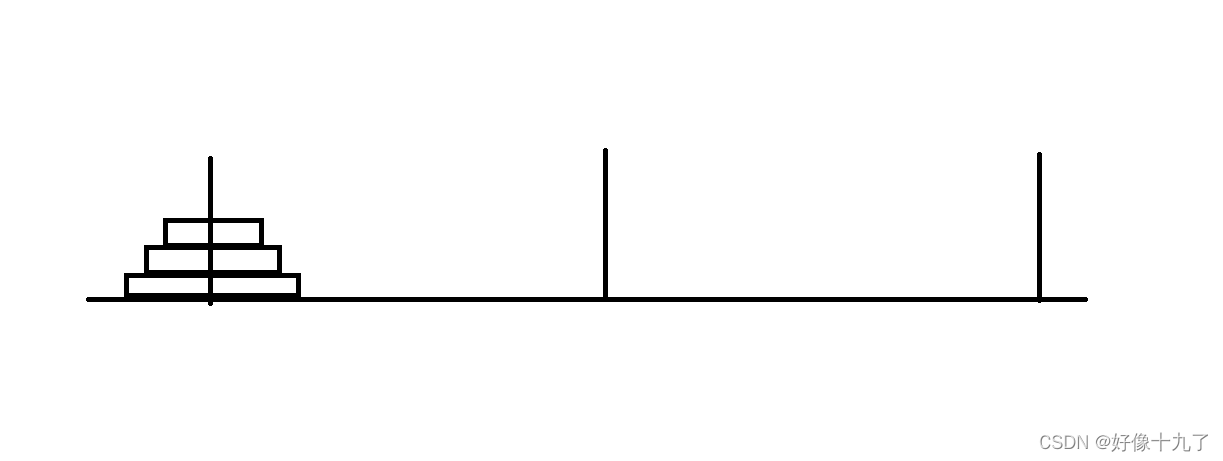
以三个为例,步骤为:
1.首先我们需要将其分成两个整体;
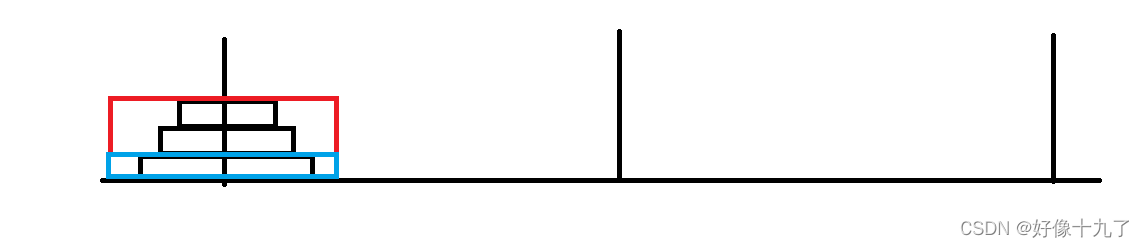
2. 然后记AC(1)=1,(1)表示最上面第一个的圆盘,AC表示从A移动至C,AC(1)表示将最第一大的一个圆盘从A移动至C;
3.具体操作:
a.我们需要计算的是AC(3)的步数;
b. AC(3)=AB(2)+AC(1)+BC(2);
c.AB(2)=AC(1)+AB(1)+CB(1);
d.BC(2)=BA(1)+BC(1)+AC(1);
f.AC(3)=AC(1)+AB(1)+CB(1)+AC(1)+BA(1)+BC(1)+AC(1)=7;
所以将最上面三个从A移动至C最少总共需要7步;
假如有n个圆盘:
AC(n)=AB(n-1)+AC(1)+BC(n-1);
2、代码实现:
函数部分:
int AB(int n)//n为最上面的圆盘数,AB表示从A移动到B;
{if (n == 1){return 1;//最上面的一个圆盘从A移动到B需要1步;}return AC(n - 1) + AB(1) + CB(n - 1);//AB(n)=AC(n - 1) + AB(1) + CB(n - 1)
}int AC(int n)//类似与上解释
{if (n == 1){return 1;//}return AB(n - 1) + AC(1) + BC(n - 1);
}
int BA(int n)//类似与上解释
{if (n == 1){return 1;}return BC(n - 1) + BA(1) + CA(n - 1);//类似与上解释
}
int BC(int n)//类似与上解释
{if (n == 1){return 1;}return BA(n - 1) + BC(1) + AC(n - 1);
}
int CB(int n)//类似与上解释
{if (n == 1){return 1;}return CA(n - 1) + CB(1) + AB(n - 1);
}
int CA(int n)//类似与上解释
{if (n == 1){return 1;}return CB(n - 1) + CA(1) + BA(n - 1);
}全部代码:
#include<stdio.h>
int AB(int n);
int AC(int n);
int BA(int n);
int BC(int n);
int CA(int n);
int CB(int n);
int main()
{int n = 4;//有四个圆盘printf("%d", AC(n));//打印结果
}
int AB(int n)
{if (n == 1){return 1;}return AC(n - 1) + AB(1) + CB(n - 1);
}int AC(int n)
{if (n == 1){return 1;}return AB(n - 1) + AC(1) + BC(n - 1);
}
int BA(int n)
{if (n == 1){return 1;}return BC(n - 1) + BA(1) + CA(n - 1);
}
int BC(int n)
{if (n == 1){return 1;}return BA(n - 1) + BC(1) + AC(n - 1);
}
int CB(int n)
{if (n == 1){return 1;}return CA(n - 1) + CB(1) + AB(n - 1);
}
int CA(int n)
{if (n == 1){return 1;}return CB(n - 1) + CA(1) + BA(n - 1);
}
运行结果:
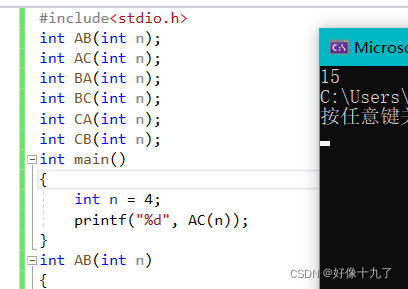
将四个圆盘A移动至C的最少步骤为15步;
3、结语:
这种算法最重要的是将繁化成简;整体思想很重要;