1 起源

汉罗塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

2 需求

将汉罗塔问题抽象到数学：

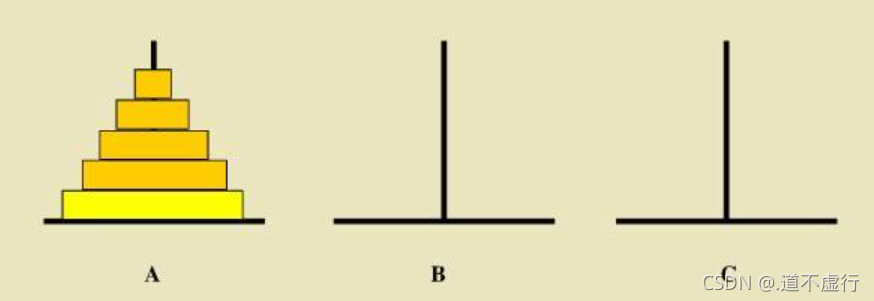
1.有三根杆子 A,B,C；
2.A 杆上有若干大小不同的碟子，从上往下越来越大；
3.每次移动一块碟子,小的只能叠在大的上面；
4.把所有碟子从 A 杆全部移到 C 杆上。

在这里插入图片描述

3 分析

确定 A 柱子上的初始碟子：int disks = 3;
确定三个容器 char ‘A’、char ‘B’、char ‘C’；
初始确定移动方法，从 from --> to：hanrotaMove(int disks, char from, char index, char to)。

3.1 1个碟子

A 柱子上只有一个碟子时，直接移动到 C：

num	from	index	to	mv
1	A	B	C	A–>C

3.2 2个碟子

num	from	index	to	mv
1	A	C	B	A–>B
2	A	B	C	A–>C
1	B	A	C	B–>C

3.3 3个碟子

num	from	index	to	mv
1	A	B	C	A–>C
2	A	C	B	A–>B
1	C	A	B	C–>B
3	A	B	C	A–>C
1	B	C	A	B–>A
2	B	A	C	B–>C
1	A	B	C	A–>C

3.4 4个碟子

num	from	index	to	mv
1	A	C	B	A–>B
2	A	B	C	A–>C
1	B	A	C	B–>C
3	A	C	B	A–>B
1	C	B	A	C–>A
2	C	A	B	C–>B
1	A	C	B	A–>B
4	A	B	C	A–>C
1	B	A	C	B–>C
2	B	C	A	B–>A
1	C	B	A	C–>A
3	B	A	C	B–>C
1	A	C	B	A–>B
2	A	B	C	A–>C
1	B	A	C	B–>C

3.5 规律

在上述前 4个下不难发现有规律存在：
A 柱子上有 n 个碟子，移动步骤便以 n 分为上下两部分，且上部分移动的数与下部分移动的数相同，此处便有递归分治的思想，解析 4 个碟子：
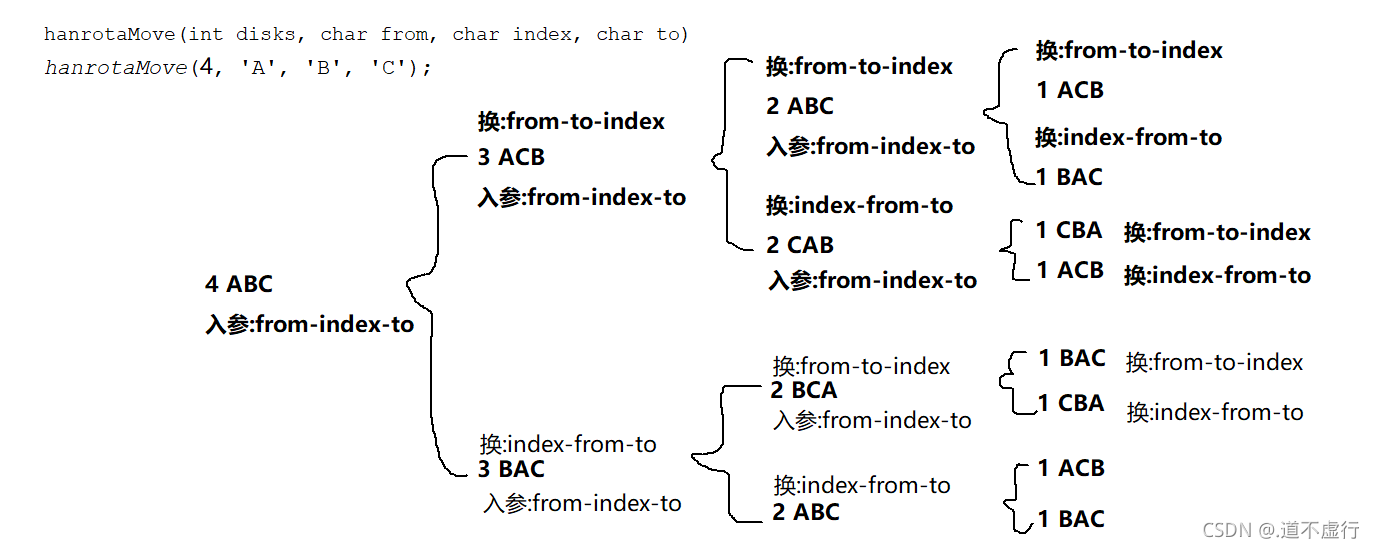
hanrotaMove(int disks, char from, char index, char to)
在初始入参：from ‘A’ - index ‘B’ - to ‘C’ 下，每一级都做为下一级分支的入参，且每个分支的上部都有相同的步骤“换”：from-to-index，每个分支的下部也都有相同的步骤“换”：index-from-to，可将此图看为完全二叉树。

4 代码实现：直接算法

代码常规实现：Hanrota.java

/*** @author zc* @date 2021/10/29 9:30* 汉罗塔*      1.有三根杆子 A,B,C；*      2.A 杆上有若干大小不同的碟子，从上往下越来越大;*      2.每次移动一块碟子,小的只能叠在大的上面；*      3.把所有碟子从 A 杆全部移到 C 杆上。*      * main(String[] args):主方法，主程序入口；* hanrotaMove(int disks, char from, char index, char to)：方法，汉罗塔移动*/
public class Hanrota {/*** 主程序入口* @param args 系统参数*/public static void main(String[] args) {// 初始化一个 A 柱子上碟子数int disks = 4;hanrotaMove(disks, 'A', 'B', 'C');}/*** 汉罗塔移动* @param disks 待移动碟子数量* @param from 起始点* @param index 过渡点* @param to 目标点*/public static void hanrotaMove(int disks, char from, char index, char to){if (disks <= 0){System.out.println("碟子数量不足");} else if (disks == 1) {System.out.println("Disk " + disks + " from " + from + " to " + to);} else {// 递归上部分hanrotaMove(disks - 1, from, to, index);// 中间分隔点System.out.println("Disk " + disks + " from " + from + " to " + to);// 递归下部分hanrotaMove(disks - 1, index, from, to);}}
}

运行结果：

Disk 1 from A to B
Disk 2 from A to C
Disk 1 from B to C
Disk 3 from A to B
Disk 1 from C to A
Disk 2 from C to B
Disk 1 from A to B
Disk 4 from A to C
Disk 1 from B to C
Disk 2 from B to A
Disk 1 from C to A
Disk 3 from B to C
Disk 1 from A to B
Disk 2 from A to C
Disk 1 from B to C

5 代码实现封装：栈的思想

汉罗塔的移动存储很像栈的思想：先进后出。

就是在上一步的代码实现：直接算法上封装一下。

首先要 java 实现一个栈，再递归分治解决汉罗塔移动：MyStack.java

package com;/*** @author zc* @date 2021/10/29 11:13* 栈：MyStack** main(String[] args)：主方法，主程序入口* MyStack(int s)：有参构造，初始化栈容器的大小* push(long j)：方法，入栈* pop()：方法，出栈* peek()：方法，获取栈顶值* isEmpty()：方法，判断栈是否为空* isFull()：方法，判断栈是否存储满* size()：方法，获取当前栈中元数存储个数* hanrotaMove(int disks, MyStack A, MyStack B, MyStack C)：方法，汉罗塔移动*/
public class MyStack {/*** 属性 maxSize：初始化栈的容器大小*/private int maxSize;/*** 属性 stackArray：栈中数据存储*/private long[] stackArray;/*** 属性 top：标志栈中最上一个元素值*/private int top;/*** 有参构造，初始化栈容器的大小* @param s 栈容器大小*/public MyStack(int s) {maxSize = s;stackArray = new long[maxSize];top = -1;}/*** 入栈* @param j 入栈的元素*/public void push(long j) {stackArray[++top] = j;}/*** 出栈* @return 返回出栈的元素*/public long pop() {return stackArray[top--];}/*** 获取栈中最上一个值* @return 返回栈顶值*/public long peek() {return stackArray[top];}/*** 判断栈是否为空* @return 返回状态为空 true,否则 false*/public boolean isEmpty() {return (top == -1);}/*** 判断栈是否存储满* @return 返回状态已满 true,否则 false*/public boolean isFull() {return (top == maxSize - 1);}/*** 求栈中当前存储元数个数* @return 返回当前存储元数个数*/public int size(){return top + 1;}/*** 主程序入口* @param args 系统参数*/public static void main(String[] args) {// 初始化栈空间int topN = 3;// 初始化 A 栈空间MyStack A = new MyStack(topN);// 初始化 B 栈空间MyStack B = new MyStack(topN);// 初始化 C 栈空间MyStack C = new MyStack(topN);// 给 A 栈添加汉罗塔数A.push(13);A.push(9);A.push(4);// 汉罗塔移动hanrotaMove(A.size(),A,B,C);// 打印 C 栈元素while (!C.isEmpty()){System.out.print(C.pop() + " ");}}/*** 汉罗塔移动* @param A A 柱子* @param B B 柱子* @param C C 柱子*/public static void hanrotaMove(int disks, MyStack A, MyStack B, MyStack C){if (disks <= 0){System.out.println("A 柱子上没有数据");} else if (disks == 1) {// A 中出栈long value = A.pop();System.out.println("Disk " + value + " from " + A + " to " + C);// C 中入栈C.push(value);} else {// 递归上部hanrotaMove(disks - 1, A, C, B);// A 中出栈long value = A.pop();System.out.println("Disk " + value + " from " + A + " to " + C);// C 中入栈C.push(value);// 递归下部hanrotaMove(disks - 1, B, A, C);}}
}

运行结果：

Disk 4 from com.MyStack@74a14482 to com.MyStack@1540e19d
Disk 9 from com.MyStack@74a14482 to com.MyStack@677327b6
Disk 4 from com.MyStack@1540e19d to com.MyStack@677327b6
Disk 13 from com.MyStack@74a14482 to com.MyStack@1540e19d
Disk 4 from com.MyStack@677327b6 to com.MyStack@74a14482
Disk 9 from com.MyStack@677327b6 to com.MyStack@1540e19d
Disk 4 from com.MyStack@74a14482 to com.MyStack@1540e19d
4 9 13