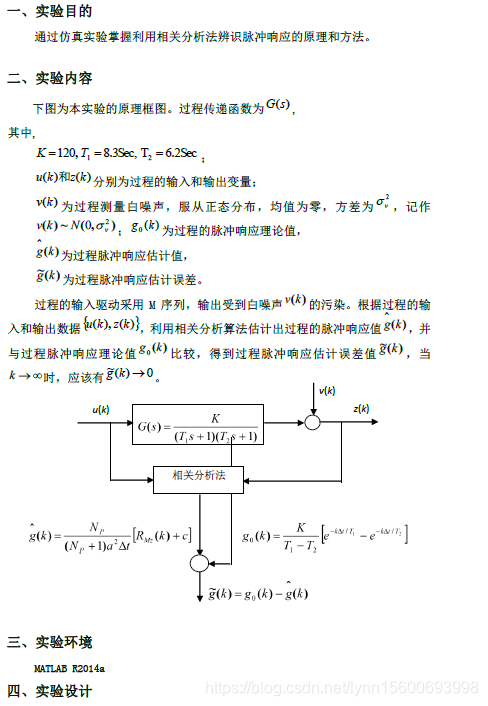
主程序:
%% 参数初始化 times=1; Np=63;%2^6-1,输入序列循环周期 N=252*times; a=1;%输入序列幅值 T0=1;%采样时间 delta_g=zeros(200,1); ratio_vy=zeros(200,1); %% 人机对话 sigma=input('请输入噪声标准差: '); r=input('请输入循环周期数(本程序中,输入2或3): '); % sigma=0.1; % for r=1:200 %% 生成输入序列 u=createM(Np,a,N); %% 生成噪声序列 v=createV(sigma,N); %% 生成理论值 y=transform(u,T0,N); z=y+v; %% 计算脉冲响应理论值 g0=calculateg0(T0,Np); %% 计算脉冲响应估计值 g1=calculate_z(Np,r,a,u,z,T0); %% 脉冲响应估计误差 g=g0-g1; temp=sqrt(sum(g.^2)/sum(g0.^2)); delta_g(r)=temp; %% 噪信比计算(方差是标准差的平方) d_v=var(v);%噪声方差 d_y=var(y);%过程输出方差 ratio_vy(r)=sqrt(d_v/d_y);%噪信比 % end % 画图 %脉冲响应理论值与估计值的比较 % subplot(1,2,1) figure(1) t=linspace(0,62,63); plot(t,g0,'-b','LineWidth',2); hold on plot(t,g1,'--r','LineWidth',2); title('脉冲响应理论值与估计值') legend('脉冲响应理论值','脉冲响应估计值');%加入噪声前后的输出序列比较 % subplot(1,2,2) figure(2) t=linspace(0,(N-1),N); plot(t,y,'-b','LineWidth',1.5); hold on plot(t,z,'--r','LineWidth',1.5); title('加入噪声前后的输出序列比较') legend('不含噪声的输出序列','含噪声的输出序列'); ylim([-40 40]);
2、输入序列
%% 输入数据 M序列
function u=createM(Np,a,N)
%赋初值
M=[0 0 0 0 0 0 1];
for k=1:NM(1)=M(7)+M(6);if M(1)==2M(1)=0;endfor i=7:-1:2M(i)=M(i-1);endif M(1)==0u(k)=a;endif M(1)==1u(k)=-a;endend
end3、噪声序列
%扰动信号 白噪声序列
function v=createV(sigma,N)
%赋初值
M=32768;
A=179;
x=zeros(1,12*N);
x(1)=11;
%% 生成均匀分布数列
temp=x(1)/M;
x(1)=A*temp-floor(A*temp);for i=2:12*Nx(i)=A*x(i-1)-floor(A*x(i-1));end
%% 生成正态分布数列for k=1:Nksai=0;for i=(12*k-11):12*k ksai=ksai+x(i);endv(k)=sigma*(ksai-6);end
end4、生产理论值
% 传递函数
function Y=transform(u,T0,N)
K=120;
T1=8.3;
T2=6.2;
K1=K/(T1*T2);
E1=exp(-T0/T1);
E2=exp(-T0/T2);
x(1)=0;
y(1)=0;for k=2:Nx(k)=E1*x(k-1)+T1*K1*(1-E1)*u(k-1)+T1*K1*(T1*(E1-1)+T0)*(u(k)-u(k-1))/T0;y(k)=E2*y(k-1)+T2*(1-E2)*x(k-1)+T2*(T2*(E2-1)+T0)*(x(k)-x(k-1))/T0;end
Y=y;
end 5、脉冲响应理论值
function g0=calculateg0(T0,Np)
K=120;
T1=8.3;
T2=6.2;
E1=-T0/T1;
E2=-T0/T2;
K1=K/(T1-T2);
for k=1:Nptemp(k)=K1*(exp(k*E1)-exp(k*E2));
end
g0=temp;
end6、脉冲响应估计值
%计算估计值
function g1=calculate_z(Np,r,a,u,z,T0)for k=1:Nptemp=0;for i=(Np+1):(r+1)*Nptemp=temp+u(i-k)*z(i);endRmz(k)=temp/(r*Np);end
c=-Rmz(Np-1);for k=1:Nptemp1(k)=Np*(Rmz(k)+c)/((Np+1)*a*a*T0);endg1=temp1;
end7、画图程序
% 画图
%脉冲响应理论值与估计值的比较
% subplot(1,2,1)
figure(1)
t=linspace(0,62,63);
plot(t,g0,'-b','LineWidth',2);
hold on
plot(t,g1,'--r','LineWidth',2);
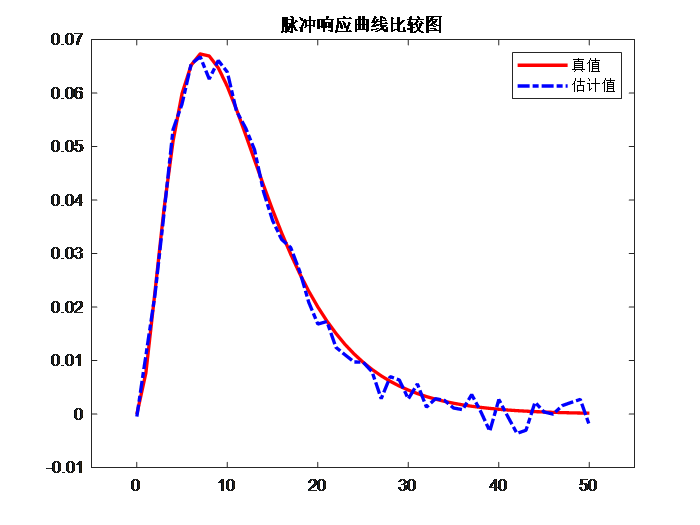
title('脉冲响应理论值与估计值')
legend('脉冲响应理论值','脉冲响应估计值');%加入噪声前后的输出序列比较
% subplot(1,2,2)
figure(2)
t=linspace(0,(N-1),N);
plot(t,y,'-b','LineWidth',1.5);
hold on
plot(t,z,'--r','LineWidth',1.5);
title('加入噪声前后的输出序列比较')
legend('不含噪声的输出序列','含噪声的输出序列');
ylim([-40 40]); 
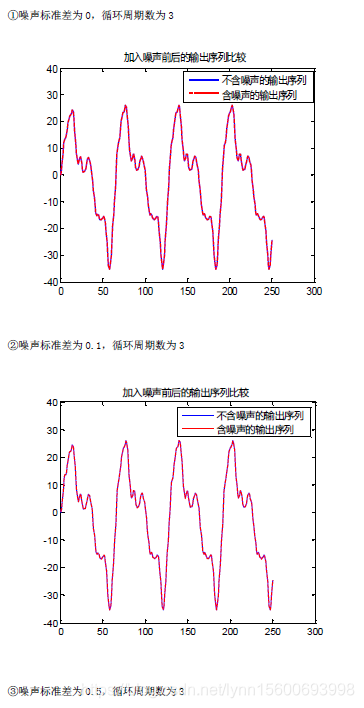

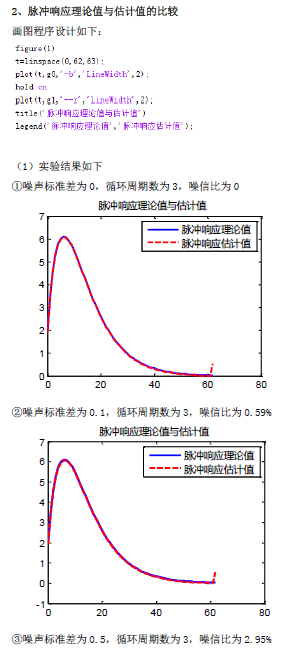
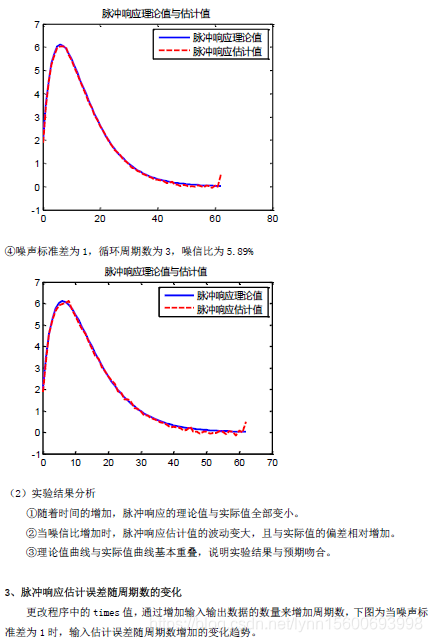
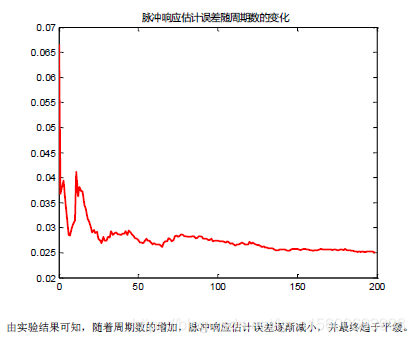
该实验中,脉冲响应估计误差最后保持在0.025左右。后续实验可以尝试通过利用逆M序列来替代M序列或进一步增加周期数等方式来进一步提高实验准确度。
参考资料
1、实验一指导书,孙应飞
2、过程辨识,方崇智 萧德云,清华大学出版社
3、https://wenku.baidu.com/view/1df4d12f284ac850ad0242c7.html