前言

在过程控制系统的学习中，测量一个被控对象的阶跃响应非常重要，因为根据阶跃响应曲线可以得到被控对象的许多非常重要的参数。而有一个非常重要的测量阶跃响应曲线的方法是矩形脉冲响应曲线法。在学习的过程中，我走了一些弯路，便在这里把自己的学习经验分享给大家。

本文主要包含以下几个内容：

• 矩形脉冲响应曲线的定义；
• 矩形脉冲响应曲线和阶跃响应曲线之间的关系及绘制阶跃响应曲线；
• 使用 Python 完成阶跃响应曲线的绘制。

本文主要参考书籍为：李国勇.《过程控制系统》（第3版）. 北京. 电子工业出版社. 2017

下面，我们正式开始👇

---

一、矩形脉冲响应曲线的定义

矩形脉冲响应曲线的定义：用矩形脉冲输入代替通常的阶跃输入，即大幅度的阶跃扰动施加一小段时间之后立即将它切除。这样得到的矩形脉冲响应不同于正规的阶跃响应，但两者之间关系密切，可以用矩形脉冲响应曲线求取对应的阶跃响应曲线。

用矩形脉冲响应曲线的原因：为防止被控量变化超过允许范围，生产实际不允许有较长时间和较大幅度的输入变化。这时可用矩形脉冲信号作为过程的输入信号，测出过程的矩形脉冲响应曲线（阶跃响应曲线由于测试时间较长而不合适），转化为阶跃响应曲线对参数估计。

---

二、绘制阶跃响应曲线

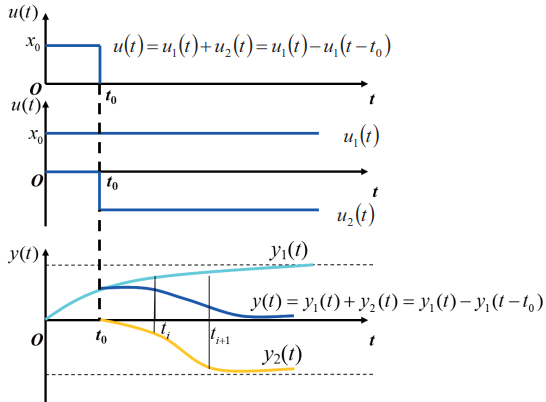
变换方法：输出响应可看作由两个时间相差 $t_0$、极性相反、形状完全相同的阶跃响应的叠加而成。所以：$y_2(t)=y_1(t-t_0)$，$y(t)=y_1(t)+y_2(t)=y_1(t)-y_1(t-t_0)$，$y_1(t)=y(t)+y_1(t-t_0)$，其中 $y_1(t)$ 为阶跃响应值，$y(t)$ 为矩形脉冲响应值。

注意：

• 并不是一直叠加即可，一直叠加只是采样时间和脉冲时长相等时的特殊情况。
• 由于变换方法的限制，采样的时间点一定是等间隔的。

例题：已知某一液位对象，其矩形脉冲相应的实验数据如下：

t/s	0	10	20	40	60	80	100	120	140	160	180
h/cm	0	0	0.2	0.6	1.2	1.6	1.8	2.0	1.9	1.7	1.6
t/s	200	220	240	260	280	300	320	340	360	380	400
h/cm	1.0	0.8	0.7	0.65	0.6	0.5	0.4	0.3	0.2	0.15	0.1

已知矩形脉冲赋值 $\Delta u(t)=20\%$ 阀门开度变化，脉冲宽度 $\Delta t=20s$，试将矩形脉冲响应转化为阶跃响应。

解答：找到 $20s$ 点，其实际值为 $2.0+0$，$20s$ 之前的均为阶跃响应的值，之后的就是矩形脉冲响应值。所以 $y_1(40)=y(40)+y_1(40-20)$，即 $y_1(40)=0.6+0.2=0.8$。之后依次计算，即可得到最终的阶跃响应曲线的值。

---

三、编程绘制阶跃响应曲线

1、流程图

2、Python

使用较为常用的 Python 进行编程实现，使用 Numpy、Matplotlib 两个常用库。

源码如下：

import numpy as np
import matplotlib.pyplot as plt# 初始化
t0 = 20
t1 = 20
n = int(t0 / t1)
y = np.array([0, 0.2, 0.6, 1.2, 1.6, 1.8, 2.0, 1.9, 1.7, 1.6, 1,0.8, 0.7, 0.7, 0.6, 0.6, 0.4, 0.2, 0.2, 0.15, 0.15])
x = np.linspace(start=0, stop=400, num=y.size)
y1 = np.zeros([y.size])# 找阶跃响应消失点
# 消失点之前直接赋值
y1[0:n] = y[0:n]
# print(y1)# 消失点之后加间隔数
index = 0
while index <= (y.size - n - 1):y1[n + index] = y1[index] + y[n + index]index += 1# 绘图
plot = plt.plot(x, y1)
plt.show()

3、结果

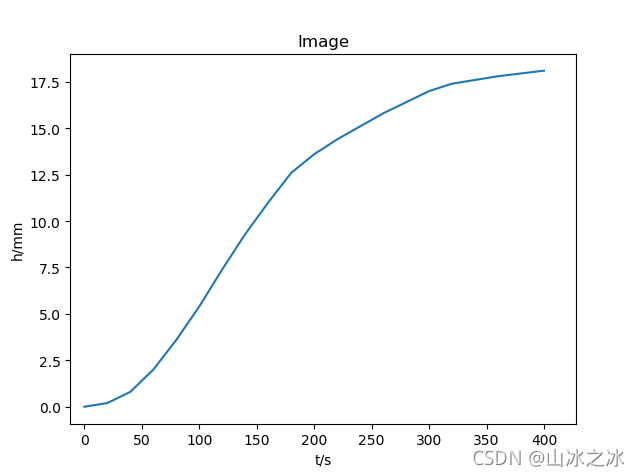
总结

本文先介绍了矩形脉冲响应曲线的定义，后分析了使用矩形脉冲响应曲线的原因。之后讲解了如何将矩形脉冲响应曲线转换为阶跃响应曲线，并提供了 Python 的程序绘制阶跃响应曲线。