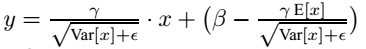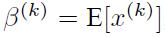归一化

1.归一化含义

归纳统一样本的统计分布性。归一化在0~1之间是统计的概率分布，归一化-1~1之间是统计的坐标分布。
无论是为了建模还是为了计算，首先基本度量单位要统一，神经网络是以样本在事件中的统计分别几率来进行训练（概率计算）和预测，且sigmoid函数的取值是0-1之间的，网络最后一个节点的输出也是如此，所以经常要对样本的输出归一化处理。
归一化是统一在0-1之间的统计概率分布，当所有样本的输入信号都为正值时，与第一隐含层神经元相连的权值只能同时增加或减少，从而导致学习速度很慢。
另外在数据中常存在奇异样本数据，奇异样本数据存在所引起的网络训练时间增加，并可能引起网络无法收敛。为了避免出现这种情况及后面数据处理的方便，加快网络学习速度，可以对输入信号进行归一化，使得所有样本的输入信号其均值接近于0或与其均方差相比很小。

2.为什么要归一化?

为了后面数据处理的方便，归一化的确可以避免- -些不必要的数值问题。
为了程序运行时收敛加快。
同一量纲。样本数据的评价标准不一样，需要对其量纲化,统一评价标准。这算是应用层面的需求。
避免神经元饱和。啥意思?就是当神经元的激活在接近0或者1时会饱和，在这些区域，梯度几乎为0,这样，在反向传播过程中，局部梯度就会接近0,这会有效地”杀死"梯度。
保证输出数据中数值小的不被吞食。

3.为什么归一化能提高求解最优解速度？

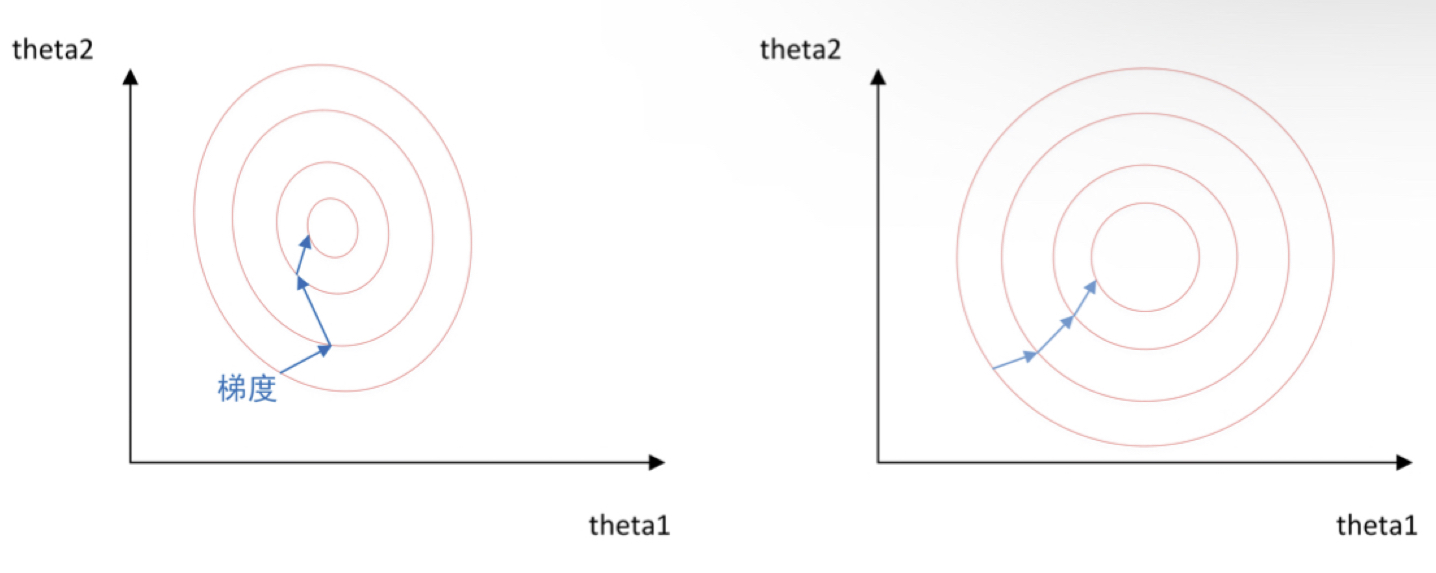
        上图是代表数据是否均一化的最优解寻解过程(圆圈可以理解为等高线)。左图表示未经归一化操作的寻解过程，右图表示经过归一化后的寻解过程。
        当使用梯度下降法寻求最优解时，很有可能走"之字型"路线(垂直等高线走)，从而导致需要迭代很多次才能收敛;而右图对两个原始特征进行了归一化，其对应的等高线显得很圆，在梯度下降进行求解时能较快的收敛。
        因此如果机器学习模型使用梯度下降法求最优解时，归一化往往非常有必要，否则很难收敛甚至不能收敛。

为什么引入BN？

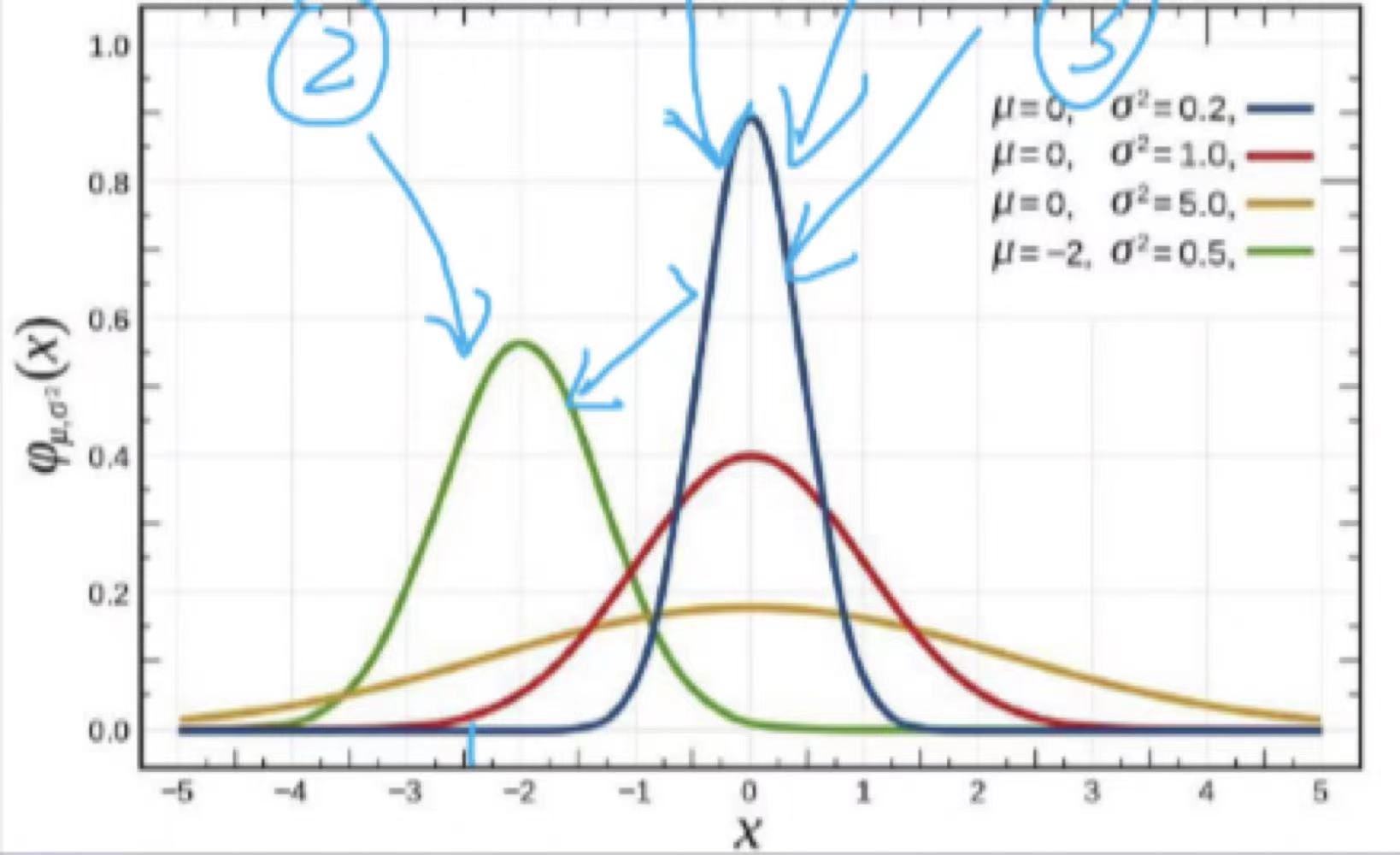
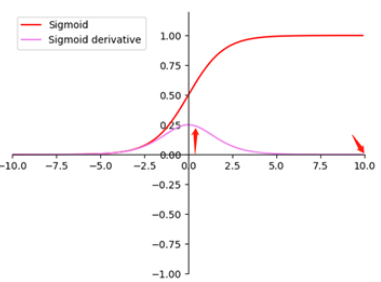
为加速网络的训练，在图像预处理时，我们就后对图像进行标准化操作，即image normalization，是的每张图片都能服从u均值σ标准差的分布。但是当图片输如到神经网络后，每经过一次卷积，数据就不会再服从该分布，这种现象叫做ICS（Internal Covariate Shift，内部协变量偏移），该现象会使输入分布变化，导致模型的训练困难，对深度神经网络影响极大，如左图所示，数据分布不统一，深层网络就需要去适应这些数据分布，从而导致网络训练速度慢。如果不进行归一化，直接进行激活，很可能一些新的数据会落入激活函数的饱和区，导致神经网络训练的梯度消失，如右图所示当feature map的数据为10的时候，就会落入饱和区，影响网络的训练效果。这个时候我们引入Batch Normalization的目的就是使我们卷积以后的feature map满足均值为0，方差为1的分布规律。BN本质是解决梯度消失的问题。

BN的作用原理

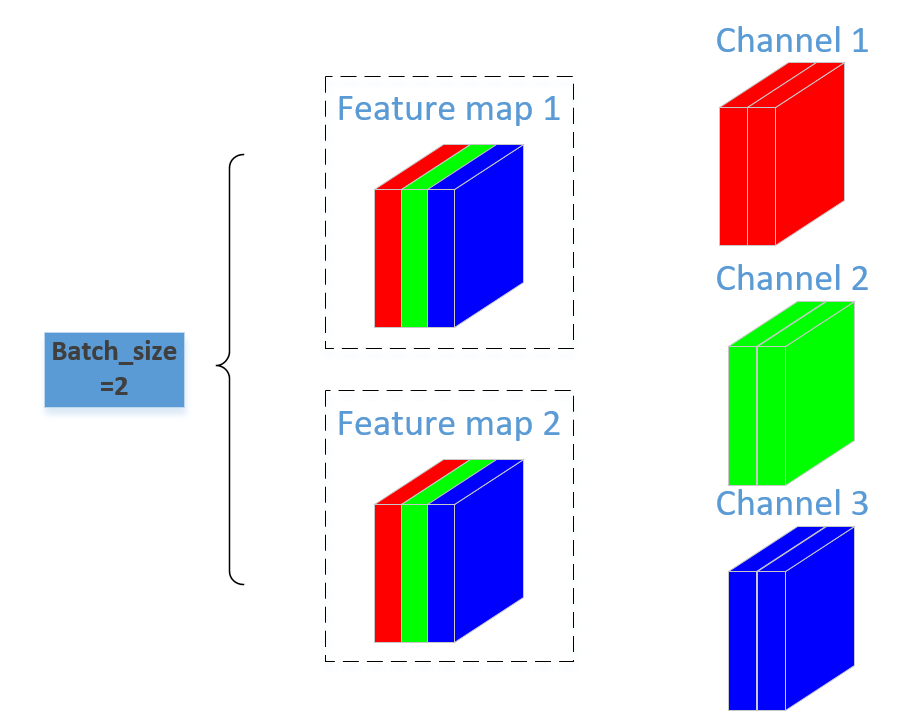
BN作用位置：BN是对同一个batch中不同样本图片（输入的image）之间的同一channel的神经元（像素）进行归一化。

如图所示，一个batch中有两个图片，每个图片有三个通道，我们进行BN的位置就是对该batch中不同图片的相同通道的像素进行归一化计算。

BN前向推导公式：

下面我们用一个例子来看看BN是如何计算的，以batchsize=2为例，每个feature map有两个通道。

首先对两个feature的相同位置的通道如channel1，计算整个channel1的均值 $u_{1}$ =1和方差 $\sigma _{1}^{2}$ =1，然后将channel1中每个像素减均值除标准差，得到右边归一化数据。同理，channel2做相同操作，得到归一化后的数据。最后将归一化后的每一个像素乘γ（缩放因子）加β（平移因子）得到BN的结果。

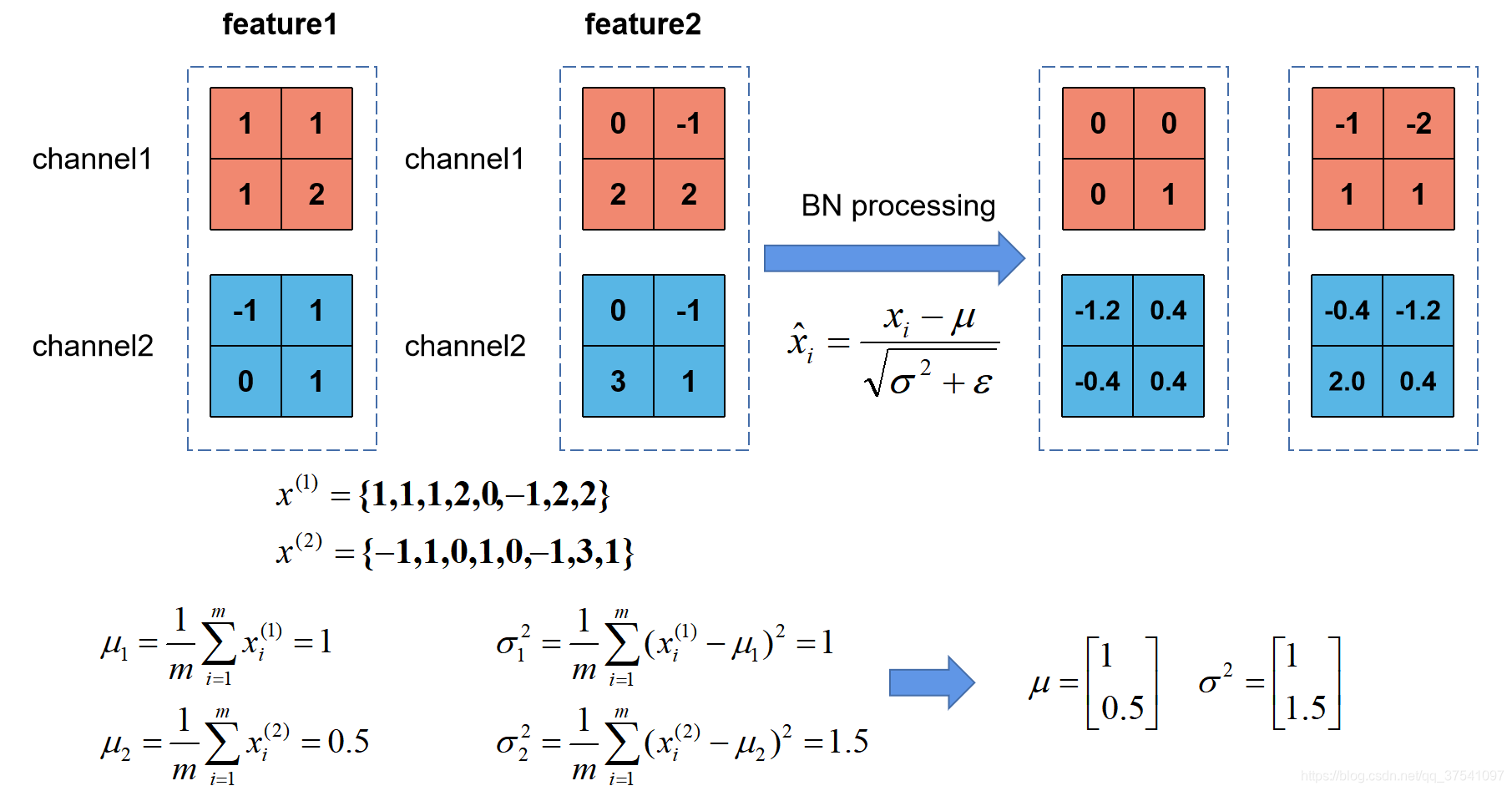
为什么引入γ和β？

BN首先是得输入Normalization，对数据的分布进行额外的约束，使其变成均值为0，方差为1的分布，增强模型的泛化能力。normalization缓解了ICS，使得每一层的输入变得稳定，但是同时也降低了模型的拟合能力，缺乏了数据原有的表达能力，使得底层学习到的信息丢失，并且均值为0，方差为1，在经过sigmoid的时候，容易陷入到其线性区域，破坏了之前学习到的特征分布。所以引入γ（缩放因子）和β（平移因子），恢复数据的表达能力，对规范后的数据进行线性变换，与之前的网络层解耦，从而更加有利于优化的过程，提高模型的泛化能力。

BN的优点

减少梯度消失，加速网络训练，提高训练精度。
防止过拟合。
减少了对学习率的要求。可以使用初始很大的学习率或者选择了较小的学习率，算法也能够快速训练收敛。
减少人为选择参数。减少对初始化的依赖，在某些情况下可以取消dropout和L2正则项参数，或者采取更小的L2正则约束参数。

为什么BN可以加速网络训练？

低层的微弱变化会引起高层的输入分布的变化，高层的网络需要不断地调整去适应输入的变化。从而导致收敛速度慢，学习速度慢。所以在没有使用BN之前，我们都要选择一个小的学习率和合适的初始化参数。

BN的不足

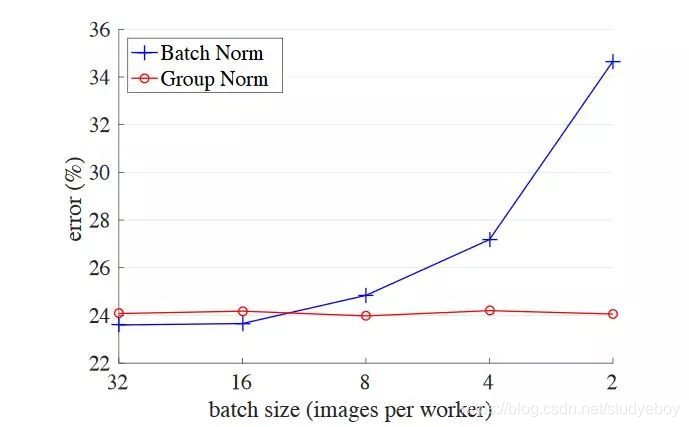
当batch size较小时（如2、4），该batch数据的均值和方差的代表性较差，因此对最后的结果影响也较大。随着batch size越来越小，BN层所计算的统计信息的可靠性越来越差，这样就容易导致最后错误率的上升；而在batch size较大时则没有明显的差别。虽然在分类算法中一般的GPU显存都能cover住较大的batch设置，但是在目标检测、分割以及视频相关的算法中，由于输入图像较大、维度多样以及算法本身原因等，batch size一般都设置比较小，所以GN对于这种类型算法的改进应该比较明显。

如上图，可见 BN 随着 batchsize 减小，性能下降比较明显。
由于BN训练的时候是基于一个 mini-batch 来计算均值和方差的，这相当于在梯度计算时引入噪声，如果 batchsize 很小的话， BN 就有很多不足。不适用于在线学习（batchsize = 1）当数据是大图片，并且一个batch一般都只有1-2张图片，不建议使用 BN。

为什么BN层一般在线性层和卷积层后面，而不是放在非线性单元后面?
因为非线性单元的输出分布形状会在训练过程中发生变化，归一化无法消除他的方差偏移，相反的，全连接层和卷积层的输出是一个对称的，非稀疏的分布，类似于高斯分布，对他们进行归一化会产生更加稳定的分布。如果像relu这样的激活函数，如果输入的数据是一个高斯分布，经过它变换之后的数据是什么形状？小于0的被抑制了，也就是分布小于0的部分直接变成0了。

BN比较适用的场景：

每个mini-batch比较大，数据分布比较接近。在进行训练之前，要做好充分的shuffle，否则效果会差很多。另外，由于BN需要在运行过程中统计每个mini-batch的一阶统计量和二阶统计量，因此不适用于动态的网络结构和RNN网络。

注意：

训练和测试时BN是不同的：训练时的均值方差来源于当前的mini-batch数据，而测试时，则要使用训练使用过的全部数据的均值方差，这一点训练时就通过移动均值方法计算并保存下来了。

使用BN时需要注意的问题
（1）训练时要将traning参数设置为True，在验证时将trainning参数设置为False。在pytorch中可通过创建模型的model.train()和model.eval()方法控制。
（2）batch size尽可能设置大点，设置小后表现可能很糟糕，设置的越大求的均值和方差越接近整个训练集的均值和方差。
（3）一般将bn层放在卷积层（Conv）和激活层（例如Relu）之间，且卷积层不要使用偏置bias，该偏置可被BN层中的β给抵消掉。
下面我来用公式证明为什么不要使用篇置：

BN、LN、IN和GN之间的区别

BatchNorm：batch 方向做归一化，算 N ∗ H ∗ W 的均值
LayerNorm：channel 方向做归一化，算 C ∗ H ∗ W的均值
InstanceNorm：一个 channel 内做归一化，算 H ∗ W 的均值
GroupNorm：将 channel 方向分 group ，然后每个 group 内做归一化，算( C / / G ) ∗ H ∗ W 的均值

针对每一个 γ 和 β，GN 是对每一个 channel 进行学习的

其中两维 C 和 N 分别表示 channel 和 batch size，第三维表示 H,W，可以理解为该维度大小是 H ∗ W ，也就是拉长成一维，这样总体就可以用三维图形来表示。可以看出 BN 的计算和 batch size 相关（蓝色区域为计算均值和方差的单元），而 LN、BN 和 GN 的计算和 batch size 无关。同时 LN 和 IN 都可以看作是 GN 的特殊情况（LN 是 group=1 时候的 GN，IN 是 group=C 时候的GN）。