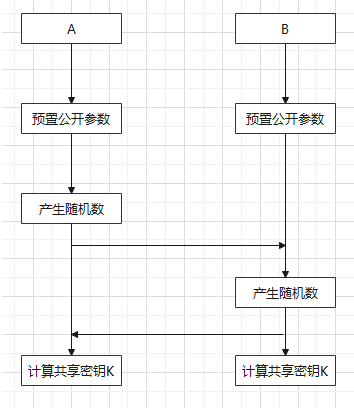
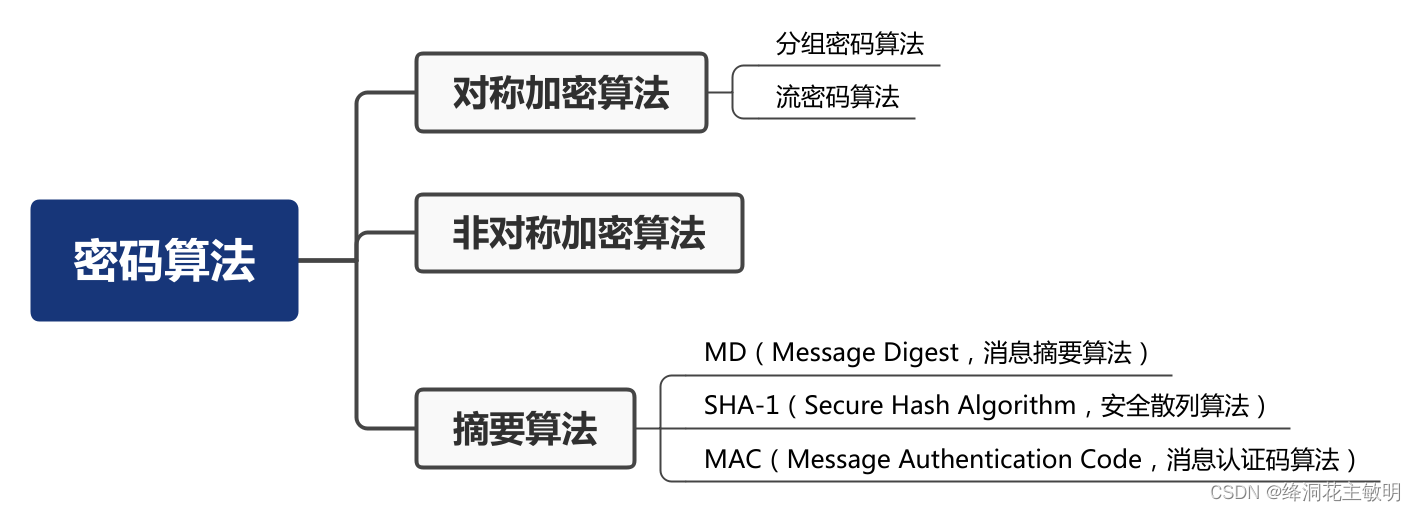
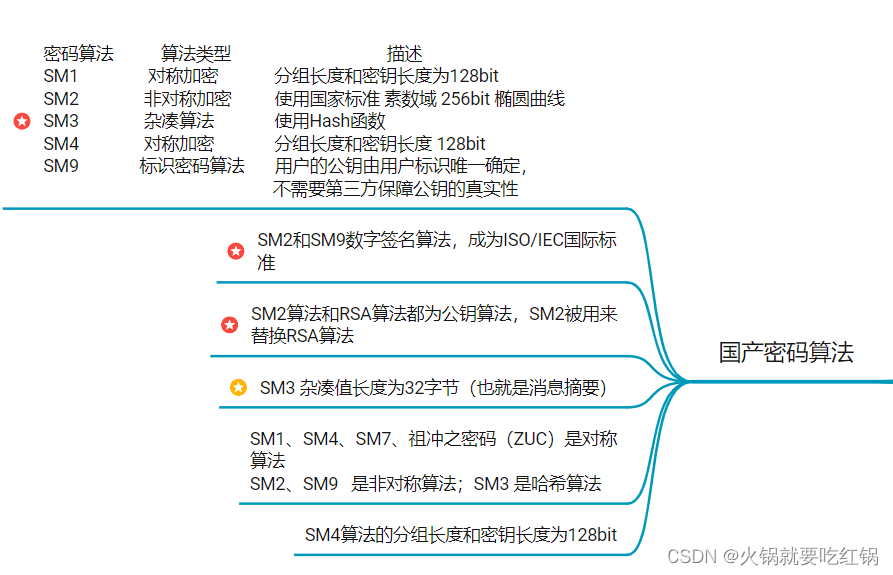
参考推荐：

国家密码管理局关于发布《SM2椭圆曲线公钥密码算法》公告（国密局公告第21号）_国家密码管理局

https://blog.csdn.net/u013137970/article/details/84573200

图片来源于：图解SM2算法流程（合）_网糸隹的博客-CSDN博客_sm2算法原理

SM2椭圆曲线公钥密码算法

SM2算法是国家密码据于2010年12月17日发布的国密标准椭圆曲线加密算法。对于一般椭圆曲线的离散对数问题，目前只存在指数级计算复杂度的求解方法。与大数分解问题及有限域上离散对数问题相比，椭圆曲线离散对数问题的求解难度要大得多。因此，在相同安全程度要求下，椭圆曲线密码较其他公钥密码所需的秘钥规模要小得多。

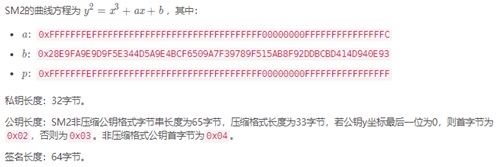
1、基础参数以及密钥对生成

基础参数：

密钥对生成：

2、加解密

       设需要发送的消息为比特串M，klen为M的长度，对M加密流程：

1. 用随机数发生器产生随机数k∈[1,n-1];
2. 计算椭圆曲线点C1=[k]G=(x1,y1)，并将C1的数据类型转换为比特串；
3. 计算椭圆曲线点S=[h]PB，若S为无穷远点，则报错并退出；
4. 计算椭圆曲线点[k] PB =(x2,y2)，将坐标x2、y2的数据类型转换为比特串；
5. 计算t=KDF(x2∥y2,klen)，若t为全0比特串，则返回1）；
6. 计算C2=M⊕t；
7. 计算C3=Hash(x2∥M∥y2);
8. 输出密文C=C1∥C2∥C3。

       设klen为C2的比特长度，对密文C=C1∥C2∥C3解密流程：

1. 从C中取出比特串C1，将C1的数据类型转换为椭圆曲线上的点，验证C1是否满足椭圆曲线方程，若不满足则报错并退出；
2. 计算椭圆曲线点S=[h]C1，若S为无穷远点，则报错并退出；
3. 计算[dB]C1=(x2,y2)，将坐标x2、y2的数据类型转换为比特串；
4. 计算t=KDF(x2∥y2,klen)，若t为全0比特串，则报错并退出；
5. 从C中取出比特串C2，计算M’=C2⊕t;
6. 计算u=Hash(x2∥M’∥y2)，从C中取出比特串C3，若u≠C3，则报错并退出；
7. 输出明文M’。

3、签名、验签

预处理1：

预处理2：

签名：

验签：

签名验证原理：

补：SM2、SM3协同工作：

注：

如有错误、侵权，请联系笔者更改删除！！！