EIGamal公钥密码算法

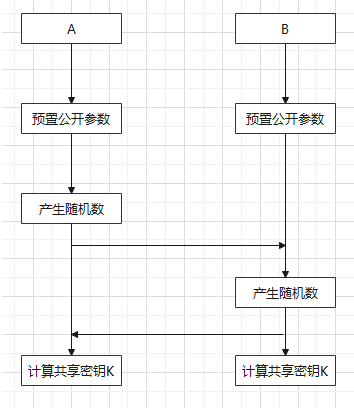
ElGamal公钥密码算法是1985年由塔希尔·盖莫尔提出，是一个基于迪菲-赫尔曼密钥交换的非对称加密算法，是在密码协议中有着重要应用的一类公钥密码算法，其安全性是基于有限域上离散对数学问题的难解性。它至今仍是一个安全性良好的公钥密码算法，是一种既可用于加密又可用于数字签名的公钥密码算法。

一、相关数学基础

有限域、阶、本原元

二、算法原理

ElGamal算法的可靠性基础：有限域上离散对数的问题的难解性。

三、算法详细流程

1、参数定义和密钥生成

取大素数 p ，要求p-1有大素数因子，再选择一个模p的本原元g;
随机选取一整数 x （2 <= x <= (p - 2)，
计算 y = g^x (mod p)
(p，g，x) 是私钥、（(p，g，y) 是公钥

2、加、解密、签名

加密M：

假定：用户A发送明文M给用户B，A加密明文M得到密文C；
A将M编码为一个在0到p-1之间的整数m作为传输的明文；
随机选取一整数 r （2 <= r<= (p - 2) 且 k 与 (p - 1) 互素）；
计算 c1= g^r mod p，c2 = m*y^r mod p（y为用户B的公钥）；
得到密文 C = (c1, c2)；
用户A把密文C传给用户B；

解密C:

用户B接受到密文，计算明文m;
m = c2 * c1^(-x) mod p ;（ｘ为用户B的私钥）
注解：c2 * c1^(-x) mod p Ξ m * y^r * g^(-xr) Ξ m * g^(xr) * g^(-xr) Ξ m

签名：

四、特点和安全性

引入随机数：增强了算法的不确定性；
参数选取：参数P应足够大，应为150位以上的十进制数，且P-1应有大素数因子；r及解密密钥不应太小；加密使用的随机数必须是一次性的；
应用：GnuPG和PGP等很多密码学系统。

ElGamal加密过程需要两次模指数运算和一次模乘积运算，解密过程需要模指数运算，求逆运算和模乘积运算各一次。每次加密运算需要选择一个随机数，所以密文既依赖于明文，又依赖于选择的随机数，故对于同一个明文，不同的时刻生成的密文不同。另外，El-Gamal加密使得消息扩展了两倍，即密文的长度是对应明文长度的两倍。

注：

如有错误、侵权，请联系笔者更改删除！！！