密码学学习笔记（二）——对称密码算法（轻量级密码算法Twine）

article/2025/9/25 2:25:56

文章目录

  • 1. 分组密码（Twine）
    • 1.1 加解密方式
      • 1.1.1 加密
      • 1.1.2 密钥生成算法
      • 1.1.3 解密
      • 1.1.4 全部代码
    • 1.2. 分组密码的模式
      • 1.2.1 ECB模式
      • 1.2.2 CBC模式
      • 1.2.3 CFB模式
      • 1.2.4 OFB模式
      • 1.2.5 CTR模式
  • 2.序列密码

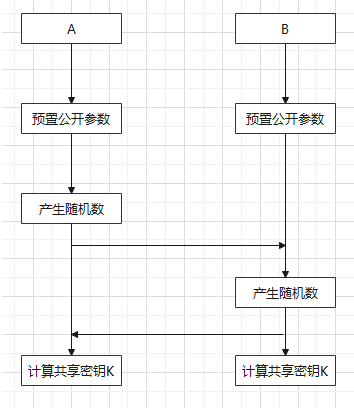
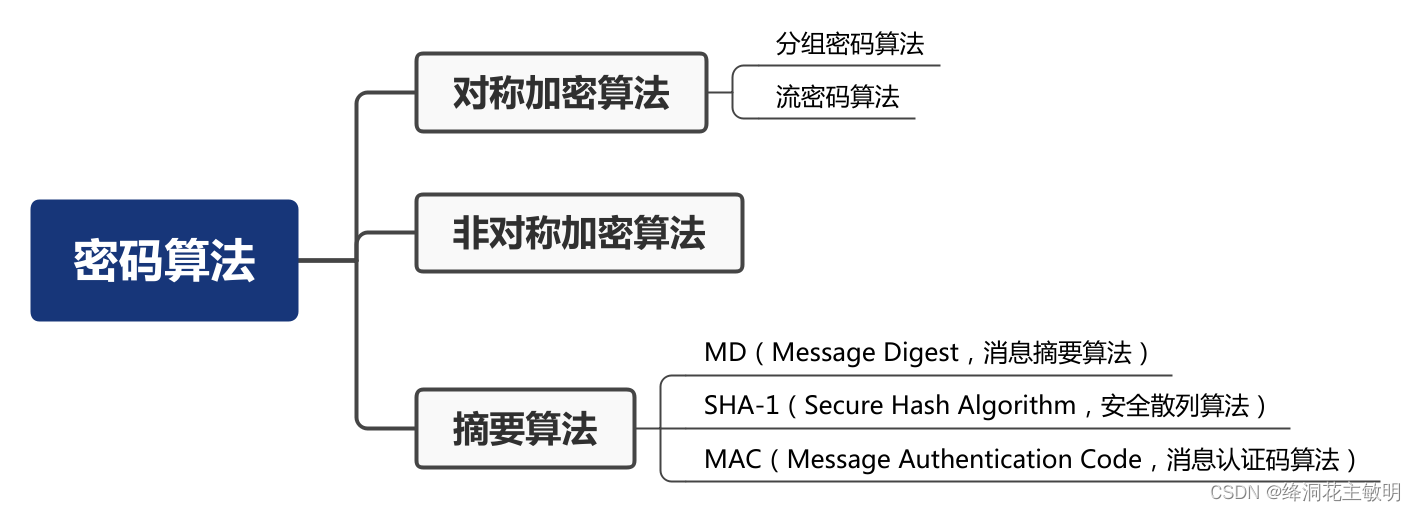
如图，对称加密算法是应用较早的加密算法，技术成熟。在对称加密算法中，数据发信方将明文和加密密钥一起经过特殊加密算法处理后，使其变成复杂的加密密文发送出去。收信方收到密文后，若想解读原文，则需要使用加密用过的密钥及相同算法的逆算法对密文进行解密，才能使其恢复成可读明文。具有算法公开、计算量小、加密速度快、加密效率高等特点。在这里插入图片描述

1. 分组密码（Twine）

Twine是由Tomoyasu Suzaki，Kazuhiko Minematsu， Sumio Morioka和Eita Kobayashi在2011年的ECRYPT轻量级密码会议上首次提出的，并发表在2012年的SAC会议上。它的分组长度是64比特，密钥长度有80比特和128比特两个版本，其采用广义的Feistel结构(Generalized Feistel Structure，简称GFS),并由36轮轮函数构成，这里我们重点介绍80位的算法。

1.1 加解密方式

1.1.1 加密

Twine-80的加密算法如下所示：
加密算法
该算法采用的是广义的Feistel结构，具体结构如下图所示：
Feistel结构
我们可以看出，此算法在Feistel结构的基础上改造了位置交换的方法，我们称之为π置换（π-1置换用于解密）：
π置换
Feistel结构中S盒如下表：S-box

void Feistel(int r,int k)
{int i;char a;if(k == 1){if(r != 35)for(i = 0;i < 16;i += 2){OutPut[PI[i]] = InPut[i];a = S[InPut[i] ^ R_Key[r][i / 2]];OutPut[PI[i + 1]] = InPut[i + 1] ^ a;}elsefor(i = 0;i < 16;i += 2){OutPut[i] = InPut[i];a = S[InPut[i] ^ R_Key[r][i / 2]];OutPut[i + 1] = InPut[i + 1] ^ a;}}else{if(r != 35)for(i = 0;i < 16;i += 2){OutPut[Pi[i]] = InPut[i];a = S[InPut[i] ^ R_Key[35 - r][i / 2]];OutPut[Pi[i + 1]] = InPut[i + 1] ^ a;}elsefor(i = 0;i < 16;i += 2){OutPut[i] = InPut[i];a = S[InPut[i] ^ R_Key[35 - r][i / 2]];OutPut[i + 1] = InPut[i + 1] ^ a;}}
}

1.1.2 密钥生成算法

Twine-80的密钥生成算法如下所示：
密钥生成算法
方便起见，我们将算法用图画出：
密钥生成算法
其中轮常数Con如下：在这里插入图片描述

void MakeRKey()
{int i,j,k;int choose[8] = {1,3,4,6,13,14,15,16};char ch,ConH,ConL;char key[20] = {0};for(i = 0;i < 10;i++){ch = fgetc(KEY);for(j = (2 * i) + 1;j >= 2 * i;j--){key[j] = ch & 0x0F;ch = ch >> 4;}}for(i = 0;i < 36;i++){for(j = 0;j < 8;j++)R_Key[i][j] = key[j];if(i < 35){key[1] = key[1] ^ S[key[0]];key[4] = key[4] ^ S[key[16]];ConL = CON[i] & 0x07;ConH = CON[i] >> 3;ConH = ConH & 0x07;key[7] = key[7] ^ ConH;key[19] = key[19] ^ ConL;ch = key[0];for(j = 0;j < 19;j++)key[j] = key[j + 1];key[j] = ch;for(k = 0;k < 3;k++){ch = key[0];for(j = 0;j < 18;j++)key[j] = key[j + 1];key[j] = ch;}}}
}

1.1.3 解密

由于轮函数的等价结构，解密算法与加密算法除π置换与轮密钥的注入顺序不同外，其余均相似。

1.1.4 全部代码

代码作用是将plaintext0.txt中的数据加密为ciphertext.txt，然后再解密为plaintext.txt：

#include<stdio.h>
#include<stdlib.h>
#include<string.h>FILE *KEY;
int flag;
int PI[16] = {5,0,1,4,7,12,3,8,13,6,9,2,15,10,11,14};
int Pi[16] = {1,2,11,6,3,0,9,4,7,10,13,14,5,8,15,12};
char S[16] = {0x0c,0x00,0x0f,0x0a,0x02,0x0b,0x09,0x05,0x08,0x03,0x0d,0x07,0x01,0x0e,0x06,0x04};
char CON[35] = {0x01,0x02,0x04,0x08,0x10,0x20,0x03,0x06,0x0c,0x18,0x30,0x23,0x05,0x0a,0x14,0x28,0x13,0x26,0x0f,0x1e,0x3c,0x3b,0x35,0x29,0x11,0x22,0x07,0x0e,0x1c,0x38,0x33,0x25,0x09,0x12,0x24};
char InPut[16] = {0},OutPut[16] = {0};
char R_Key[36][8] = {0};
char plain[16] = {0},cipher[16] = {0};void Read(FILE *OUT,int k)
{int i,j;char ch;for(i = 0;i < 8;i++){ch = fgetc(OUT);if(ch == -1){ch = 0;flag = 0;if(i == 0){flag = -1;return;}}for(j = (2 * i) + 1;j >= 2 * i;j--){if(k == 1)plain[j] = ch & 0x0F;elsecipher[j] = ch & 0x0F;ch = ch >> 4;}}
}void Write(FILE *IN,int k)
{int i,j;char ch;for(i = 0;i < 8;i++){ch = 0x00;for(j = 2 * i;j <= (2 * i) + 1;j++){ch = ch << 4;if(k == 1)ch =  ch | cipher[j];elsech =  ch | plain[j];}fputc(ch,IN);}
}void MakeRKey()
{int i,j,k;int choose[8] = {1,3,4,6,13,14,15,16};char ch,ConH,ConL;char key[20] = {0};for(i = 0;i < 10;i++){ch = fgetc(KEY);for(j = (2 * i) + 1;j >= 2 * i;j--){key[j] = ch & 0x0F;ch = ch >> 4;}}for(i = 0;i < 36;i++){for(j = 0;j < 8;j++)R_Key[i][j] = key[j];if(i < 35){key[1] = key[1] ^ S[key[0]];key[4] = key[4] ^ S[key[16]];ConL = CON[i] & 0x07;ConH = CON[i] >> 3;ConH = ConH & 0x07;key[7] = key[7] ^ ConH;key[19] = key[19] ^ ConL;ch = key[0];for(j = 0;j < 19;j++)key[j] = key[j + 1];key[j] = ch;for(k = 0;k < 3;k++){ch = key[0];for(j = 0;j < 18;j++)key[j] = key[j + 1];key[j] = ch;}}}
}void Feistel(int r,int k)
{int i;char a;if(k == 1){if(r != 35)for(i = 0;i < 16;i += 2){OutPut[PI[i]] = InPut[i];a = S[InPut[i] ^ R_Key[r][i / 2]];OutPut[PI[i + 1]] = InPut[i + 1] ^ a;}elsefor(i = 0;i < 16;i += 2){OutPut[i] = InPut[i];a = S[InPut[i] ^ R_Key[r][i / 2]];OutPut[i + 1] = InPut[i + 1] ^ a;}}else{if(r != 35)for(i = 0;i < 16;i += 2){OutPut[Pi[i]] = InPut[i];a = S[InPut[i] ^ R_Key[35 - r][i / 2]];OutPut[Pi[i + 1]] = InPut[i + 1] ^ a;}elsefor(i = 0;i < 16;i += 2){OutPut[i] = InPut[i];a = S[InPut[i] ^ R_Key[35 - r][i / 2]];OutPut[i + 1] = InPut[i + 1] ^ a;}}
}int main()
{int mode,i,r;FILE *M,*C;if((KEY = fopen("key.txt","rb")) == NULL){printf("\nkey.txt Fail,Close!");getchar();exit(1);}MakeRKey();while(1){flag = 1;printf("Plase choose:\n1. encrypt \n2. decrypt \n3. exit \n");scanf("%d",&mode);if(mode == 1){if((M = fopen("plaintext0.txt","rb")) == NULL){printf("\nplaintext.txt Fail,Close!");getchar();exit(1);}if((C = fopen("ciphertext.txt","wb")) == NULL){printf("\nciphertext.txt Fail,Close!");getchar();exit(1);}while(flag){Read(M,1);if(flag == -1)break;for(i = 0;i < 16;i++)InPut[i] = plain[i];for(r = 0;r < 36;r++){Feistel(r,1);for(i = 0;i < 16;i++)InPut[i] = OutPut[i];}for(i = 0;i < 16;i++)cipher[i] = OutPut[i];Write(C,1);}fclose(M);fclose(C); }if(mode == 2){if((C = fopen("ciphertext.txt","rb")) == NULL){printf("\nciphertext.txt Fail,Close!");getchar();exit(1);}if((M = fopen("plaintext.txt","wb")) == NULL){printf("\nplaintext.txt Fail,Close!");getchar();exit(1);}while(flag){Read(C,2);if(flag == -1)break;for(i = 0;i < 16;i++)InPut[i] = cipher[i];for(r = 0;r < 36;r++){Feistel(r,2);for(i = 0;i < 16;i++)InPut[i] = OutPut[i];}for(i = 0;i < 16;i++)plain[i] = OutPut[i];Write(M,2);}fclose(M);fclose(C); }if(mode == 3){fclose(KEY);exit(0);}system("pause");system("cls");}return 0;
}

1.2. 分组密码的模式

在数组密码中，如何将长的明文数据分成算法要求的长度也是一个问题。为此，人们提出了分组密码的分组模式：

1.2.1 ECB模式

加密：
在这里插入图片描述
解密：
在这里插入图片描述

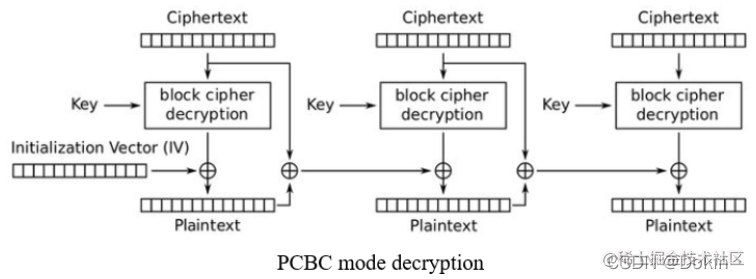
1.2.2 CBC模式

加密：
在这里插入图片描述
解密：
在这里插入图片描述

1.2.3 CFB模式

加密：
在这里插入图片描述
解密：
在这里插入图片描述

1.2.4 OFB模式

加密：
在这里插入图片描述
解密：
在这里插入图片描述

1.2.5 CTR模式

加密：
在这里插入图片描述
解密：
在这里插入图片描述

2.序列密码

序列密码也称为流密码（Stream Cipher），它是对称密码算法的一种。序列密码具有实现简单、便于硬件实施、加解密处理速度快、没有或只有有限的错误传播等特点，因此在实际应用中，特别是专用或机密机构中保持着优势，典型的应用领域包括无线通信、外交通信。
1949年Shannon证明了只有一次一密的密码体制是绝对安全的，这给序列密码技术的研究以强大的支持，序列密码方案的发展是模仿一次一密系统的尝试，或者说“一次一密”的密码方案是序列密码的雏形。如果序列密码所使用的是真正随机方式的、与消息流长度相同的密钥流，则此时的序列密码就是一次一密的密码体制。若能以一种方式产生一随机序列（密钥流），这一序列由密钥所确定，则利用这样的序列就可以进行加密，即将密钥、明文表示成连续的符号或二进制，对应地进行加密,加解密时一次处理明文中的一个或几个比特。
在序列密码中，密钥流由密钥流发生器f产生：zi=f(k,si)，这里的si是加密器中存储器（记忆元件）在i时刻的状态。根据加密器中的记忆元件si的存贮状态是否依赖于明文字符，序列密码可进一步分成同步和自同步两种。如果si独立于明文字符则称为同步流密码，否则称为自同步流密码。
序列密码算法主要依靠（线性）反馈移位寄存器，这里就不过多说明了。


http://chatgpt.dhexx.cn/article/Hd9LokgR.shtml

相关文章

中国商用密码算法SM4

中国商用密码算法SM4

中国商用密码算法SM4 2006年我国国家密码管理局公布了无线局域网产品使用的SM4密码算法。这是我国第一次公布自己的商用密码算法&#xff0c;意义重大&#xff0c;影响深远。这一举措标志着我国商用密码管理更加科学化和国际接轨。 SM4密码算法设计简洁&#xff0c;算法结构有…
阅读更多...
区块链的密码算法

区块链的密码算法

区块链系统包含了计算机科学过去几十年的成果&#xff1a;计算机网络P2P、算法、数据库、分布式系统、计算机密码学等 密码学是区块链系统安全性保障的基础技术&#xff0c;形象地称为区块链的骨骼 哈希算法 ■哈希算法(Hash、 散列、杂凑&#xff0c; 消息摘要&#xff0c;…
阅读更多...
8、RSA 公钥密码算法

8、RSA 公钥密码算法

目录 RSA公钥密码算法 一、RSA的数学基础 二、RSA原理 三、算法详细流程 四、RSA特点 五、RSA应用 参考推荐&#xff1a; https://blog.csdn.net/lemon_tree12138/article/details/50696926 RSA加密算法原理_张维鹏的博客-CSDN博客_rsa加密算法原理 图解RSA算法取余和…
阅读更多...
常用的密码算法有哪些？

常用的密码算法有哪些？

我们将密码算法分为两大类。 对称密码&#xff08;密钥密码&#xff09;——算法只有一个密钥。如果多个参与者都知道该密钥&#xff0c;该密钥 也称为共享密钥。非对称密码&#xff08;公钥密码&#xff09;——参与者对密钥的可见性是非对称的。例如&#xff0c;一些参与者仅…
阅读更多...
分组密码算法与DES算法

分组密码算法与DES算法

目录 1 分组密码的含义 1.1 分组密码介绍 1.2 分组密码的含义 1.3 分组密码的要求 2 分组密码的设计思想 2.1 分组密码的设计思想 3 分组密码的基本特点 3.1 分组密码的基本特点 3.2 分组密码的迭代结构 3.3 子密钥的生成方法 3.4 轮函数的设计准则 3.5 迭代的轮数 4…
阅读更多...
11、国产密码算法

11、国产密码算法

参考推荐&#xff1a; 国密SM1\ SM2\ SM3\ SM4\ SSF33算法和国际RSA算法的对应关系_小明做IT的博客-CSDN博客_ssf33算法 国密算法SM1/SM2/SM3/SM4_fengwang0301的博客-CSDN博客_sm2/sm3/sm4 国产密码算法 国产密码算法是指由国家密码研究相关机构自主研发&#xff0c;具有相…
阅读更多...
密码算法应用规范

密码算法应用规范

术语解释 对称算法&#xff08;Symmetric key algorithm&#xff09;&#xff1a;采用相同的密钥执行加密或解密。 非对称算法&#xff08;Asymmertric key algorithm&#xff0c;公开密钥算法&#xff09;&#xff1a;用作加密的密钥不同于用作解密的密钥&#xff0c;而且解密…
阅读更多...
古典密码算法(移位密码算法、维吉尼亚算法)

古典密码算法(移位密码算法、维吉尼亚算法)

古典密码算法(凯撒、维吉尼亚) A. 1-1.移位密码算法 【实验目的】 1&#xff09; 学习移位密码的原理 2&#xff09; 学习移密码的实现 【实验原理】 算法原理 a) 移位密码就是对26个字母进行移位操作&#xff0c;可以移动任意位数&#xff0c;这样就实现了对明文的加密…
阅读更多...
换位密码算法

换位密码算法

换位密码算法基本原理&#xff1a;先把明文按固定长度进行分组&#xff0c;然后对每一组的字符进行换位操作&#xff0c;从而实现加密。为加强安全性&#xff0c;可进行多次换位密码算法运算。 import random def encrypt(plainText,t):result[]lengthlen(t)temp[plainText[i:…
阅读更多...
常见密码学算法

常见密码学算法

学习笔记 分类 密码学用于解决信息安全中的保密性&#xff0c;完整性&#xff0c;认证和不可否认性等问题。最初主要用于解决保密性。随着密码学技术的发展&#xff0c;逐渐应用到其它领域。 常见密码学算法&#xff1a;DES,AES; RSA, ECC; Hash; Signature等。 分类 对称密…
阅读更多...
密码学基础（一）常见密码算法分类

密码学基础（一）常见密码算法分类

一、密码算法分类&#xff1a; 密码算法主要分为三类&#xff1a;对称密码算法、 非对称密码算法、摘要算法。 二、对称密码算法&#xff08;Symmetric-key Algorithm&#xff09; 1、概念 对称加密(也叫私钥加密)指加密和解密使用相同密钥的加密算法。有时又叫传统密码算…
阅读更多...
常用的密码算法汇总分析（动态更新ing）

常用的密码算法汇总分析（动态更新ing）

常用密码算法整理汇总 常用对称加密算法常用非对称加密算法常用Hash算法国产密码关于密码算法会持续更新.... 常用对称加密算法 对称加密算法(分组加密)描述DES将明文分为64位一组、密钥64位&#xff0c;实际56位&#xff08;64位中8位奇偶校验位&#xff09;3DES执行了3次DES&…
阅读更多...
【密码学】常见密码算法分类和运用

【密码学】常见密码算法分类和运用

一、摘要算法&#xff08;Digest Algorithm&#xff09; 摘要算法 是指把任意长度的输入消息数据转化为固定长度的输出数据的一种密码算法&#xff0c;又称为 散列函数 、 哈希函数 、 杂凑函数 、单向函数 等&#xff0c;通常用来做数据完整性的判定&#xff0c;即对数据进行…
阅读更多...
常用密码算法介绍

常用密码算法介绍

算法种类 根据技术特征&#xff0c;现代密码学可分为三类&#xff1a; 对称算法 说明&#xff1a;加密密钥和解密密钥相同&#xff0c;对明文、密文长度没有限制 子算法&#xff1a; 流密码算法&#xff1a;每次加密或解密一位或一字节的明文或密文 分组密码算法&#xff…
阅读更多...
2020 shodan 配置详解

2020 shodan 配置详解

需要先注册一个号>然后才能在kali里安装并认证 官网&#xff1a;https://www.shodan.io 安装命令&#xff1a; git clone https://github.com/achillean/shodan-python.git cd shodan-python python setup.py installshodan -h 查看使用&#xff1a; 这个。。土味英语&am…
阅读更多...
Python中shodan模块的使用

Python中shodan模块的使用

关于shodan的安装和使用&#xff0c;传送门——> 渗透测试之Shodan的安装和使用 常用 Shodan 库函数 shodan.Shodan(key) &#xff1a;初始化连接APIShodan.count(query, facetsNone)&#xff1a;返回查询结果数量Shodan.host(ip, historyFalse)&#xff1a;返回一个IP的详细…
阅读更多...
暗黑引擎 -- Shodan常用搜索语法

暗黑引擎 -- Shodan常用搜索语法

fofa&#xff0c;钟馗之眼&#xff0c;shodan等等一系列的公网设备搜索引擎&#xff0c;其中fofa和shodan使用的最多&#xff0c;本文就来整理一些shodan的搜索语法 Shodan&#xff1a;www.shodan.io Ps&#xff1a;均来自互联网搜集整理 工业控制系统 三星电子广告牌 &quo…
阅读更多...
shodan的使用及maltego的注册

shodan的使用及maltego的注册

渗透学习 信息收集工具指南1 文章目录 渗透学习前言*本文只做学习用途&#xff0c;严禁利用本文提到的技术进行非法攻击&#xff0c;否则后果自负&#xff0c;本人不承担任何责任。* 一、shodan1.网络空间搜索引擎2.shodan3.命令行shodan 二、maltego1.情报分析2.maltego 总结…
阅读更多...
shodan命令行

shodan命令行

shodan获取IP信息 kali中命令行输入 shodan host ip 可以看到好多&#xff0c;比如可能漏洞&#xff0c;开放端口&#xff0c;运行的服务 shodan info 查询账户信息 Shodan获取自身外部IP shodan myip shodan检测是否有蜜罐保护 shodan honeyscore ip 蜜罐好比是情报收…
阅读更多...
使用shodan/censys API搜索免费的elasticsearch/kibana资源

使用shodan/censys API搜索免费的elasticsearch/kibana资源

文章目录 注册shodan并获取API安装shodan注册censys并获取API安装censys用censys查询可用elasticsearch资源 记得以前我在elastic社区分享过一个主题《ITDS如何玩转elastic》(这里的ITDS是IT屌丝的意思)&#xff0c;里面提到过如何用elasticsearch做数字货币的交易数据分析&…
阅读更多...
推荐文章

Copyright @ 2022~2023