1. 基本概念

动态规划通过拆分问题，将问题拆分成许多的子问题，定义问题状态和状态之间的关系（即状态转移方程或递推公式），使得问题能够以递推（或者说分治）的方式去解决。按顺序求解子问题，前一子问题的解，为后一子问题的求解提供了有用的信息，在求解任一子问题时，列出各种可能的局部解，通过决策保留那些有可能达到最优的局部解，丢弃其他局部解。依次解决各子问题，最后一个子问题就是初始问题的解。 [2] 。

1.1 动态规划和递归之间的关系

动态规划本质上就是递归，动态规划通过将问题划分为若干个子问题，通过递推关系，一步一步求得最终问题的关系。但是子问题之间可能会有重复，因此如果单纯的使用递归方法来实现动态规划问题时间复杂度会比较高。
但是，一般能用递归解决的问题都可以转化为用动态规划解决。

以斐波那契数列为例：

其递归代码为：

def fiboSeq(n):if n <= 1:return nelse:return (fiboSeq(n - 1) + fiboSeq(n - 2))

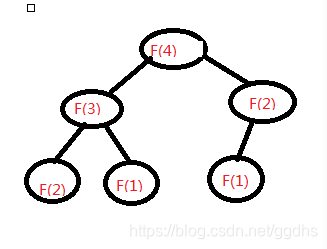
可以看出，传统的递归是从上向下的计算，某些子问题会被重复计算，如在计算第四项裴波那契数列时，F（2）倍计算了2次。其时间复杂度为o（2^n）

添加备忘录的写法(还是从上到下）：

由于传统的递归写法，会重复计算某一些子问题，为了解决这些问题，我们可以提前申请一个数组，用来记录计算过的子问题，当递归的时候，就不用再重复计算某些子问题了。其时间复杂度和空间复杂度均为O(n)。

def fiboSeq(n):if n < 0:return 0memories = [-1 for i in range(n + 1)]if n == 0:memories[n] = 0return 0if n == 1:memories[n] = 1return 1if n == 2:memories[n] = 1return 1if memories[n] != -1:return memories[n]else:memories[n] = fiboSeq(n-1) + fiboSeq(n-2)return memories[n]

从下到上（借助辅助数组）（动态规划）：

从f(1)开始算，逐步计算出f(2),……,f(n)。由于接住了一个辅助数组，时间复杂度为o（n），空间复杂度为o（n）

def fiboSeq(n):if n < 0:return 0if n <= 1:return nif n == 2:return 1arr = [0,1,1]for i in range(3,n+1):arr.append(arr[i-1]+arr[i-2])return arr[n]

从下到上（不借助辅助数组）：

通过上面的代码可以看出，每次参与循环的只有 i，i-1 , i-2三项，因此该方法的空间可以进一步的压缩如下，空间复杂度为o（1）。

def fiboSeq(n):if n < 0:return 0if n <= 1:return nif n == 2:return 1memories_2 = 1memories_1 = 1for i in range(3,n+1):memories_0 = memories_1 + memories_2memories_2 = memories_1memories_1 = memories_0return memories_0

前两种利用递归的方法是从要求解的第n项裴波那契数列开始，逐步向下求解子问题，然后再一步步返回，求得最终的结果。
后两种动态规划方法是从第一项裴波那契数列开始，通过前面子问题的解，来得到后面子问题的解。
动态规划可以把递归的指数复杂度提高到线性复杂度。

2. 动态规划适用情况

（1）最优化原理：如果问题的最优解所包含的子问题的解也是最优的，就称该问题具有最优子结构，即满足最优化原理。最优子结构应可以理解为大问题可以不断的分解为小问题，通过每个小问题的最优解可以得到相应大问题的最优解。
（2）无后效性：即某阶段状态（最优解）一旦确定，就不受这个状态以后决策的影响。也就是说，某状态以后的过程不会影响以前的状态，只与当前状态有关。
（3）有重叠子问题：即子问题之间是不独立的，一个子问题在下一阶段决策中可能被多次使用到。就比如前面的裴波那契数列的递归算法，进行一次递归f（1）就被计算一次，因此裴波那契数列可以利用动态规划的方法进行求解。（该性质并不是动态规划适用的必要条件，但是如果没有这条性质，动态规划算法同其他算法相比就不具备优势，在动态规划算法中使用数组来保存子问题的解，这样子问题多次求解的时候可以直接查表不用调用函数递归。）

3. 动态规划的步骤

动态规划所处理的问题是一个多阶段决策问题，一般由初始状态开始，通过对中间阶段决策的选择，达到结束状态。这些决策形成了一个决策序列，同时确定了完成整个过程的一条活动路线(通常是求最优的活动路线)。如图所示。动态规划的设计都有着一定的模式，一般要经历以下几个步骤，如下图所示：
初始状态→│决策1│→│决策2│→…→│决策n│→结束状态
(1)划分阶段：按照问题的时间或空间特征，把问题分为若干个阶段。在划分阶段时，注意划分后的阶段一定要是有序的或者是可排序的，即前后有所关联，否则问题就无法求解。
(2)确定状态和状态变量：将问题发展到各个阶段时所处于的各种客观情况用不同的状态表示出来。当然，状态的选择要满足无后效性。
(3)确定决策并写出状态转移方程：因为决策和状态转移有着天然的联系，状态转移就是根据上一阶段的状态和决策来导出本阶段的状态。所以如果确定了决策，状态转移方程也就可写出。但事实上常常是反过来做，根据相邻两个阶段的状态之间的关系（状态转移方程）来确定决策，即当前子问题的最优解是什么。
(4)寻找边界条件：给出的状态转移方程是一个递推式，需要一个递推的终止条件或边界条件。
一般，只要解决问题的阶段、状态和状态转移决策确定了，就可以写出状态转移方程（包括边界条件）。实际应用中可以按以下几个简化的步骤进行设计：
（1）分析最优解的性质，并刻画其结构特征。
（2）递归的定义最优解。
（3）以自底向上或自顶向下的记忆化方式（备忘录法）计算出最优值。
（4）根据计算最优值时得到的信息，构造问题的最优解。

ps：备忘录通常有两种：

线性模型：数组存储各个子问题的最优解，如小朋友过桥
区间模型：矩阵存储各个子问题的最优解，如背包问题，不过背包问题也可以进行空间优化，成为线性模型。