一、函数说明
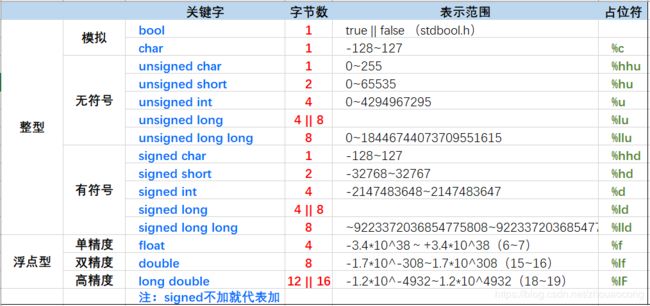
对 double 而言,取整、取余的相关函数和运算符请参考下表:
VB6.0 | C | C# | 说 明 |
Int(x) | floor(x) | Math.Floor(x) | floor表示地板,也就是将 Math.Floor(1.9) 返回 1 Math.Floor(1.0) 返回 1 Math.Floor(-1.0) 返回 -1 Math.Floor(-1.3) 返回 -2 Math.Floor(-1.9) 返回 -2 |
ceil(x) | Math.Ceiling(x) | ceil表示天花板,也就是将 Math.Ceiling(1.9) 返回 2 Math.Ceiling(1.3) 返回 2 Math.Ceiling(1.0) 返回 1 Math.Ceiling(-1.0) 返回 -1 Math.Ceiling(-1.9) 返回 -1 | |
Fix(x) | Math.Truncate(x) | 表示取 Math.Truncate(1.9) 返回 1 Math.Truncate(1.0) 返回 1 Math.Truncate(-1.0) 返回 -1 Math.Truncate(-1.9) 返回 -1 | |
Round(x) | Math.Round(x,...) | 表示四舍五入,如:四舍五入取整 Math.Round(1.9) 返回 2 Math.Round(1.5) 返回 2 Math.Round(1.3) 返回 1 Math.Round(1.0) 返回 1 Math.Round(-1.0) 返回 -1 Math.Round(-1.3) 返回 -1 Math.Round(-1.5) 返回 -2 Math.Round(-1.9) 返回 -2 | |
x Mod y | fmod(x,y) | x % y | 返回 x / y 的余数,其符号与 x 一致。 C语言里 % 只能用于整型变量 注意:VB6.0会对结果四舍五入取整 |
x / y | x / y | x / y | 返回 x / y,对于整数而言,将舍去小数部分。 |
1、详述Math.Round
Math.Round 还有更丰富的功能
①精确到小数点后n位
如:Math.Round(x,n) 表示对 x 只取小数点后 n 位,多余部分四舍五入。
②四舍五入问题
四舍是一定的,但对于五到底入还是不入呢?Math.Round是可以通过MidpointRounding来进行控制的。
MidpointRounding.AwayFromZero 表示五入,这是默认的方法,如:
Math.Round(1.5,MidpointRounding.AwayFromZero); 返回 2
Math.Round(-1.5,MidpointRounding.AwayFromZero); 返回 -2
MidpointRounding.ToEven 就比较有意思了,如果5前面的数字是奇数则入,否则就舍去。如:
Math.Round(2.5,MidpointRounding.ToEven); 返回 2
Math.Round(1.5,MidpointRounding.ToEven); 返回 2
Math.Round(-1.5,MidpointRounding.ToEven); 返回 -2
Math.Round(-2.5,MidpointRounding.ToEven); 返回 -2
二、函数关系
1、floor和ceil的关系
floor(x) = -ceil(-x),同样的ceil(x)=-floor(-x)。VB6.0里没有ceil函数,就可以用 -Int(-x) 来代替。
2、Math.Truncate 和floor、ceil的关系
Math.Truncate(x) = 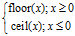
写成C语言代码就是
double Truncate(double x)
{
if(x >= 0.0)
{
return floor(x);
}
return ceil(x); //或-floor(-x)
}
三、应用
1、归化角度
如:手表的秒针1分钟走1圈。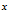
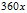
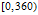
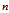
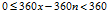
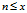
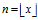
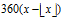
同样的,判断经度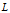
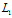
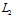
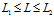
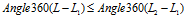
函数Angle360(x)将返回角度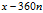
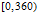
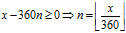
double Angle360(double x)
{
return x - floor(x / 360.0) * 360.0;
}
2、扩展fmod函数
上述问题里,将角度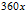
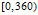
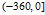
fmod(x,y)的实质是找到合适的整数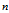
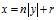
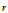
如果需要余数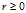
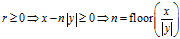
如果需要余数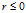
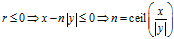
如果需要求绝对值最小的余数,则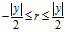
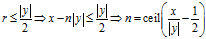
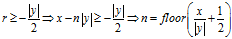
fmod函数的模拟代码如下
double fmod(double x,double y)
{
y = fabs(y);
if(x >= 0.0)
{
y = x - y * floor(x / y);
}
else
{
y = x - y * ceil(x / y);
}
return y;
}
fmod函数的扩展代码如下
/****************************************************************\
求 x / y 的余数
nFlag [in] 1 返回的余数大于等于零
-1 返回的余数小于等于零
2 返回绝对值最小的余数,若同时出现 ±(y / 2) 则取正值
-2 返回绝对值最小的余数,若同时出现 ±(y / 2) 则取负值
0 与 2 相同
\****************************************************************/
double fmodEx(double x,double y,int nFlag)
{
y = fabs(y);
if(nFlag < -2)
{
nFlag = -2;
}
else if(nFlag > 2)
{
nFlag = 2;
}
switch(nFlag)
{
case 1://返回的余数大于等于 0
y = x - y * floor(x / y);
break;
case -1://返回的余数小于等于 0
y = x - y * ceil(x / y);
break;
case -2://返回的绝对值最小的余数,优先考虑 - y / 2
y = x - y * floor(x / y + 0.5);
break;
default://返回的绝对值最小的余数,优先考虑 + y / 2
y = x - y * ceil(x / y - 0.5);
break;
}
return y;
}
3、格点
现在要在区间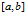

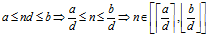
计算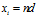
double n0 = ceil(a/d);
double x0 = n0 * d;
int nMax = (int)(floor(b/d) - n0 + 0.1);
double x;
for(int i = 0;i <= nMax;i++)
{
x = x0 + i * d;
}
下面的函数专门用来获取格点
/**********************************************************\
获取区间[a,b]之间的格点,格点坐标是 d 的整数倍
x0 [out] 返回起始格点。
若 d 大于零,x0 是坐标最小的格点
若 d 小于零,x0 是坐标最大的格点
返回:获得格点的个数 nCount
格点坐标为 x0 + n * d。n = 0,1,2,...nCount - 1
\**********************************************************/
long GetLatticePoints(double a,double b,double d,double*x0)
{
long nCount = 0; //格点个数
double nMin; //n 的最小值
double nMax; //n 的最大值
a /= d;
b /= d;
if(a > b)
{
double t;
t = a;
a = b;
b = t;
}
nMin = ceil(a);
nMax = floor(b);
if(nMax >= nMin)
{
nCount = (long)(nMax - nMin + 1.1);
if(x0)
{
*x0 = nMin * d;
}
}
return nCount;
}
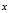 向下取整数,即返回最大的整数
向下取整数,即返回最大的整数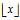 使得
使得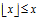
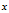 向上取整数,即返回最小的整数
向上取整数,即返回最小的整数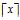 使得
使得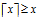
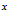 的整数部分
的整数部分