A. Casimir’s String Solitaire
给定一个只存在ABC的字符串，一次操作可以同时删除任意位置的‘A’和‘B’或‘B’和‘C’，问能否删完。
只需判断B的数量是否等于A+C的数量。

#include<bits/stdc++.h>
using namespace std;#define read(a) scanf("%d",&a)
#define maxn 50int main() {int T;read(T);while(T--) {string a;cin>>a;int b[4]={0};for(int i=0;i<a.size();i++) {if(a[i]=='A') b[1]++;else if (a[i]=='B') b[2]++;else b[3]++;}if(b[2]==b[1]+b[3]) printf("YES\n");else printf("NO\n");}return 0;
}

B. Shifting Sort
给定一个长度为n的数列，一次操作可以选择一个子串，将子串进行任意长度的滚动。
要求输出一个方案，在n次操作内使该数列递增。
由于不需要找出最小操作数，所以只需要每次操作把当前最小的数移动到合理的位置即可。

#include<bits/stdc++.h>
using namespace std;#define read(a) scanf("%d",&a)
#define maxn 50struct ans{int l,r,d;ans(){}ans(int ll,int rr,int dd) {l=ll,r=rr,d=dd;}
};int a[maxn+5],b[maxn+5],c[maxn+5];
vector<ans> s;int main() {int T;read(T);while(T--) {int n;read(n);for(int i=1;i<=n;i++) read(a[i]),b[i]=a[i];sort(b+1,b+n+1);s.clear();		for(int i=1;i<n;i++) {int t;if(a[i]==b[i]) continue;for(int j=i;j<=n;j++) {if(a[j]==b[i]) {t=j;break;}}memset(c,0,sizeof(c));memcpy(c+1,a+1,(i-1)*sizeof(int));memcpy(c+i,a+t,(n-t+1)*sizeof(int));memcpy(c+i+n-t+1,a+i,(t-i)*sizeof(int));memcpy(a+1,c+1,n*sizeof(int));s.push_back(ans(i,n,t-i));}printf("%d\n",s.size());for(int i=0;i<s.size();i++) {printf("%d %d %d\n",s[i].l,s[i].r,s[i].d);}}return 0;
}

C. Ticks

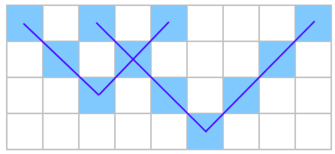
给一个只有黑白n*m的棋盘，问能不能完全由大于k的勾组成。
遍历枚举勾勾的最下端，暴力统计。

#include<bits/stdc++.h>
using namespace std;#define read(a) scanf("%d",&a)
#define maxn 20
#define readc(a) do{scanf("%c",&a);}while(a!='.'&&a!='*')int n,m,K;
bool a[maxn+5][maxn+5],b[maxn+5][maxn+5];int main() {int T;read(T);while(T--) {read(n),read(m),read(K);memset(a,0,sizeof(a));for(int i=1; i<=n; i++)for(int j=1; j<=m; j++) {char t;readc(t);if(t=='.') a[i][j]=0;else a[i][j]=1;}memcpy(b,a,sizeof(a));for(int i=1; i<=n; i++) {for(int j=1; j<=m; j++) {int k=0;for( ; ; ) {if(!a[i-k][j-k]||!a[i-k][j+k]) break;k++;}if(k>K) {while(k--) b[i-k][j-k]=b[i-k][j+k]=0;}}}bool ans=1;for(int i=1; i<=n; i++) {for(int j=1; j<=m; j++) {if(b[i][j]) {ans=0;break;}}}if(ans) printf("YES\n");else printf("NO\n");}return 0;
}

D. Productive Meeting
有n个数，一次操作可以让任意两个数大于0的数-1，问最后无法操作时剩下数的最小值。
每次选出当前最大的两个数进行操作，可以用优先队列（大根堆）维护。

#include<bits/stdc++.h>
using namespace std;#define read(a) scanf("%d",&a)
#define maxn (int)2e5struct Pair {int x,y;Pair() {}Pair(int xx,int yy) {x=xx,y=yy;}
};struct ele {int x,pos;ele() {}ele(int xx,int pp) {x=xx,pos=pp;}bool operator < (const ele& e) const {return x<e.x;}
};int n;
priority_queue<ele> a;
vector<Pair> b;int main() {int T;read(T);while(T--) {b.clear();while(a.size()) a.pop();read(n);for(int i=1; i<=n; i++) {int x;read(x);if(x!=0) a.push(ele(x,i));}while(a.size()>1) {ele x1=a.top();a.pop();ele x2=a.top();a.pop();b.push_back(Pair(x1.pos,x2.pos));x1.x--,x2.x--;if(x1.x!=0) a.push(x1); if(x2.x!=0) a.push(x2); }printf("%d\n",b.size());for(int i=0;i<b.size();i++) {printf("%d %d\n",b[i].x,b[i].y);}}return 0;
}

E1. Permutation Minimization by Deque
给一个数列，需要按顺序把数列中的数插入双端队列中（可以是头部和尾部），使最后队列中的数字典序最小。
贪心，比当前头大的往尾部插，小或等于的往队首插。

#include<bits/stdc++.h>
using namespace std;#define read(a) scanf("%d",&a)
#define maxn (int)2e5int a[maxn+5];
deque<int> q;int main() {int T;read(T);while(T--) {int n;read(n);for(int i=1;i<=n;i++) read(a[i]);q.clear();for(int i=1;i<=n;i++) {if(a[i]<q.front()) q.push_front(a[i]);else q.push_back(a[i]);}for(int i=1;i<=n;i++) {printf("%d ",q.front());q.pop_front();}printf("\n");}return 0;
}

E2. Array Optimization by Deque
给一个数列，需要按顺序把数列中的数插入双端队列中（可以是头部和尾部），使最后队列中的逆序对最少。
贪心，插入一个数的时候分别查询插在头部和尾部新增的逆序对数，选新增少的地方插。
查询操作用树状数组维护。

#include<bits/stdc++.h>
using namespace std;#define read(a) scanf("%d",&a)
#define maxn (int)4e5
#define ll long longstruct Pair{int x,num;Pair() {}Pair(int xx,int nn) {x=xx,num=nn;}bool operator < (const Pair& e) const {return x<e.x;}
};int n;
Pair a[maxn+5];
int b[maxn+5],c[maxn+5];int lowbit(int x) {return x&-x;
} void add(int x) {while(x<=n) {c[x]++;x+=lowbit(x);}
}int query(int x) {int ans=0;while(x>0) {ans+=c[x];x-=lowbit(x);}return ans;
}int main() {int T;read(T);while(T--) {read(n);for(int i=1;i<=n;i++) read(a[i].x),a[i].num=i; sort(a+1,a+1+n);int cnt=0;a[0].x=(1e9)+1,memset(c,0,sizeof(c));for(int i=1;i<=n;i++) {if(a[i].x!=a[i-1].x) ++cnt;b[a[i].num]=cnt;}ll ans=0;for(int i=1;i<=n;i++) {int s=query(b[i]-1),r=i-1-query(b[i]);if(r>s) ans+=s;else ans+=r;add(b[i]);}printf("%lld\n",ans);}return 0;
}

F. Array Stabilization (AND version)
给一个01数列，常数d，一次操作可以将数列滚动d个单位，并与原数列进行与操作。
问滚动多少次可以将数列变为全0。
一次操作即把每个位和后面d位（滚动意义上）与一遍，所以把每位和后d位建边，跑最短路，退出条件是走到一个为0的点。

#include<bits/stdc++.h>
using namespace std;#define read(a) scanf("%d",&a)
#define maxn (int)1e6 
#define ll long longstruct Pair{int x,y;Pair() {}Pair(int xx,int yy) {x=xx,y=yy;}bool operator < (const Pair& e) const {return x<e.x;}
};int n,d;
bool a[maxn+5],use[maxn+5];
int cnt;queue<Pair> que;int spfa() {int ans=0;while(!que.empty()) {int x=que.front().x,y=que.front().y;que.pop();int z=(x+d)%n;if(use[z]) continue;use[z]=1,++cnt;que.push(Pair(z,y+1));ans=max(ans,y+1);}if(cnt<n) return -1;else return ans;
}int main() {int T;read(T);while(T--) {memset(use,0,sizeof(use));cnt=0;read(n),read(d);for(int i=0;i<n;i++) {read(a[i]);if(!a[i]) que.push(Pair(i,0)),use[i]=1,++cnt;}int ans=spfa();printf("%d\n",ans);}return 0;
}

G. Minimal Coverage
有n根长度为a[n]的棍，现需将他们排成一根直线，使每根棍的两端分别与前一根和后一根的端点重合，求这样铺的最小长度。
看了题解。
dp[i][j]表示第i根棍，铺完后末端离最左端为j时，铺过的长度。
这里始终保持最左边为0，所以左端超过0时需要整体右移。

#include<bits/stdc++.h>
using namespace std;#define read(a) scanf("%d",&a)
#define maxn (int)1e4
#define maxm (int)2e3 
#define ll long longstruct Pair{int x,y;Pair() {}Pair(int xx,int yy) {x=xx,y=yy;}bool operator < (const Pair& e) const {return x<e.x;}
};int n;
int a[maxn+5];
int dp[maxn+5][maxm*2+5];int main() {int T;read(T);while(T--) {read(n);for(int i=1;i<=n;i++) read(a[i]);for(int i=0;i<=n;i++) for(int j=0;j<=maxm*2;j++) dp[i][j]=(int)1e9;dp[0][0]=0;for(int i=1;i<=n;i++) {for(int j=0;j<=maxm*2;j++) {if(j+a[i]<=maxm*2) {int x=max(dp[i-1][j],j+a[i]);dp[i][j+a[i]]=min(dp[i][j+a[i]],x);}if(j-a[i]>=0) {dp[i][j-a[i]]=min(dp[i][j-a[i]],dp[i-1][j]);} else {dp[i][0]=min(dp[i][0],dp[i-1][j]+a[i]-j);}}}int ans=(int)1e9;for(int i=0;i<=maxm*2;i++) ans=min(ans,dp[n][i]);printf("%d\n",ans);}return 0;
}