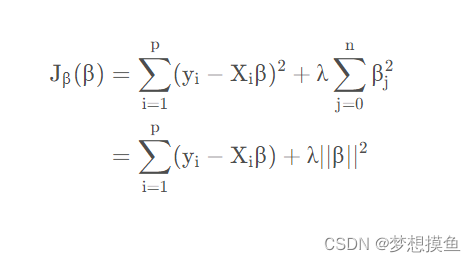多元线性回归改进 – 潘登同学的Machine Learning笔记

(简单回顾)多元线性回归模型

• 总目标：预测

• 模型：
  $$y={\beta }_0+{\beta }_1{x}_1+\cdots +{\beta }_k{x}_k$$

• 优化目标：MSE
  $$Loss=\sum _{n=1}^{m}erro{r}^2=\sum _{n=1}^m(\hat{y}-y{)}^2$$

• 优化方法:梯度下降法
  $${\theta }_j^{t+1}={\theta }_j^t-\eta \bullet gradien{t}_j$$

归一化normalization

• 一个问题:

如果现在多元线性回归中有两个x, 分别代表$x_1$土地价格和$x_2$中长期贷款利率, y表示房价水平;我们知道利率水平都是以5.1%这样的百分数形式出现的, 而土地价格动辄百万;

根据经济学的直觉, 在多元线性回归中${\theta }_1$肯定要比${\theta }_2$小得多, 不然因为$x_1$的量级远超过$x_2$，房价就由土地价格完全决定了;

再看回我们的梯度下降算法:
$$\begin{array}{rl}{\theta }_j^{t+1}& ={\theta }_j^t-\eta \bullet gradien{t}_j\\ g_j& =({\theta }^{T}X-Y)x_j\end{array}$$

仔细揣摩上式,可以发现梯度下降法其实是受两个因素影响的:

• $\theta$距$\hat{\theta }$的距离, 也就是距要求的$\theta$的距离;
• $gradient$的大小;

可以观察到$g_j$的大小其实是收到$x_j$影响的, 而量纲大的土地价格$gradien{t}_1$就会大, 走的就快；而碰巧量纲大的${\theta }_1$又比较小, 假设起点都是0, 在这两个因素的共同作用下,${\theta }_1$能更快的收敛;

所以我们需要消除量纲, 消除量纲这种事情其实在数据统计分析里面也经常做, 目的其实差不太多,我们只是用梯度下降的视角去解释了一下；

归一化的方法

• 最大值最小值归一化
  $$X_{i,j}^{\ast }=\frac{X_{i,j}-X_j^{min}}{X_j^{max}-X_j^{min}}$$
  注意:如果数据中有离群值, 即一个很大的$X_{k1}$那么整列$X_1$数据都会变得非常接近0,而只有一个1, 这样数据就失去了意义, 这种方法不好;

• 标准归一化
  $$X_{i,j}^{\ast }=\frac{X_{i,j}-X_j^{mean}}{X_j^{std}}$$
  注意:标准归一化并不能将数据缩放到0-1之间, 但是他能显著增加梯度下降法的速度;

回到梯度下降法

$$\left(\begin{array}{c}{\theta }_0^{t+1}\\ {\theta }_1^{t+1}\\ {\theta }_2^{t+1}\end{array}\right)=\left(\begin{array}{c}{\theta }_0^t\\ {\theta }_1^t\\ {\theta }_2^t\end{array}\right)-\eta ({\theta }^{T}X-Y)\left(\begin{array}{c}{X}_0\\ X_1\\ X_2\end{array}\right)$$
考虑下面的情形:

对所有的$\theta$而言, $\eta ({\theta }^{T}X-Y)$是共用的, 要是所有的数据维度,都是正数的话, 那么$\theta$在每一次梯度下降中更新的方向都是一样的(同增同减)

像下图所示,要想从 wt 更新到 w* 就必然要么 W1 和 W2 同时变大再同时变小，或者就 W1 和 W2 同时变小再同时变大。不能走蓝色的最优解路径，即 W1 变小的时候 W2 变大。(机器学习中的模型其实就是参数, 说训练模型,其实就是调整参数, 参数用$\theta$或W来表示都可以)

• 问题:怎么能让 W1 变小的时候 W2 变大呢？

改变数据的符号就可以啦！让X中的数有正有负就能实现蓝色路径这样的;而标准归一化减去均值的操作就能到达目的!!!

来个小例子试一试？

#%%归一化
from sklearn.preprocessing import MinMaxScaler,StandardScaler
import numpy as np
scaler = MinMaxScaler()
temp = np.arange(5)
print('最大值最小值归一化...')
print(scaler.fit_transform(temp.reshape(-1,1)))  #先摆成列再做归一化scaler1 = StandardScaler()
print('均值归一化...')
print(scaler1.fit_transform(temp.reshape(-1,1)))
# 打印结果
print('均值为:', scaler1.mean_)
print('标准差为:',scaler1.var_)

正则化regularization

• 过拟合和欠拟合

(1) under fit：还没有拟合到位，训练集和测试集的准确率都还没有到达最高。学的还不到位

(2) over fit：拟合过度，训练集的准确率升高的同时，测试集的准确率反而降低。学的过 度了，做过的卷子都能再次答对，考试碰到新的没见过的题就考不好。

(3) just right：过拟合前训练集和测试集准确率都达到最高时刻。学习并不需要花费很多 时间，理解的很好，考试的时候可以很好的把知识举一反三。真正工作中我们是奔着过 拟合的状态去调的，但是最后要的模型肯定是没有过拟合的

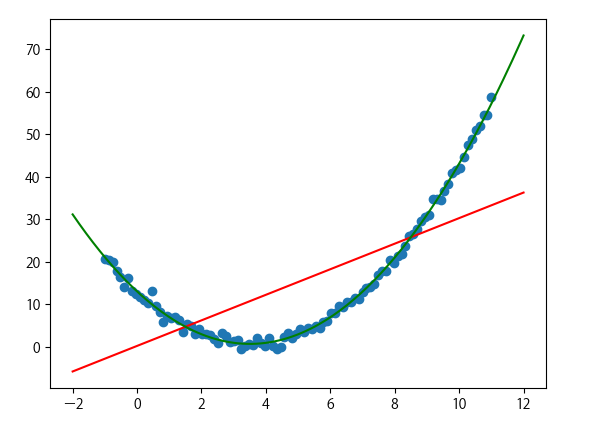
如下图, (1)表示欠拟合, (2)表示过拟合, (3)表示刚刚好:

• 鲁棒性Robust

正则化就是防止过拟合,增加模型的鲁棒性 robust,鲁棒是 Robust 的音译,也就是强壮的意思。就像计算机软件在面临攻击、网络过载等情况下能够不死机不崩溃,这就是该软件的鲁棒性。鲁棒性调优就是让模型拥有更好的鲁棒性,也就是让模型的泛化能力和推广能力更加的强大。

而对于MLR模型来说, 当X有波动的时候, 对于预测结果并没有什么影响, 那这个模型的鲁棒性就比较好了;

所以正则化（鲁棒性调优）的本质就是牺牲模型在训练集上的正确率来提高推广能力, $\theta$ 在数值上越小越好,这样能抵抗数值的扰动。同时为了保证模型的正确率 $\theta$ 又不能极小。 故而人们将原来的损失函数加上一个惩罚项;

正则项

• L1正则项
  $$L_1=\sum _{i=1}^m\left|{\theta }_i\right|$$
• L2正则项
  $$L_2=\sum _{i=1}^m{\theta }_i^2$$

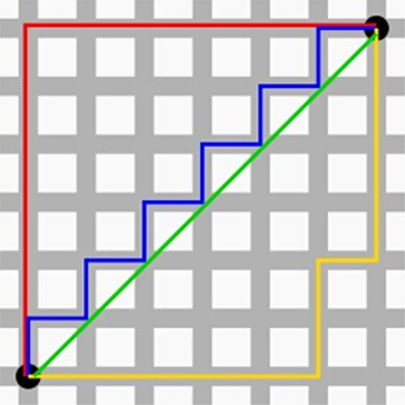
正则项其实就是范数, 代表代表空间中向量到原点的距离;并非所有距离都像我们几何中的距离, 只有欧氏空间的距离度量是用平方和开根来计算; L1范数就是曼哈顿距离, 如下图,绿色的就是欧式距离,其他都是曼哈都距离:

Lasso回归 和 Ridge岭回归

在原有的多元线性回归的Loss后加上一个L1正则项后,就产生Lasso回归

在原有的多元线性回归的Loss后加上一个L2正则项后,就产生Ridge岭回归

L1稀疏L2平滑

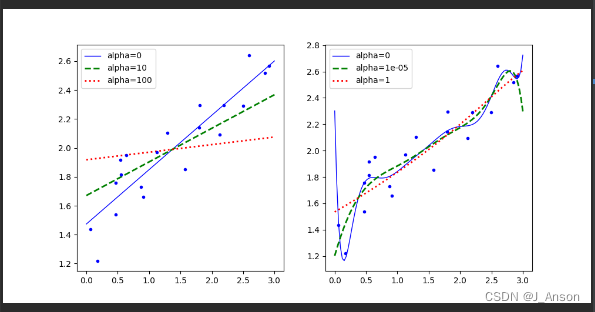
通常我们会说 L1 正则会使得计算出来的模型有的 $\theta$ 趋近于 0，有的 $\theta$ 相对较大，而 L2 会使得 $\theta$ 参数整体变小，这是为什么呢？

• 从梯度下降法考虑

  • Lasso回归

    Loss函数:
    $$Los{s}_{Lasso}=\sum _{i=1}^m(\hat{y}-y{)}^2+\lambda \sum _{i=1}^n\left|{\theta }_i\right|$$
    梯度:
    $$g_j^{Ridge}=({\theta }^{T}X-Y)x_j\pm \lambda$$

  • Ridge岭回归

    Loss函数:
    $$Los{s}_{Ridge}=\sum _{i=1}^m(\hat{y}-y{)}^2+\frac{\lambda }{2}\sum _{i=1}^n{\theta }_i^2$$
    梯度:
    $$g_j^{Ridge}=({\theta }^{T}X-Y)x_j+\lambda {\theta }_i$$

我们可以看到是 L1 每次会多走$\eta$的幅度,我们知道$\eta$学习率一开始设置一个常数,学习率是 0.5 的话,比如${\theta }_1$ 多走 0.5,${\theta }_2$ 也是多走 0.5,反观 L2 每次多走的幅度是之前的 2 倍的 ${\theta }_i^t$,学习率是 0.5 的话,那么就${\theta }_1$就多走${\theta }_1^t$,${\theta }_2$ 就多走 ${\theta }_2^t$;

观察上图, 红色区域其实是正则项本身的一个函数等高线图, 而紫色区域是原Loss的等高线图,要使他们的之和最小的$\theta$就是他们的交点处(细品, 把这两个函数当作三维图的话,他俩一叠加,最小值就出现在交点处)

而对于L1,交点常会出现在坐标轴上, 而L2会使得$\theta$都减小

• 深入理解L1稀疏L2平滑

接着上图, 对于原本Loss的最小点(紫色点), 加上正则项,他就得往原点附近靠;

而根据Lasso的导数, $\theta$的移动步长都一样(即${\theta }_1$向左走一单位, 那${\theta }_2$也会向下走一单位), 这样一走容易走到坐标轴上(如果提前与方形区域相交, 就不会在坐标轴上)

但对于Ridge岭回归来说, 当${\theta }_1$越接近0的时候,它走的就越慢, 就相当于在等待${\theta }_2$接近0, 所以L2与L2等高线相交的位置一般不会是坐标轴;

L1稀疏的应用–特征选择

因为L1稀疏, 有一些${\theta }_j$会变为0, 就意味着这些属性的数据其实是没啥意义的, 就可以帮助我们筛掉一些特征, 减少计算量, 让我们专注在重要特征的处理上;

Lasso与Ridge例子

• Ridge(L2)

#%%ridge_regression岭回归(l2)
import numpy as np
from sklearn.linear_model import Ridgenp.random.seed(2)
x = 2*np.random.rand(100,1)
#观察值         误差（服从正态分布）
y = 5 + 4*x + np.random.randn(100,1)reg = Ridge(alpha = 0.4,solver = 'sag')  #sag表示随机梯度下降
reg.fit(x,y)   #这里的x不用传截距项
print(reg.predict([[2]]))  #这里预测值一定要是矩阵形式（二维数组）
print(reg.intercept_)
print(reg.coef_)

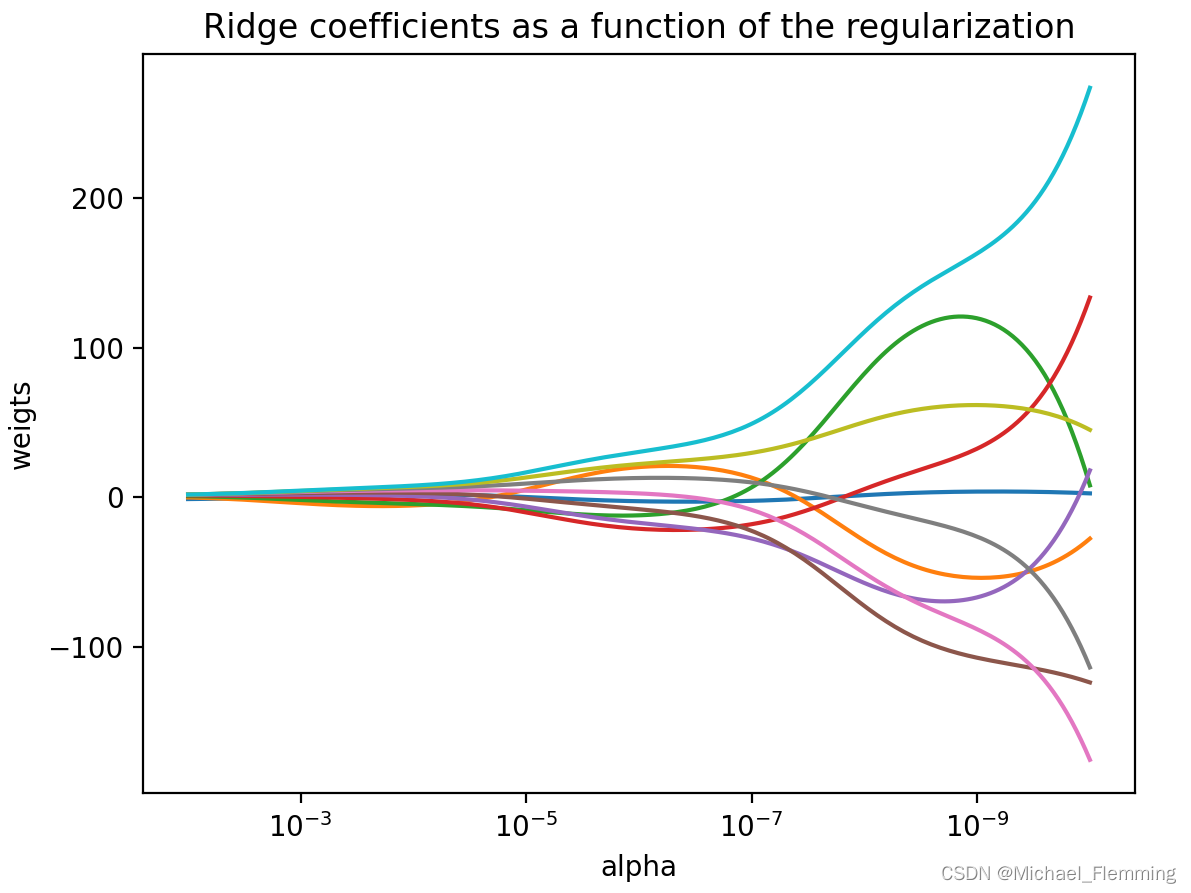
可以尝试修改一下alpha参数, alpha越大就表明越看重模型的泛化能力, 当alpha设置为0时, 就相当于普通的多元线性回归, 如果设置为0, 跑一把模型, 会显示Coordinate descent with no regularization may lead to unexpected results and is discouraged.其实就是说没设置正则项;

• Lasso(L1)

#%%lasso regression(L1正则项)
import numpy as np
from sklearn.linear_model import Lassonp.random.seed(2)
x = 2*np.random.rand(100,1)
#观察值         误差（服从正态分布）
y = 5 + 4*x + np.random.randn(100,1)reg = Lasso(alpha = 0.4,max_iter=1000000)  #这里无需传入梯度下降的方法 max_iter表示迭代次数
reg.fit(x,y)   #这里的x不用传截距项
print(reg.predict([[2]]))  #这里预测值一定要是矩阵形式（二维数组）
print(reg.intercept_)
print(reg.coef_)

L1和L2正则项同时作用 – ElasticNet

ElasticNet就是把Loss同时加上了L1正则和L2正则,没啥特别的
$$Los{s}_{ElasticNet}=\sum _{i=1}^m(\hat{y}-y{)}^2+\lambda \rho \sum _{i=1}^n\left|{\theta }_i\right|+\frac{\lambda (1-\rho )}{2}\sum _{i=1}^n{\theta }_i^2$$

ElasticNet例子

#%%ElasticNet （既使用L1，也使用L2）
import numpy as np
from sklearn.linear_model import ElasticNetnp.random.seed(2)
x = 2*np.random.rand(100,1)
#观察值         误差（服从正态分布）
y = 5 + 4*x + np.random.randn(100,1)reg = ElasticNet(alpha = 0.4,l1_ratio = 0.5,max_iter=1000000)  #这里无需传入梯度下降的方法 max_iter表示迭代次数
reg.fit(x,y)   #这里的x不用传截距项
print(reg.predict([[2]]))  #这里预测值一定要是矩阵形式（二维数组）
print(reg.intercept_)
print(reg.coef_)

多元线性回归的改进Ridge和Lasso就是这样了, 继续下一章吧！pd的Machine Learning