手写算法-python代码实现Ridge回归
- Ridge简介
- Ridge回归分析与python代码实现
- 方法一:梯度下降法求解Ridge回归参数
- 方法二:标准方程法实现Ridge回归
- 调用sklearn对比
Ridge简介
前面2篇文章,我们介绍了过拟合与正则化,比较全面的讲了L1、L2正则化的原理与特点;
链接: 原理解析-过拟合与正则化
以及python代码实现Lasso回归;
链接: 手写算法-python代码实现Lasso回归
今天,我们在这基础上,讲一讲Ridge回归,就比较简单了,
本文主要实现python代码的Ridge回归(带L2正则项),并用实例佐证原理。
Ridge回归分析与python代码实现
引用上篇文章的生成的数据集:
import numpy as np
from matplotlib import pyplot as plt
import sklearn.datasets#生成100个一元回归数据集
x,y = sklearn.datasets.make_regression(n_features=1,noise=5,random_state=2020)
plt.scatter(x,y)
plt.show()#加5个异常数据,为什么这么加,大家自己看一下生成的x,y的样子
a = np.linspace(1,2,5).reshape(-1,1)
b = np.array([350,380,410,430,480])#生成加入异常数据后新的数据集
x_1 = np.r_[x,a]
y_1 = np.r_[y,b]plt.scatter(x_1,y_1)
plt.show()


以上分别是正常数据集和加入了5个异常数据的图像,如果直接用线性回归拟合:
class normal():def __init__(self):passdef fit(self,x,y):m=x.shape[0]X = np.concatenate((np.ones((m,1)),x),axis=1)xMat=np.mat(X)yMat =np.mat(y.reshape(-1,1))xTx=xMat.T*xMat#xTx.I为xTx的逆矩阵ws=xTx.I*xMat.T*yMat#返回参数return wsplt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
clf1 =normal()
#拟合原始数据
w1 = clf1.fit(x,y)
#预测数据
y_pred = x * w1[1] + w1[0]#拟合新数据
w2 = clf1.fit(x_1,y_1)
#预测数据
y_1_pred = x_1 * w2[1] + w2[0]print('原始样本拟合参数:\n',w1)
print('\n')
print('新样本拟合参数:\n',w2)ax1= plt.subplot()
ax1.scatter(x_1,y_1,label='样本分布')
ax1.plot(x,y_pred,c='y',label='原始样本拟合')
ax1.plot(x_1,y_1_pred,c='r',label='新样本拟合')
ax1.legend(prop = {'size':15}) #此参数改变标签字号的大小
plt.show()

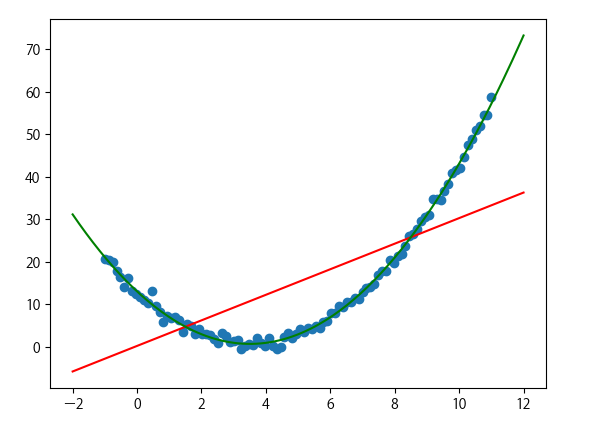
因为几个异常点数据,新的拟合回归线参数变大了很多,从19点多变成了47点多;脱离了实际数据的分布,模型性能下降。
我们加入L2正则项,来调优模型。下面是L2正则化的损失函数;
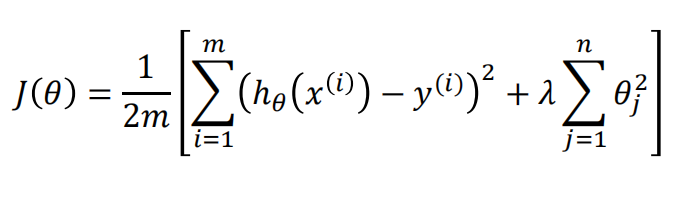
方法一:梯度下降法求解Ridge回归参数
前面文章我们都推导过线性回归的梯度和L2正则项的梯度,这个的梯度就是两者相加,算了,还是写一下:
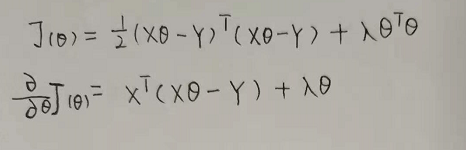
编写python代码如下(就是在原来的线性回归梯度上,加上L2的梯度):
class ridge():def __init__(self):pass#梯度下降法迭代训练模型参数,x为特征数据,y为标签数据,a为学习率,epochs为迭代次数,Lambda为正则项参数def fit(self,x,y,a,epochs,Lambda): #计算总数据量m=x.shape[0]#给x添加偏置项X = np.concatenate((np.ones((m,1)),x),axis=1)#计算总特征数n = X.shape[1]#初始化W的值,要变成矩阵形式W=np.mat(np.ones((n,1)))#X转为矩阵形式xMat = np.mat(X)#y转为矩阵形式,这步非常重要,且要是m x 1的维度格式yMat =np.mat(y.reshape(-1,1))#循环epochs次for i in range(epochs):gradient = xMat.T*(xMat*W-yMat)/m + Lambda * WW=W-a * gradientreturn Wdef predict(self,x,w): #这里的x也要加偏置,训练时x是什么维度的数据,预测也应该保持一样return np.dot(x,w)
ridge()函数来实现我们的Ridge回归,示例(以下的参数都是我经过调试,确认可以使模型收敛,继续加大迭代次数或者改变学习率,最终的模型系数也不改变):
当Lambda参数为0时,也就是不加L2正则项时,就是普通的线性回归,参数输出都是一样的,也是47点多
#Lambda=0时;
clf = ridge()
w = clf.fit(x_1,y_1,a = 0.001,epochs = 10000,Lambda=0)
print(w)#计算新的拟合值
y_1_pred = x_1 * w[1] + w[0]ax1= plt.subplot()
ax1.scatter(x_1,y_1,label='样本分布')
ax1.plot(x,y_pred,c='y',label='原始样本拟合')
ax1.plot(x_1,y_1_pred,c='r',label='新样本拟合')
ax1.legend(prop = {'size':15}) #此参数改变标签字号的大小
plt.show()

当Lambda =0.5时,参数变为31点多;
#Lambda=0.5时;
clf = ridge()
w = clf.fit(x_1,y_1,a = 0.001,epochs = 10000,Lambda=0.5)
print(w)#计算新的拟合值
y_1_pred = x_1 * w[1] + w[0]ax1= plt.subplot()
ax1.scatter(x_1,y_1,label='样本分布')
ax1.plot(x,y_pred,c='y',label='原始样本拟合')
ax1.plot(x_1,y_1_pred,c='r',label='新样本拟合')
ax1.legend(prop = {'size':15}) #此参数改变标签字号的大小
plt.show()

当Lambda =1.5时,参数变为18点多,基本上已经和没添加异常值的参数是一样的了;
#Lambda=1.5时;
clf = ridge()
w = clf.fit(x_1,y_1,a = 0.001,epochs = 10000,Lambda=1.5)
print(w)#计算新的拟合值
y_1_pred = x_1 * w[1] + w[0]ax1= plt.subplot()
ax1.scatter(x_1,y_1,label='样本分布')
ax1.plot(x,y_pred,c='y',label='原始样本拟合')
ax1.plot(x_1,y_1_pred,c='r',label='新样本拟合')
ax1.legend(prop = {'size':15}) #此参数改变标签字号的大小
plt.show()

当Lambda =20时,参数是2点多,拟合线差不多就是一条水平线了,此时严重欠拟合,损失函数值很大,模型完全没有收敛;
#Lambda=20时;
clf = ridge()
w = clf.fit(x_1,y_1,a = 0.001,epochs = 10000,Lambda=20)
print(w)#计算新的拟合值
y_1_pred = x_1 * w[1] + w[0]ax1= plt.subplot()
ax1.scatter(x_1,y_1,label='样本分布')
ax1.plot(x,y_pred,c='y',label='原始样本拟合')
ax1.plot(x_1,y_1_pred,c='r',label='新样本拟合')
ax1.legend(prop = {'size':15}) #此参数改变标签字号的大小
plt.show()

可以发现,合适的L2正则项参数,可以防止过拟合;
当Lambda参数一越来越大时,模型参数也越来越小,慢慢接近于0。
方法二:标准方程法实现Ridge回归
接下来,我们用标准方程法实现Ridge回归,推导公式如下:
 python代码实现如下:
python代码实现如下:
class standard_ridge():def __init__(self):passdef fit(self,x,y,Lambda):m = x.shape[0]X = np.concatenate((np.ones((m,1)),x),axis=1)xMat= np.mat(X)yMat = np.mat(y.reshape(-1,1))xTx = xMat.T * xMat#生成单位矩阵,2个矩阵行列相等才可以相加#前面的梯度下降法代码中,我们没有省掉m,因此,我们化简时,也不省掉m,最后形式就是在正则项梯度这里乘以m,其实不会造成本质影响rxTx = xTx + np.eye(xMat.shape[1]) * Lambda * m#rxTx.I为rxTx的逆矩阵w = rxTx.I * xMat.T * yMatreturn w
以下是运行结果:

基本上结果一样,但是这种形式,更简洁方便一些。
调用sklearn对比
from sklearn.linear_model import Ridge
lr=Ridge(alpha=0)
lr.fit(x_1,y_1)
print('alpha=0时',lr.coef_,'\n')lr=Ridge(alpha=40)
lr.fit(x_1,y_1)
print('alpha=40时',lr.coef_,'\n')lr=Ridge(alpha=150)
lr.fit(x_1,y_1)
print('alpha=150时',lr.coef_,'\n')lr=Ridge(alpha=2000)
lr.fit(x_1,y_1)
print('alpha=2000时',lr.coef_)

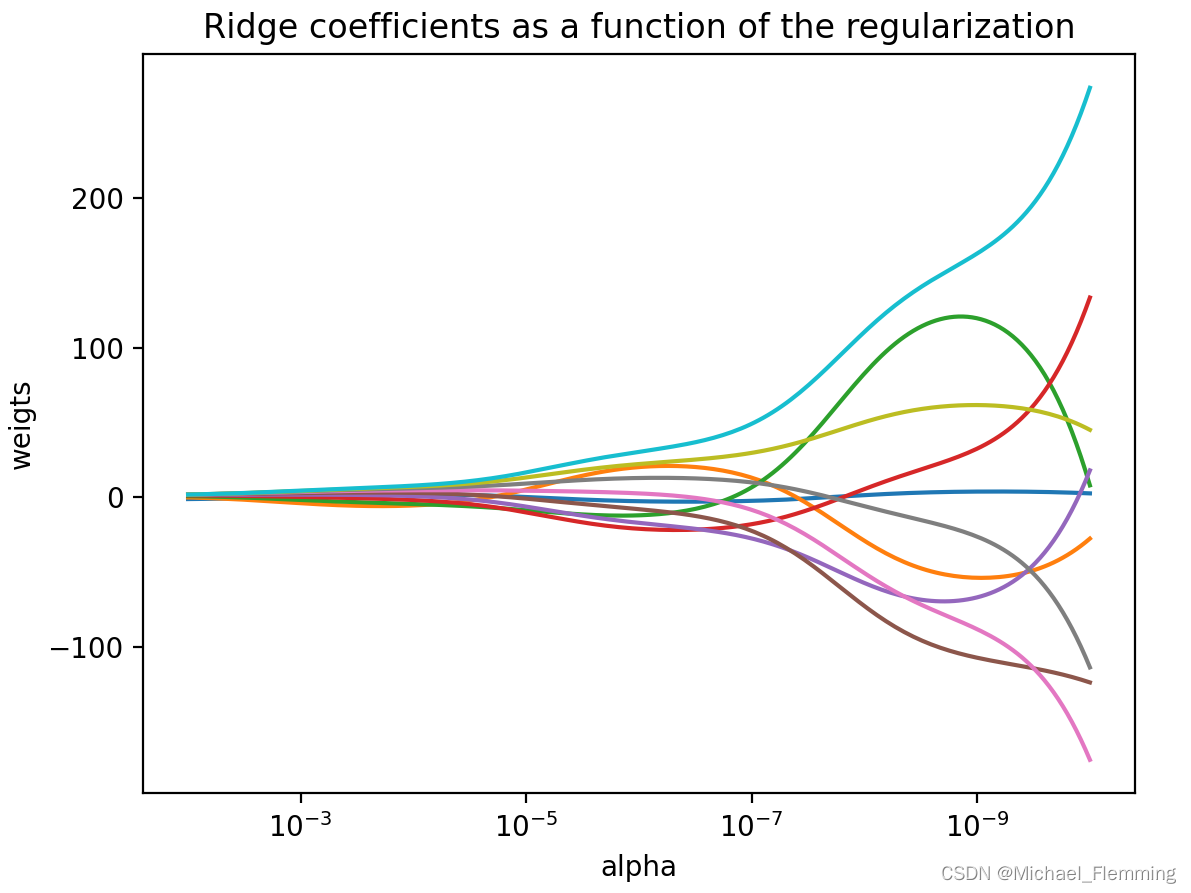
sklearn展示Ridge:
1、随着alpha值的增大,也就是正则项系数增大,系数变得越来越接近于0,但是没有等于0的。
#用波士顿房价回归数据集展示
data = sklearn.datasets.load_boston()
x =data['data']
y= data['target']lr=Ridge(alpha=0)
lr.fit(x,y)
print('alpha=0时',lr.coef_,'\n')lr=Ridge(alpha=10)
lr.fit(x,y)
print('alpha=10时',lr.coef_,'\n')lr=Ridge(alpha=100)
lr.fit(x,y)
print('alpha=100时',lr.coef_,'\n')lr=Ridge(alpha=1000)
lr.fit(x,y)
print('alpha=1000时',lr.coef_)

总结:线性回归系列我们就介绍到这里了,因为很多概念都是第一次讲,所以写的很细致,辅以数据实例展示,保证读者可以看得懂,同时手动复现,这些基础概念讲清楚了,也方便后面讲解复杂算法。
接下来介绍逻辑回归。










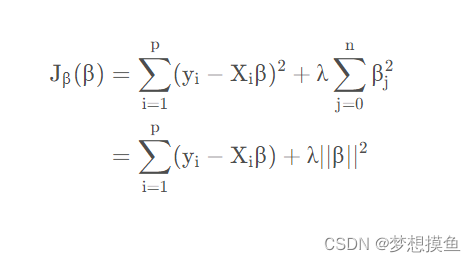


![[组原]初识-地址总线,地址寄存器,存储单元,存储字长](https://img-blog.csdnimg.cn/fec3f6f79ccb4139a78eac6fde3ece22.png)

