阅读本文需要的背景知识点:标准线性回归算法、一丢丢编程知识
一、引言
前面一节我们学习了机器学习算法系列(三)- 标准线性回归算法(Standard Linear Regression Algorithm),最后求得标准线性回归的代价函数的解析解 w 为:
w = ( X T X ) − 1 X T y w=\left(X^{T} X\right)^{-1} X^{T} y w=(XTX)−1XTy
其中提到如果矩阵 X 的转置与矩阵 X 相乘后的矩阵不是满秩矩阵时,这个矩阵是不可逆的,还提到其本质是多个自变量 x 之间存在多重共线性。下面来介绍多重共线性的问题与解决这个问题的其中一个方法 - 岭回归1(Ridge Regression)
二、多重共线性
先来看看多重共线性在维基百科中的解释:
多重共线性2(Multicollinearity)是指多变量线性回归中,变量之间由于存在精确相关关系或高度相关关系而使回归估计不准确。
那么什么是精确相关关系与高度相关关系呢?假如有下面的(1)式,其中 w 1 = 2 、 w 2 = 3 w_1 = 2、w_2 = 3 w1=2、w2=3,同时如果又存在(2)式的关系,这时就说明 x 1 x_1 x1 与 x 2 x_2 x2 存在精确相关关系。当 x 1 x_1 x1 与 x 2 x_2 x2 之间存在近似精确相关关系,例如 x 1 x_1 x1 约等于 2 倍的 x 2 x_2 x2,则说明存在高度相关关系。
{ y = 2 x 1 + 3 x 2 ( 1 ) x 2 = 2 x 1 ( 2 ) \left\{\begin{array}{l} y=2 x_{1}+3 x_{2} & (1)\\ x_{2}=2 x_{1} & (2) \end{array}\right. {y=2x1+3x2x2=2x1(1)(2)
因为由(2)式可以将(1)式改写成不同的形式,这样就会导致 w 存在无数种解,会使得最后的回归估计不准确。
⟹ { y = 2 x 1 + 3 x 2 ⇒ w 1 = 2 w 2 = 3 y = 8 x 1 ⇒ w 1 = 8 w 2 = 0 y = 4 x 2 ⇒ w 1 = 0 w 2 = 4 y = 6 x 1 + x 2 ⇒ w 1 = 6 w 2 = 1 … \Longrightarrow\left\{\begin{array}{lll} y=2 x_{1}+3 x_{2} & \Rightarrow w_{1}=2 & w_{2}=3 \\ y=8 x_{1} & \Rightarrow w_{1}=8 & w_{2}=0 \\ y=4 x_{2} & \Rightarrow w_{1}=0 & w_{2}=4 \\ y=6 x_{1}+x_{2} & \Rightarrow w_{1}=6 & w_{2}=1 \\ \ldots & & \end{array}\right. ⟹⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧y=2x1+3x2y=8x1y=4x2y=6x1+x2…⇒w1=2⇒w1=8⇒w1=0⇒w1=6w2=3w2=0w2=4w2=1
根据 w 的解析解,可以通过下面的公式来求解其中的逆矩阵运算,被除数为矩阵的伴随矩阵3,除数为矩阵的行列式。可以看到矩阵可逆的条件是其行列式不能为零。
( X T X ) − 1 = ( X T X ) ∗ ∣ X T X ∣ \left(X^TX\right)^{-1} = \frac{\left(X^TX\right)^*}{\mid X^TX \mid } (XTX)−1=∣XTX∣(XTX)∗
如果自变量之间存在多重共线性,会使得矩阵的行列式为零,导致矩阵不可逆。如下图中的示例 X,可以看到 x 1 x_1 x1 与 x 2 x_2 x2 存在精确相关关系,相乘后的矩阵经过初等变换4后其行列式为零,说明相乘后的矩阵的行列式也必然为零(初等变换不改变行列式为零的判断),这时的矩阵不可逆。如果自变量之间是高度相关关系,会使得矩阵的行列式近似等于零,这时所得的 w 的偏差会很大,也会造成回归估计不准确。
X = [ 1 1 2 1 2 4 1 3 6 1 4 8 ] X T = [ 1 1 1 1 1 2 3 4 2 4 6 8 ] X T X = [ 4 10 20 10 30 60 20 60 120 ] ⟶ 初等变换 [ 1 0 0 0 1 2 0 0 0 ] \begin{array}{c} X=\left[\begin{array}{lll} 1 & 1 & 2 \\ 1 & 2 & 4 \\ 1 & 3 & 6 \\ 1 & 4 & 8 \end{array}\right] \quad X^{T}=\left[\begin{array}{llll} 1 & 1 & 1 & 1 \\ 1 & 2 & 3 & 4 \\ 2 & 4 & 6 & 8 \end{array}\right] \\ X^{T} X=\left[\begin{array}{ccc} 4 & 10 & 20 \\ 10 & 30 & 60 \\ 20 & 60 & 120 \end{array}\right] \stackrel{\text { 初等变换 }}{\longrightarrow}\left[\begin{array}{lll} 1 & 0 & 0 \\ 0 & 1 & 2 \\ 0 & 0 & 0 \end{array}\right] \end{array} X=⎣⎢⎢⎡111112342468⎦⎥⎥⎤XT=⎣⎡112124136148⎦⎤XTX=⎣⎡410201030602060120⎦⎤⟶ 初等变换 ⎣⎡100010020⎦⎤
多重共线性的问题既然是自变量之间存在相关关系,其中一个解决方法就是剔除掉共线的自变量,可以通过计算方差扩大因子5(Variance inflation factor,VIF)来量化自变量之间的相关关系,方差扩大因子越大说明自变量的共线性越严重。
另一种方式是通过对代价函数正则化加入惩罚项来解决,其中一种正则化方式被称为吉洪诺夫正则化(Tikhonov regularization),这种代价函数正则化后的线性回归被称为岭回归(Ridge Regression)。
三、算法步骤
岭回归的代价函数第一项与标准线性回归的一致,都是欧几里得距离的平方和,只是在后面加上了一个 w 向量的 L2-范数6 的平方作为惩罚项(L2-范数的含义为向量 W 每个元素的平方和然后开平方),其中 λ 表示惩罚项的系数,人为的控制惩罚项的大小。由于正则项是 L2-范数,有时这种正则化方式也被称为 L2 正则化。
Cost ( w ) = ∑ i = 1 N ( y i − w T x i ) 2 + λ ∥ w ∥ 2 2 \operatorname{Cost}(w) = \sum_{i = 1}^N \left( y_i - w^Tx_i \right)^2 + \lambda\|w\|_{2}^{2} Cost(w)=i=1∑N(yi−wTxi)2+λ∥w∥22
同标准线性回归一样,也是求使得岭回归的代价函数最小时 w 的大小:
w = argmin w ( ∑ i = 1 N ( y i − w T x i ) 2 + λ ∥ w ∥ 2 2 ) w=\underset{w}{\operatorname{argmin}}\left(\sum_{i=1}^{N}\left(y_{i}-w^{T} x_{i}\right)^{2}+\lambda\|w\|_{2}^{2}\right) w=wargmin(i=1∑N(yi−wTxi)2+λ∥w∥22)
代价函数通过求导直接得到 w 的解析解,其中 X 为 N x M 矩阵,y 为 N 维列向量, λ 属于实数集,I 为 M x M 的单位矩阵。
w = ( X T X + λ I ) − 1 X T y λ ∈ R w=\left(X^{T} X+\lambda I\right)^{-1} X^{T}y \quad \lambda \in \mathbb{R} w=(XTX+λI)−1XTyλ∈R
X = [ x 1 T x 2 T ⋮ x N T ] = [ X 11 X 12 ⋯ X 1 M X 21 X 22 ⋯ X 2 M ⋮ ⋮ ⋱ ⋮ X N 1 X N 2 ⋯ X N M ] y = ( y 1 y 2 ⋮ y N ) X=\left[\begin{array}{c} x_{1}^{T} \\ x_{2}^{T} \\ \vdots \\ x_{N}^{T} \end{array}\right]=\left[\begin{array}{cccc} X_{11} & X_{12} & \cdots & X_{1 M} \\ X_{21} & X_{22} & \cdots & X_{2 M} \\ \vdots & \vdots & \ddots & \vdots \\ X_{N 1} & X_{N 2} & \cdots & X_{N M} \end{array}\right] \quad y=\left(\begin{array}{c} y_{1} \\ y_{2} \\ \vdots \\ y_{N} \end{array}\right) X=⎣⎢⎢⎢⎡x1Tx2T⋮xNT⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡X11X21⋮XN1X12X22⋮XN2⋯⋯⋱⋯X1MX2M⋮XNM⎦⎥⎥⎥⎤y=⎝⎜⎜⎜⎛y1y2⋮yN⎠⎟⎟⎟⎞
四、原理证明
岭回归代价函数为凸函数
同样需要证明:
f ( x 1 + x 2 2 ) ≤ f ( x 1 ) + f ( x 2 ) 2 f\left(\frac{x_{1}+x_{2}}{2}\right) \leq \frac{f\left(x_{1}\right)+f\left(x_{2}\right)}{2} f(2x1+x2)≤2f(x1)+f(x2)
不等式左边:
Cost ( w 1 + w 2 2 ) = ∑ i = 1 N [ ( w 1 + w 2 2 ) T x i − y i ] 2 + λ ∥ w 1 + w 2 2 ∥ 2 2 \operatorname{Cost}\left(\frac{w_{1}+w_{2}}{2}\right)=\sum_{i=1}^{N}\left[\left(\frac{w_{1}+w_{2}}{2}\right)^{T} x_{i}-y_{i}\right]^{2}+\lambda\left\|\frac{w_{1}+w_{2}}{2}\right\|_{2}^{2} Cost(2w1+w2)=i=1∑N[(2w1+w2)Txi−yi]2+λ∥∥∥∥2w1+w2∥∥∥∥22
不等式右边:
Cost ( w 1 ) + Cost ( w 2 ) 2 = ∑ i = 1 N ( w 1 T x i − y i ) 2 + ∑ i = 1 N ( w 2 T x i − y i ) 2 + λ ∥ w 1 ∥ 2 2 + λ ∥ w 2 ∥ 2 2 2 \frac{\operatorname{Cost}\left(w_{1}\right)+\operatorname{Cost}\left(w_{2}\right)}{2}=\frac{\sum_{i=1}^{N}\left(w_{1}^{T} x_{i}-y_{i}\right)^{2}+\sum_{i=1}^{N}\left(w_{2}^{T} x_{i}-y_{i}\right)^{2}+\lambda\left\|w_{1}\right\|_{2}^{2}+\lambda\left\|w_{2}\right\|_{2}^{2}}{2} 2Cost(w1)+Cost(w2)=2∑i=1N(w1Txi−yi)2+∑i=1N(w2Txi−yi)2+λ∥w1∥22+λ∥w2∥22
(1)不等式两边的前半部分与标准线性回归一致,只需要证明剩下的差值大于等于零即可
(2)将其改写成向量点积的形式
(3)展开括号
(4)合并相同的项, w 1 w_1 w1 的转置乘 w 2 w_2 w2 与 w 2 w_2 w2 的转置乘 w 1 w_1 w1 互为转置,又因为结果为实数,所以这个两项可以合并
(5)可以写成向量的平方的形式
Δ = λ ∥ w 1 ∥ 2 2 + λ ∥ w 2 ∥ 2 2 − 2 λ ∥ w 1 + w 2 2 ∥ 2 2 ( 1 ) = λ [ w 1 T w 1 + w 2 T w 2 − 2 ( w 1 + w 2 2 ) T ( w 1 + w 2 2 ) ] ( 2 ) = λ ( w 1 T w 1 + w 2 T w 2 − w 1 T w 1 + w 2 T w 2 + w 1 T w 2 + w 2 T w 1 2 ) ( 3 ) = λ 2 ( w 1 T w 1 + w 2 T w 2 − 2 w 1 T w 2 ) ( 4 ) = λ 2 ( w 1 − w 2 ) T ( w 1 − w 2 ) ( 5 ) \begin{aligned} \Delta &=\lambda\left\|w_{1}\right\|_{2}^{2}+\lambda\left\|w_{2}\right\|_{2}^{2}-2 \lambda\left\|\frac{w_{1}+w_{2}}{2}\right\|_{2}^{2} & (1) \\ &=\lambda\left[w_{1}^{T} w_{1}+w_{2}^{T} w_{2}-2\left(\frac{w_{1}+w_{2}}{2}\right)^{T}\left(\frac{w_{1}+w_{2}}{2}\right)\right] & (2) \\ &=\lambda\left(w_{1}^{T} w_{1}+w_{2}^{T} w_{2}-\frac{w_{1}^{T} w_{1}+w_{2}^{T} w_{2}+w_{1}^{T} w_{2}+w_{2}^{T} w_{1}}{2}\right) & (3) \\ &=\frac{\lambda}{2}\left(w_{1}^{T} w_{1}+w_{2}^{T} w_{2}-2 w_{1}^{T} w_{2}\right) & (4) \\ &=\frac{\lambda}{2}\left(w_{1}-w_{2}\right)^{T}\left(w_{1}-w_{2}\right) & (5) \end{aligned} Δ=λ∥w1∥22+λ∥w2∥22−2λ∥∥∥∥2w1+w2∥∥∥∥22=λ[w1Tw1+w2Tw2−2(2w1+w2)T(2w1+w2)]=λ(w1Tw1+w2Tw2−2w1Tw1+w2Tw2+w1Tw2+w2Tw1)=2λ(w1Tw1+w2Tw2−2w1Tw2)=2λ(w1−w2)T(w1−w2)(1)(2)(3)(4)(5)
不等式右边减去不等式左边的差值为平方式的连加运算加上两向量差的平方,人为的控制 λ 的大小,最后的结果在实数范围内必然大于等于零,证毕。
岭回归代价函数的解析解
(1)岭回归的代价函数
(2)前面三项为标准线性回归代价函数展开后的结果,w 的 L2-范数的平方可以写成向量 w 的点积
(3)合并第一项与第四项
Cost ( w ) = ∑ i = 1 N ( y i − w T x i ) 2 + λ ∥ w ∥ 2 2 ( 1 ) = w T X T X w − 2 w T X T y + y T y + λ w T w ( 2 ) = w T ( X T X + λ I ) w − 2 w T X T y + y T y ( 3 ) \begin{aligned} \operatorname{Cost}(w) &=\sum_{i=1}^{N}\left(y_{i}-w^{T} x_{i}\right)^{2}+\lambda\|w\|_{2}^{2} & (1)\\ &=w^{T} X^{T} X w-2 w^{T} X^{T} y+y^{T} y+\lambda w^{T} w & (2)\\ &=w^{T}\left(X^{T} X+\lambda I\right) w-2 w^{T} X^{T} y+y^{T} y & (3) \end{aligned} Cost(w)=i=1∑N(yi−wTxi)2+λ∥w∥22=wTXTXw−2wTXTy+yTy+λwTw=wT(XTX+λI)w−2wTXTy+yTy(1)(2)(3)
(1)代价函数对 w 求偏导数,根据向量求导公式,只有第一项和第二项与 w 有关,最后一项为常数,又因为代价函数是个凸函数,当对 w 的偏导数为 0 向量时,代价函数为最小值。
(2)将第二项移项后同时除以 2,再两边同时在前面乘以一个逆矩阵,等式左边的矩阵和逆矩阵乘后为单位矩阵,所以只剩下 w 向量。
∂ Cost(w) ∂ w = 2 ( X T X + λ I ) w − 2 X T y = 0 ( 1 ) w = ( X T X + λ I ) − 1 X T y ( 2 ) \begin{aligned} \frac{\partial \operatorname{Cost(w)}}{\partial w} &= 2(X^TX + \lambda I)w - 2X^Ty = 0 & (1) \\ w &= (X^TX + \lambda I)^{-1}X^Ty & (2) \end{aligned} ∂w∂Cost(w)w=2(XTX+λI)w−2XTy=0=(XTX+λI)−1XTy(1)(2)
可以看到岭回归代价函数的解析解相较于标准线性回归来说多了一个可以人为控制的对角矩阵,这时可以通过调整不同的 λ 来使得括号内的矩阵可逆。
在上一节的工作年限与平均月工资的例子中,X 为 一个 5 x 2 的矩阵,y 为一个 5 维列向量,当 λ 为 0.1 时,最后可以算得 w 为一个 2 维列向量,则这个例子的线性方程为 y = 2139 ∗ x − 403.9 y = 2139 * x - 403.9 y=2139∗x−403.9。
X = [ 1 1 1 2 1 3 1 4 1 5 ] y = ( 1598 3898 6220 7799 10510 ) X = \begin{bmatrix} 1 & 1\\ 1 & 2\\ 1 & 3\\ 1 & 4\\ 1 & 5 \end{bmatrix} \quad y = \begin{pmatrix} 1598\\ 3898\\ 6220\\ 7799\\ 10510 \end{pmatrix} X=⎣⎢⎢⎢⎢⎡1111112345⎦⎥⎥⎥⎥⎤y=⎝⎜⎜⎜⎜⎛159838986220779910510⎠⎟⎟⎟⎟⎞
w = ( X T X + λ I ) − 1 X T y = ( − 403.9 2139.0 ) w = \left(X^TX + \lambda I\right)^{-1}X^Ty = \begin{pmatrix} -403.9\\ 2139.0 \end{pmatrix} w=(XTX+λI)−1XTy=(−403.92139.0)
可以看到加了惩罚项后,相较于标准线性回归的结果,拟合变差了,但是通过人为的控制惩罚项的大小,解决了自变量多重共线性的问题。
五、代码实现
使用 Python 实现线性回归算法:
import numpy as npdef ridge(X, y, lambdas=0.1):"""岭回归args:X - 训练数据集y - 目标标签值lambdas - 惩罚项系数return:w - 权重系数"""return np.linalg.inv(X.T.dot(X) + lambdas * np.eye(X.shape[1])).dot(X.T).dot(y)
六、第三方库实现
scikit-learn7 实现:
from sklearn.linear_model import Ridge# 初始化岭回归器
reg = Ridge(alpha=0.1, fit_intercept=False)
# 拟合线性模型
reg.fit(X, y)
# 权重系数
w = reg.coef_
七、示例演示
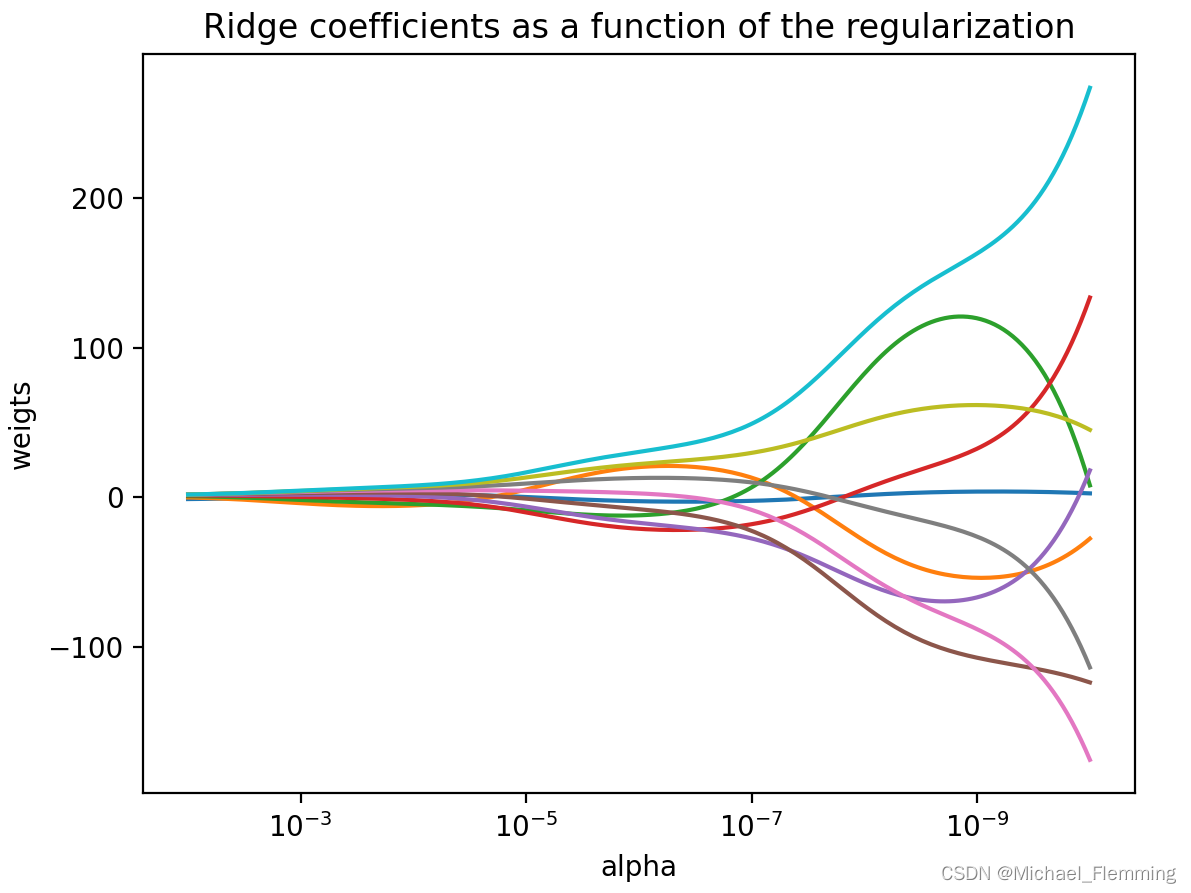
下图展示了惩罚系数 λ 对各个自变量的权重系数的影响,横轴为惩罚系数 λ ,纵轴为权重系数,每一个颜色表示一个自变量的权重系数:
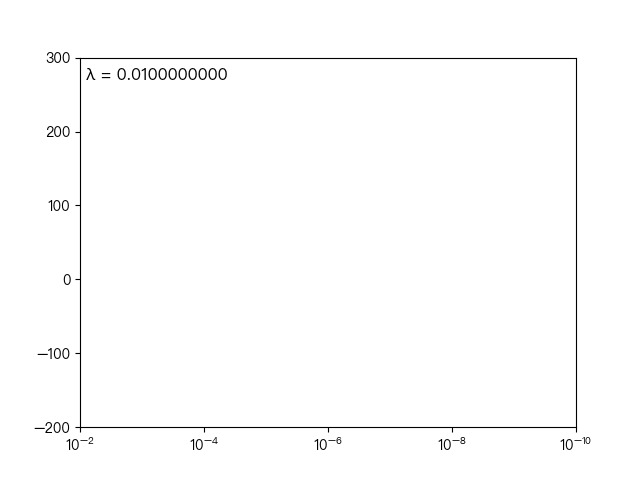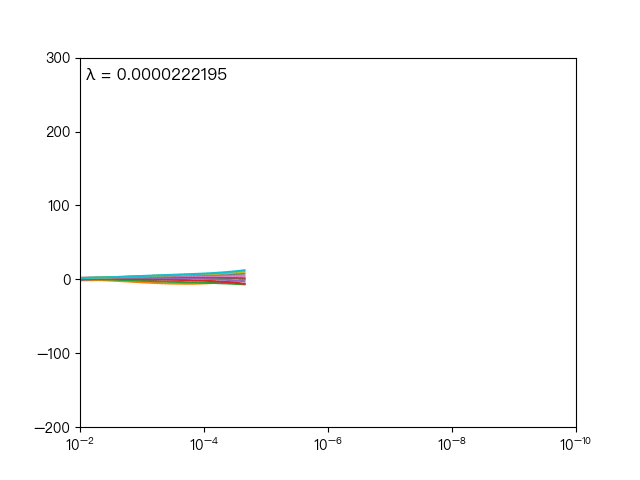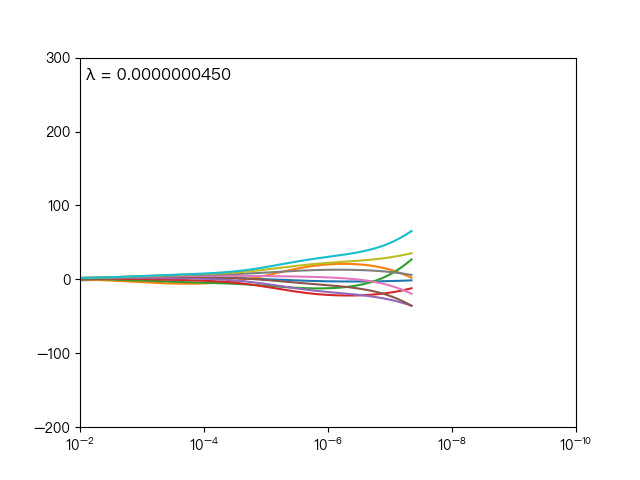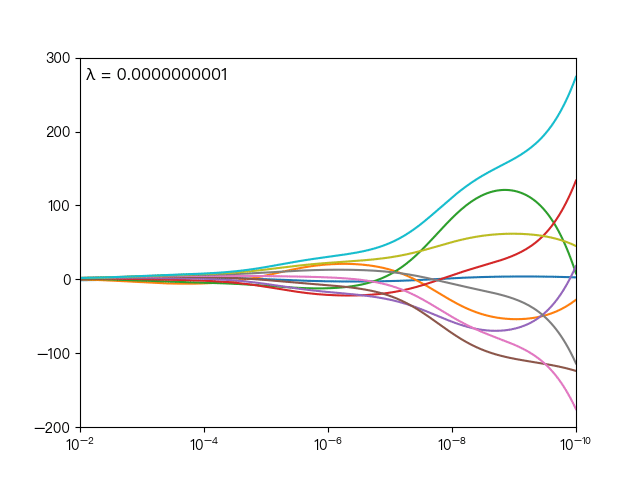
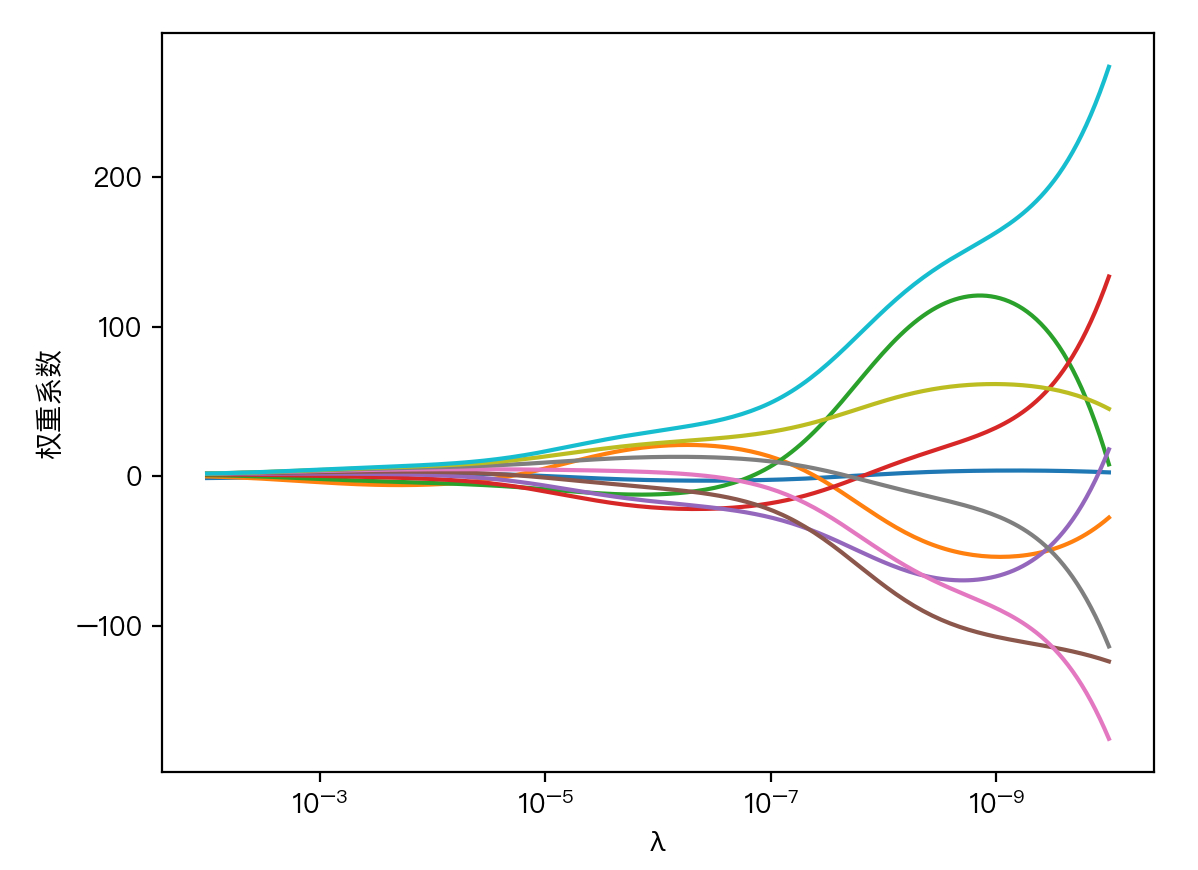
可以看到当 λ 越大时( λ 向左移动),惩罚项占据主导地位,会使得每个自变量的权重系数趋近于零,而当 λ 越小时( λ 向右移动),惩罚项的影响越来越小,会导致每个自变量的权重系数震荡的幅度变大。在实际应用中需要多次调整不同的 λ 值来找到一个合适的模型使得最后的效果最好。
八、思维导图
九、参考文献
- https://en.wikipedia.org/wiki/Tikhonov_regularization
- https://en.wikipedia.org/wiki/Multicollinearity
- https://en.wikipedia.org/wiki/Adjugate_matrix
- https://en.wikipedia.org/wiki/Elementary_matrix
- https://en.wikipedia.org/wiki/Variance_inflation_factor
- https://en.wikipedia.org/wiki/Norm_(mathematics)
- https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Ridge.html
完整演示请点击这里
注:本文力求准确并通俗易懂,但由于笔者也是初学者,水平有限,如文中存在错误或遗漏之处,恳请读者通过留言的方式批评指正
本文首发于——AI导图,欢迎关注











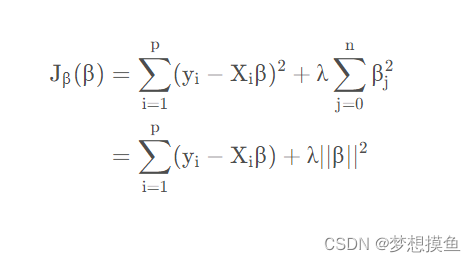


![[组原]初识-地址总线,地址寄存器,存储单元,存储字长](https://img-blog.csdnimg.cn/fec3f6f79ccb4139a78eac6fde3ece22.png)
