目录
- 1 基本库导入
- 2 线性回归
- 2.1 线性模型性能
- 2.2 使用更高维的数据集
- 3 岭回归-Ridge
- 3.1 Ridge原理及应用
- 3.2 Ridge调参
- 3.3 为什么要用Ridge
- 4 Lasso
- 4.1 基本原理及应用
- 4.2 Lasso调参
- 4.3 为什么要用Lasso
- 4.4 Lasso和Ridge的区别(L1,L2区别)
- 5 相关概念
- 5.1 模型偏差-模型方差
- 5.2 多重共线性相关
- 5.2.1 概念
- 5.2.2 影响
- 5.5.3 排除方法
1 基本库导入
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import mglearn
对于回归问题,线性模型预测的一般公式如下:
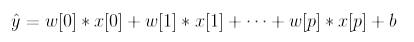
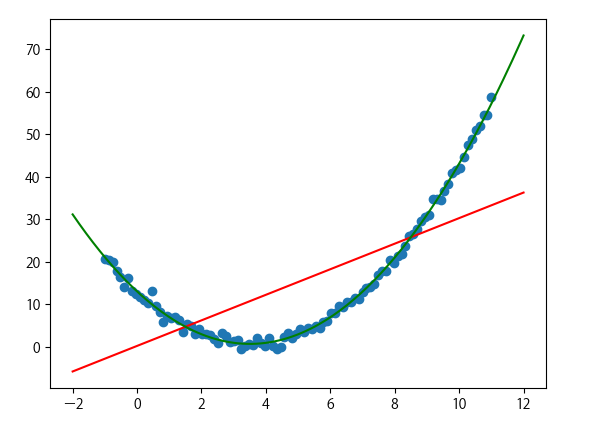
下列代码可以在一维 wave 数据集上学习参数 w [0] 和 b :
mglearn.plots.plot_linear_regression_wave()
2 线性回归
线性回归,或者普通最小二乘法 (ordinary least squares,OLS), 是回归问题最简单也最经典的线性方法。线性回归寻找参数 w 和 b ,使得对训练集的预测值与真实的回归目标值 y 之间的均方误差最小。均方误差(mean squared error)是预测值与真实值之差的平方和除以样本数。线性回归没有参数,这是一个优点,但也因此无法控制模型的复杂度。
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split# 数据集划分
X, y = mglearn.datasets.make_wave(n_samples = 60)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state = 1)# 训练模型
lr = LinearRegression().fit(X_train, y_train)
“斜率”参数(w,也叫作权重或系数 )被保存在 coef_ 属性中,而偏移或截距(b )被保存在 intercept_ 属性中。(coef_ 和 intercept_ 结尾处奇怪的下 划线。scikit-learn总是将从训练数据中得出的值保存在以下划线结尾的属性中。这是为了将其与用户设置的参数区分开)
lr.coef_
[out]: array([0.42056163])
lr.intercept_
[out]: -0.043819629242883185
2.1 线性模型性能
# 这个地方输出的是R^2
lr.score(X_train, y_train)
[out]: 0.6785798741099218
lr.score(X_test, y_test)
[out]: 0.623410671552743
R2 约为 0.66,这个结果不是很好,但我们可以看到,训练集和测试集上的分数非常接近。这说明可能存在欠拟合,而不是过拟合。 对于这个一维数据集来说,过拟合的风险很小,因为模型非常简单 (或受限)。然而,对于更高维的数据集(即有大量特征的数据集),线性模型将变得更加强大,过拟合的可能性也会变大。
2.2 使用更高维的数据集
X, y = mglearn.datasets.load_extended_boston()
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state = 1)lr = LinearRegression().fit(X_train, y_train)
lr.score(X_train, y_train)
[out]: 0.9281262443260945
lr.score(X_test, y_test)
[out]: 0.8962092351509625
若性能差异过大,则说明存在过拟合;若结果差异不大,但是性能不佳,则可能是欠拟合。
3 岭回归-Ridge
3.1 Ridge原理及应用
岭回归也是一种用于回归的线性模型,因此它的预测公式与普通最小二乘法相同。但在岭回归中,对系数(w)的选择不仅要在训练数据上得到好的预测结果,而且还要拟合附加约束。**我们还希望系数尽量小。换句话说,w 的所有元素都应接近于 0。**直观上来看, 这意味着每个特征对输出的影响应尽可能小(即斜率很小),同时仍给出很好的预测结果。这种约束是所谓正则化(regularization)的一个例子。正则化是指对模型做显式约束,以避免过拟合。岭回归用到的这种被称为 L2 正则化。
通常岭回归方程的R平方值会稍低于普通回归分析,但回归系数的显著性往往明显高于普通回归,在存在共线性问题和病态数据偏多的研究中有较大的实用价值。
from sklearn.linear_model import Ridgeridge = Ridge().fit(X_train, y_train)
print(f'Train set score: {ridge.score(X_train, y_train)}')
print(f'Test set score: {ridge.score(X_test, y_test)}')
print(f'The number of feature: {np.sum(ridge.coef_ != 0)}')
[out]:
Train set score: 0.8406599011793962
Test set score: 0.8836280810371685
The number of feature: 10
Ridge 是一种约束更强的模型,所以更不容易过拟合。复杂度更小的模型意味着在训练集上的性能更差,但泛化性能更好。
3.2 Ridge调参
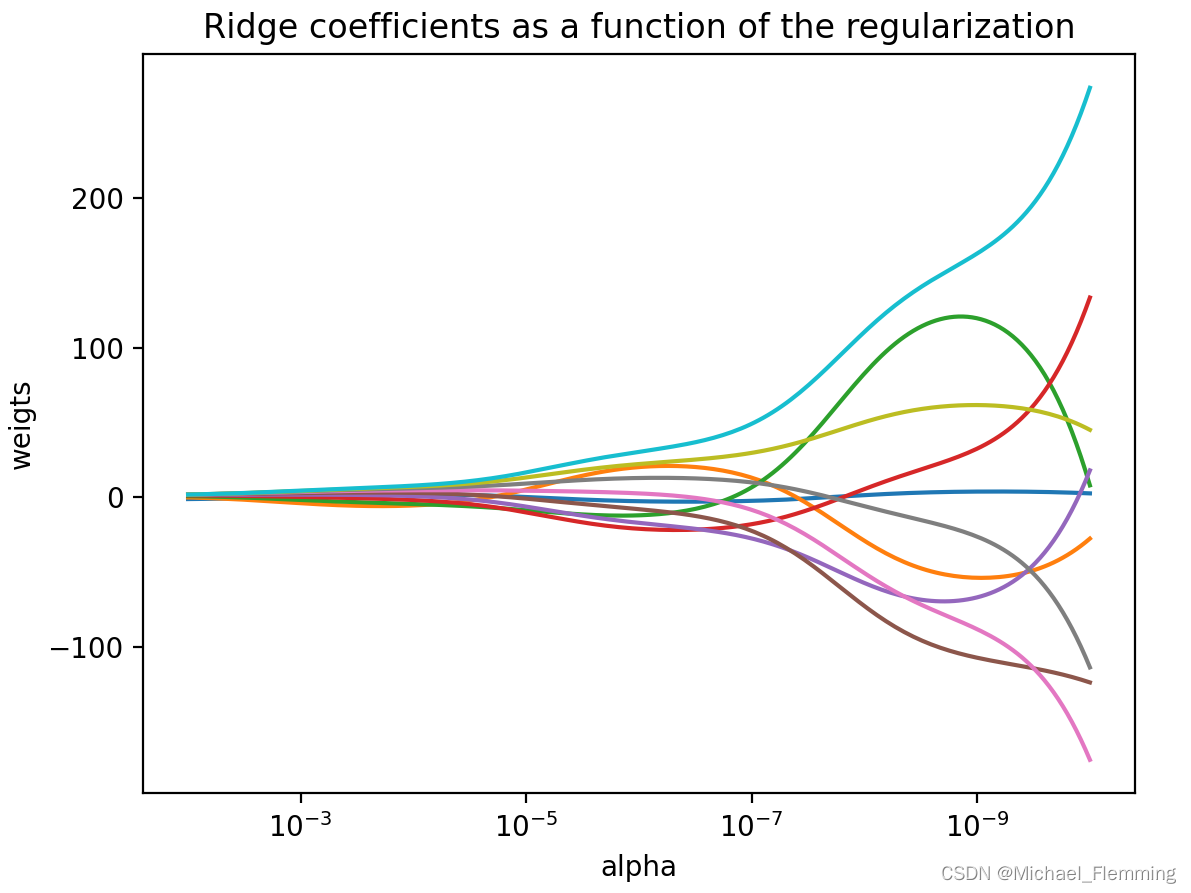
Ridge 模型在模型的简单性(系数都接近于 0)与训练集性能之间做出权衡。简单性和训练集性能二者对于模型的重要程度可以由用户通过设置 alpha参数来指定。在前面的例子中,我们用的是默认参数 alpha=1.0。但没有理由认为这会给出最佳权衡。alpha的最佳设定值取决于用到的具体数据集。增大alpha会使得系数更加趋向于0,从而降低训练集性能,但可能会提高泛化性能。
ridge10 = Ridge(alpha = 10).fit(X_train, y_train)
ridge01 = Ridge(alpha = 0.1).fit(X_train, y_train)
plt.plot(ridge.coef_, 's', label = 'Ridge alpha=1')
plt.plot(ridge10.coef_, 's', label = 'Ridge alpha=10')
plt.plot(ridge01.coef_, 's', label = 'Ridge alpha=0.1')plt.plot(lr.coef_, 'o', label = 'LinearRegression')
plt.xlabel('Coefficient index')
plt.ylabel('Coefficient magnitude')
plt.hlines(0, 0, len(lr.coef_))
plt.ylim(-25, 25)
plt.legend()
plt.show()

mglearn.plots.plot_ridge_n_samples()

如果有足够多的训练数据,正则化变得不那么重要,并且岭回归和线性回归将具有相同的性能。(在这个例子中,二者相同恰好 发生在整个数据集的情况下,这只是一个巧合)
3.3 为什么要用Ridge
总的来说,Ridge是使用是为了减少共线性的影响。
标准线性或多项式回归在特征变量之间存在很高的共线性(high collinearity)的情况下将失败。
我们进行回归分析需要了解每个自变量对因变量的单纯效应,高共线性就是说自变量间存在某种函数关系,如果你的两个自变量间(X1和X2)存在函数关系,那么X1改变一个单位时,X2也会相应地改变,此时你无法做到固定其他条件,单独考查X1对因变量Y的作用,你所观察到的X1的效应总是混杂了X2的作用,这就造成了分析误差,使得对自变量效应的分析不准确,所以做回归分析时需要排除高共线性的影响。
高共线性的存在可以通过几种不同的方式来确定:
- 尽管从理论上讲,该变量应该与Y高度相关,但回归系数并不显著。
- 添加或删除X特征变量时,回归系数会发生显着变化。
- X特征变量具有较高的成对相关性(pairwise correlations)(检查相关矩阵)。
标准线性回归的优化函数: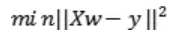
为了缓解这个问题,岭回归为变量增加了一个小的平方偏差因子(其实也就是正则项):
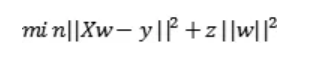
这种平方偏差因子向模型中引入少量偏差,但大大减少了方差。
岭回归的几个要点:
- 这种回归的假设与最小平方回归相同,不同点在于最小平方回归的时候,我们假设数据的误差服从高斯分布使用的是极大似然估计(MLE),在岭回归的时候,由于添加了偏差因子,即w的先验信息,使用的是**极大后验估计(MAP)**来得到最终参数的。
- 它缩小了系数的值,但没有达到零,这表明没有特征选择功能。
4 Lasso
4.1 基本原理及应用
Lasso使用L1 正则化。L1 正则化的结果是,使用 lasso 时某些系数刚好为 0 。这说明某些特征被模型完全忽略。这可以看作是一种自动化的特征选择。某些系数刚好为 0,这样模型更容易解释,也可以呈现模型最重要的特征。
from sklearn.linear_model import Lassolasso = Lasso().fit(X_train, y_train)
print(f'Train set score: {lasso.score(X_train, y_train)}')
print(f'Test set score: {lasso.score(X_test, y_test)}')
print(f'The number of feature: {np.sum(lasso.coef_ != 0)}')
[out]:
Train set score: 0.23918238514420065
Test set score: 0.2021552813955192
The number of feature: 3
4.2 Lasso调参
lasso001 = Lasso(alpha = 0.01, max_iter = 100000).fit(X_train, y_train)
print(f'Train set score: {lasso001.score(X_train, y_train)}')
print(f'Test set score: {lasso001.score(X_test, y_test)}')
print(f'The number of feature: {np.sum(lasso001.coef_ != 0)}')
[out]:
Train set score: 0.8557184508301234
Test set score: 0.9113857849877524
The number of feature: 36
lasso00001 = Lasso(alpha = 0.0001, max_iter = 100000).fit(X_train, y_train)
print(f'Train set score: {lasso00001.score(X_train, y_train)}')
print(f'Test set score: {lasso00001.score(X_test, y_test)}')
print(f'The number of feature: {np.sum(lasso00001.coef_ != 0)}')
[out]:
Train set score: 0.9272488231017324
Test set score: 0.9001399153473915
The number of feature: 91
plt.plot(lasso.coef_, 's', label = 'Lasso alpha = 1')
plt.plot(lasso001.coef_, '^', label = 'Lasso alpha = 0.01')
plt.plot(lasso00001.coef_, 'v', label = 'Lasso alpha = 0.0001')plt.plot(ridge01.coef_, 'o', label = 'Ridge alpha = 0.1')
plt.legend(ncol = 2, loc = (0, 1.05))
plt.ylim(-25, 25)
plt.xlabel('Coefficient index')
plt.xlabel('Coefficient magnitude')

4.3 为什么要用Lasso
总的来说,Lasso和Ridge类似,是为了减少共线性的影响,从而减少模型方差。
4.4 Lasso和Ridge的区别(L1,L2区别)
- 内置的特征选择(Built-in feature selection):这是L1范数的一个非常有用的属性,而L2范数不具有这种特性。这实际上因为是L1范数倾向于产生稀疏系数。例如,假设模型有100个系数,但其中只有10个系数是非零系数,这实际上是说“其他90个变量对预测目标值没有用处”。 而L2范数产生非稀疏系数,所以没有这个属性。因此,可以说Lasso回归做了一种“参数选择”形式,未被选中的特征变量对整体的权重为0。
- 稀疏性:指矩阵(或向量)中只有极少数条目非零。 L1范数具有产生具有零值或具有很少大系数的非常小值的许多系数的属性。
- 计算效率:L1范数没有解析解,但L2范数有。这使得L2范数的解可以通过计算得到。然而,L1范数的解具有稀疏性,这使得它可以与稀疏算法一起使用,这使得在计算上更有效率。
参考资料:https://mp.weixin.qq.com/s/mr83EK24S94b_UUlecyqlA
5 相关概念
5.1 模型偏差-模型方差
模型的偏差:训练出来的模型在训练集上的准确度。
模型的方差:模型是随机变量。设样本容量为n的训练集为随机变量的集合(X1, X2, …, Xn),那么模型是以这些随机变量为输入的随机变量函数(其本身仍然是随机变量):F(X1, X2, …, Xn)。抽样的随机性带来了模型的随机性。方差越大的模型越容易过拟合。
假设有两个训练集A和B,经过A训练的模型Fa与经过B训练的模型Fb差异很大,这意味着Fa在类A的样本集合上有更好的性能,而Fb在类B的训练样本集合上有更好的性能,这样导致在不同的训练集样本的条件下,训练得到的模型的效果差异性很大,很不稳定,这便是模型的过拟合现象。
而对于一些弱模型,它在不同的训练样本集上性能差异并不大,因此模型方差小,抗过拟合能力强,因此boosting算法就是基于弱模型来实现防止过拟合现象。
5.2 多重共线性相关
5.2.1 概念

5.2.2 影响
- 完全共线性下参数估计量不存在。
- 近似共线性下OLS估计精度较低。
参数的OLS估计量方差较大,其标准差也就较大,从而是的参数估计量精度较低。
- 参数估计量经济含义不合理。
我们进行回归分析需要了解每个自变量对因变量的单纯效应,多重共线性就是说自变量间存在某种函数关系,如果你的两个自变量间(X1和X2)存在函数关系,那么X1改变一个单位时,X2也会相应地改变,此时你无法做到固定其他条件,单独考查X1对因变量Y的作用,你所观察到的X1的效应总是混杂了X2的作用,这就造成了分析误差,使得对自变量效应的分析不准确,所以做回归分析时需要排除多重共线性的影响。
- 变量的显著性检验失去意义,可能将重要的解释变量排除在模型之外。
多重共线性,更容易接受F检验原假设(所有的参数均为0)因为R^2变大了,所以F值变大了。
更容易接受T检验原假设(参数不显著),是因为多重共线性的出现使得估计的参数方差变大,因此T值变小。
- 模型的预测功能失效。变大的方差容易使区间预测的“区间”变大,使预测失去意义。
需要注意:即使出现较高程度的多重共线性,OLS估计量仍具有线性性等良好的统计性质(仍然满足BLUE-最有线性无偏性,best,linear,unbiased,estimator)。但是OLS法在统计推断上无法给出真正有用的信息。
5.5.3 排除方法
- 排除引起共线性的变量。找出引起多重共线性的解释变量,将它排除出去,以逐步回归法得到最广泛的应用。
- 差分法。时间序列数据、线性模型:将原模型变换为差分模型。(还没看懂???)
- 减小参数估计量的方差:岭回归法(Ridge Regression)。
- 简单相关系数检验法。
参考资料:https://www.cnblogs.com/zongfa/p/9502470.html
参考资料:https://baike.baidu.com/item/%E5%A4%9A%E9%87%8D%E5%85%B1%E7%BA%BF%E6%80%A7/10201978?fr=aladdin









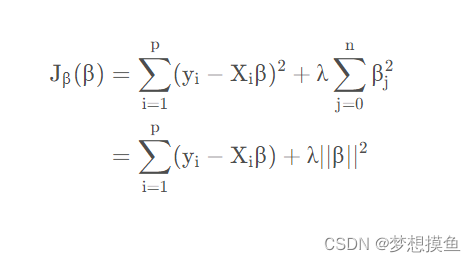


![[组原]初识-地址总线,地址寄存器,存储单元,存储字长](https://img-blog.csdnimg.cn/fec3f6f79ccb4139a78eac6fde3ece22.png)